© Владимир Каланов,"Знания-сила".
Явление приливов на море было замечено с самых древних времён. Геродот писал о приливах ещё в V веке до нашей эры. Природу приливов люди долгое время не могли понять. Высказывались различные фантастические предположения наподобие того, что Земля дышит. Даже знаменитый учёный И. Кеплер (1571-1630), открывший законы движения планет, рассматривал приливы и отливы как результат... дыхания планеты Земля.
Французский математик и философ Рене Декарт (1596-1650) первым среди европейских учёных указал на связь приливов с движением Луны, но не понял, в чём эта связь заключается. Поэтому дал такое далёкое от истины объяснение явлению прилива: Луна, вращаясь вокруг Земли, давит на воду, заставляя её понижаться.
Постепенно учёные разобрались в этой, надо сказать, непростой, проблеме, и было установлено, что приливы – это следствие воздействия гравитационных сил Луны и (в меньшей степени) Солнца на поверхность океана.
В океанологии дано следующее определение: ритмичные поднятия и опускания вод, а также сопровождающие их течения, называются приливами и отливами.
Приливы и отливы происходят не только в океане, но также в атмосфере и земной коре. Поднятие земной коры очень незначительны, поэтому их можно определить только специальными приборами. Другое дело – водная поверхность. Частицы воды движутся, и, получая со стороны Луны ускорение, приближаются к ней несравненно больше, чем земная твердь. Поэтому на стороне, обращённой к Луне, вода поднимается вверх, образуя изгиб, своеобразный водяной бугор на поверхности океана. Поскольку Земля вращается вокруг своей оси, этот водяной бугор перемещается по поверхности океана вслед за движением Луны.
Теоретически в образовании приливов участвуют даже далёкие звёзды. Но это остаётся чисто теоретическим посылом, так как воздействие звёзд ничтожно, и им можно пренебречь. Точнее даже, им невозможно пренебречь, так как нечем пренебрегать. Воздействие Солнца на поверхность океана из-за большой удалённости светила в 3-4 раза слабее воздействия Луны. Мощные лунные приливы маскируют притяжение Солнца и поэтому солнечных приливов как таковых не наблюдается.
Крайнее положение уровня воды в конце прилива называется полной водой, а в конце отлива – малой водой.
Две фотографии, сделанные с одной точки в моменты малой и полной воды,дают представление о приливных колебаниях уровня.
Если начать наблюдение за приливом в момент полной воды, то мы увидим, что через 6 часов наступит самое низкое стояние воды. После этого снова начнётся прилив, который также будет продолжаться 6 часов до достижения наивысшего уровня. Следующий прилив наступит через 24 часа после начала нашего наблюдения.
Но так будет происходить только в случае идеальных, теоретических условий. Реально в течение суток бывает по одной полной и малой воде – и тогда прилив называется суточным. А может успеть произойти в два приливных цикла. В этом случае речь идёт о полусуточном приливе.
Период суточного прилива продолжается не 24 часа, а на 50 минут дольше. Соответственно полусуточный прилив длится 12 часов 25 минут.
В Мировом океане происходят преимущественно полусуточные приливы. Объявляется это вращением Земли вокруг своей оси. Прилив, как огромная пологая волна длина которой составляет многие сотни километров, распространяется по всей поверхности Мирового океана. Период возникновения такой волны колеблется в каждом месте океане от половины суток до суток. По признаку периодичности наступления приливов их и различают как суточные и полусуточные.
За время полного оборота Земли вокруг своей оси Луна перемещается по небосводу примерно на 13 градусов. Чтобы «догнать», Луну, приливной волне как раз и требуется 50 минут. Это значит, что время прихода полной воды в одном и том же месте океана постоянно смещается относительно времени суток. Так, если сегодня полная вода была в полдень, то завтра она будет в 12 часов 50 минут, а послезавтра – в 13 часов 40 минут.
В открытом океане, где приливная волна не встречает сопротивления со стороны материков, островов, неровностей дна и береговой линии, имеют место в основном правильные полусуточные приливы. Приливные волны в открытом океане незаметны, там их высота не превышает одного метра.
В полную силу прилив проявляет себя на открытом побережье океана, где на десятки и сотни миль, не видно ни островов, ни резких изгибов береговой линии.
Когда Солнце и Луна располагаются на одной линии по одну сторону от Земли, сила притяжения обоих светил как бы складывается. Это бывает дважды в течение лунного месяца – в новолуние или полнолуние. Такое положение светил называется сизигием, а прилив, наступающий в эти дни, называется сизигийным. Сизигийные приливы – это самые высокие и мощные приливы. В отличие от них самые низкие приливы называются квадратурными .
Нужно отметить, что уровень сизигийных приливов в одном и том же месте не всегда одинаков. Причина всё та же: движение Луны вокруг - Земли и Земли – вокруг Солнца. Не забудем, что орбита Луны вокруг Земли – это не окружность, а эллипс, создающий достаточно ощутимую разницу между перигеем и апогеем Луны – 42 тысячи км. Если во время сизигия Луна будет находиться в перигее, то есть на наименьшем расстоянии от Земли, то это вызовет высокую приливную волну. Ну а если в этот же период Земля, двигаясь по своей эллиптической орбите вокруг Солнца, окажется на наименьшем от него расстоянии (а также совпадения изредка происходят), то приливы и отливы достигнут максимально большой величины.
Вот несколько примеров, показывающих максимальную высоту, которую достигают океанские приливы в отдельных местах земного шара (в метрах):
Название | Расположение | Высота прилива (м) |
Мезенский залив Белого моря | Россия | 10,0 |
Устье реки Колорадо | Мексика | 12,3 |
Пенжинская губа Охотского моря | Россия | 12,9 |
Устье реки Сеул | Южная Корея | 13,2 |
Устье реки Фицрой | Австралия | 14,0 |
Гренвилл | Ла-Манш | 14,7 |
Устье реки Коксоак | Канада | |
Порт Галлегас | Аргентина | 18,0 |
Залив Фанди | Канада | 19,6 |
Вода во время прилива поднимается с разной скоростью. Характер прилива в большой степени зависит от угла наклона морского дна. У крутых берегов вода поднимается сначала медленно – 8-10 миллиметров в минуту. Затем скорость прилива нарастает, становясь наибольшей к положению «вполводы». Потом она замедляется до положения верхней границы прилива. Динамика отлива аналогична динамике прилива. Но совсем по-иному выглядит прилив на широких пляжах. Здесь уровень воды нарастает очень быстро и иногда сопровождается высокой приливной волной, стремительно несущейся по отмели. Зазевавшимся на таких пляжах любителям купания в этих случаях ничего хорошего ожидать не приходится. Морская стихия шутить не умеет.
Во внутренние моря, отгороженные от остального океана узкими и мелкими извилистыми проливами или скоплениями небольших островов, приливы приходят с едва заметными амплитудами. Это мы видим на примере Балтийского моря, надёжно закрытого от приливов мелководными датскими проливами. Теоретически высота прилива в Балтийском море составляет 10 сантиметров. Но эти приливы на глаз незаметны, они скрываются колебаниями уровня воды от ветра или от изменений атмосферного давления.
Известно, что в Петербурге часто бывают наводнения, иногда очень сильные. Вспомним, как ярко и правдиво передал драму сильнейшего наводнения 1824 года в поэме «Медный всадник» великий русский поэт А.С. Пушкин. К счастью, наводнения такой силы в Петербурге никакого отношения к приливам не имеют. Эти наводнения вызываются ветрами циклонов, значительно, на 4–5 метров поднимающими уровень воды в восточной части Финского залива и в Неве.
Ещё меньше воздействуют океанские приливы на внутренние моря Чёрное и Азовское, а также Эгейское и Средиземное. В Азовском море, соединённом с Чёрным морем узким Керченским проливом, амплитуда приливов близка к нулю. В Чёрном море колебания уровня воды под влиянием приливов не достигают и 10 сантиметров.
И наоборот, в заливах и узких бухтах, имеющих свободное сообщение с океаном, приливы достигают значительной величины. Свободно входя в залив, приливные массы устремляются вперёд, и, не находя выхода среди суживающихся берегов, поднимаются вверх и заливают сушу на большой площади.
Во время океанских приливов в устьях некоторых рек наблюдается опасное явление, именуемое бором. Поток морской воды, войдя в русло реки и встретившись с речным потоком, образует мощный пенистый вал, встающий стеной и стремительно движущийся против течения реки. На своём пути бор размывает берега и может разрушить и потопить любое судно, если оно оказалось в фарватере реки.
На величайшей реке Южной Америки Амазонке мощная приливная волна высотой 5-6 метров проходит со скоростью 40–45 км/ч на расстояние до полутора тысяч километров от устья.
Иногда приливные волны останавливают течение рек и даже поворачивают его в обратную сторону.
На территории России небольшой по высоте бор испытывают реки, впадающие в Мезенский залив Белого моря.
С целью использования энергии приливов в некоторых странах, в том числе в России, построены приливные электростанции. Первая приливная электростанция, построенная в Кислогубской губе Белого моря, была мощностью всего 800 киловатт. В дальнейшем ПЭС проектировались уже мощностью в десятки и сотни тысяч киловатт. Это значит, что приливы начинают работать на пользу человеку.
И последнее, но зато глобально важное о приливах. Течения, вызываемые приливами, встречают сопротивление материков, островов и морского дна. Некоторые учёные считают, что в результате трения водных масс об указанные препятствия вращение Земли вокруг своей оси замедляется. На первый взгляд, это замедление совсем незначительное. Расчёты показали, что за всё время нашей эры, то есть за 2000 лет, сутки на Земле стали длиннее на 0,035 секунды. Но на чём основывался расчёт?
Оказывается, появились доказательства, хотя и косвенные, того, что вращение нашей планеты замедляется. Изучая вымершие кораллы девонского периода, английский учёный Д.Уэллс обнаружил, что количество суточных колец нарастания в 400 раз больше, чем годовых. В астрономии признана теория устойчивости планетных движений, по которой продолжительность года остаётся практически неизменной.
Получается, что в девонском периоде, то есть 380 млн. лет назад, год состоял из 400 суток. Следовательно, сутки тогда имели продолжительность 21 час 42 минуты.
Если Д.Уэллс не ошибся при подсчёте суточных колец древних кораллов, и если остальные расчёты верны, то всё идёт к тому, что не пройдёт и каких-нибудь 12–13 миллиардов лет, как земные сутки станут равными по продолжительности лунному месяцу. И что тогда? Тогда наша Земля будет постоянно обращена одной стороной к Луне, как это в настоящее время происходит с Луной по отношению к Земле. Поднятие воды стабилизируется на одной стороне Земли, приливы перестанут существовать, ну а солнечные приливы слишком слабы, чтобы быть ощутимыми.
Мы предоставляем возможность нашим читателям самостоятельно дать оценку этой достаточно экзотической гипотезе.
© Владимир Каланов,"Знания-сила"
znaniya-sila.narod.ru
ПРИЛИВЫ и ОТЛИВЫ — (Flood tide and ebb tide, ebb and flood) периодические изменения уровня воды в море, вызываемые действием на частицы воды сил притяжения Луны и Солнца и сил центробежных, возникающих от обращения систем Земля Луна, Земля Солнце вокруг их общих… … Морской словарь
приливы и отливы — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN tides and currents … Справочник технического переводчика
приливы и отливы — периодические колебания уровня океана (моря), обусловленные силами притяжения Луны и Солнца в соединении с центробежными силами, развивающимися при вращении систем Земля Луна и Земля Солнце. Большая из этих сил лунная определяет основные черты… … Морской биографический словарь
приливы и отливы — • приливы и отливы периодические колебания уровня Мирового океана, атмосферного давления и деформации твёрдого тела Земли, обусловленные силами притяжения Луны и Солнца. Под воздействием этих небесных тел возникают приливообразующие силы, которые … Географическая энциклопедия
приливы и отливы — potvyniai ir atoslūgiai statusas T sritis ekologija ir aplinkotyra apibrėžtis Periodiškas vandenynų vandens lygio svyravimas dėl Mėnulio ir Saulės traukos. Du kartus per parą vandenyno lygis pakyla – būna potvyniai ir du kartus per parą vėl… … Ekologijos terminų aiškinamasis žodynas
Приливы и отливы — периодические колебания уровня моря, атмосферного давления и деформации твёрдого тела Земли, обусловленные силами притяжения Луны и Солнца. Подробнее см. Приливы … Большая советская энциклопедия
Приливы и отливы — (франц. marées, нем. Gezeiten, англ. tides) периодические колебания уровня воды вследствие притяжения Луны и Солнца. Общие сведения. П. всего заметнее по берегам океанов. Тотчас после малой воды наибольшего отлива, уровень океана начинает… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРИЛИВЫ — ПРИЛИВЫ, периодический подъем и спад морской воды, вызванный силами притяжения Луны и, в меньшей степени, Солнца. На большей части территории Земли ежедневно происходит два прилива и два отлива. Каждый следующий прилив наступает через 12 часов и… … Научно-технический энциклопедический словарь
ОТЛИВЫ — (Ebb tide) см. Приливы и отливы. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
отливы — • приливы и отливы периодические колебания уровня Мирового океана, атмосферного давления и деформации твёрдого тела Земли, обусловленные силами притяжения Луны и Солнца. Под воздействием этих небесных тел возникают приливообразующие силы, которые … Географическая энциклопедия
dic.academic.ru
Прили́в и отли́в — периодические вертикальные колебания уровня океана или моря, являющиеся результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями данного рельефа и проявляющиеся в периодическом горизонтальном смещении водных масс. Приливы и отливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.
Интенсивность этих явлений зависит от многих факторов, однако наиболее важным из них является степень связи водоёмов с мировым океаном. Чем более замкнут водоём, тем меньше степень проявления приливо-отливных явлений.
Так, например, на побережье Финского залива эти явления заметны только на мелководье, а периодически происходившие ранее наводнения в Петербурге объяснялись длинной волной, связанной с колебаниями атмосферного давления и нагонными западными ветрами.
С другой стороны, если в месте образования прилива достаточно большой амплитуды имеется сужающийся залив или устье реки, это может привести к образованию мощной приливной волны, которая поднимается вверх по течению реки, иногда на сотни километров. Из таких волн наиболее известны:
Лунный интервал приливов — это период времени с момента прохождения Луны через точку зенита над вашей местностью до момента достижения наивысшего значения уровня воды во время прилива.
Хотя для земного шара величина силы тяготения Солнца почти в 200 раз больше, чем силы тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не от величины гравитационного поля, а от степени его неоднородности. При увеличении расстояния от источника поля неоднородность уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то приливные силы, вызываемые солнечным притяжением, оказываются слабее.
Также одной из причин возникновения приливов и отливов является суточное (собственное) вращение Земли. Массы воды мирового океана, имеющие форму эллипсоида, большая ось которого не совпадает с осью вращения Земли, участвуют в её вращении вокруг этой оси. Это ведёт к тому, что в системе отсчёта, связанной с земной поверхностью, по океану бегут по взаимно противоположным сторонам земного шара две волны, приводящие в каждой точке океанского побережья к периодическим, два раза в сутки повторяющимся явлениям отлива, чередующихся с приливами.
Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:
Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.
При объяснении причин приливов внимание обычно обращается лишь на второй из этих факторов. Но расхожее объяснение рассматриваемого явления только действием приливных сил неполно.
Приливная волна, имеющая форму упомянутого выше эллипсоида, представляет собой суперпозицию двух «двугорбых» волн, образовавшихся в результате гравитационного взаимодействия планетной пары Земля — Луна и гравитационного взаимодействия этой пары с центральным светилом — Солнцем с одной стороны. Кроме того, фактором, определяющим образование этой волны, выступают силы инерции[1], имеющие место при обращении небесных тел вокруг общих для них центров масс.
Ежегодно повторяющийся приливно-отливной цикл остаётся неизменным вследствие точной компенсации сил притяжения между Солнцем и центром масс планетной пары и силами инерции, приложенными к этому центру.
Поскольку положение Луны и Солнца по отношению к Земле периодически меняется, меняется и интенсивность результирующих приливно-отливных явлений.
Отлив у Сен-МалоГай Юлий Цезарь в книге "Записки о Галльской войне" (книга 4 гл. 29) связывает необычно высокий прилив у берегов Британии с наступившим новолунием, сообщая что до этого момента связь новолуния с высотой прилива римлянам не была известна.
Хосе де Акоста в своей Истории (1590) собрал доказательства связи отливов и приливов с фазами Луны: он указал, что период приливов, происходящих дважды в сутки, отличается на три четверти часа от солнечных суток, что известна также месячная периодичность приливов, а также добавил новое доказательство: приливы на обоих берегах Панамского перешейка происходят практически одновременно. Хосе де Акоста назвал приливы "одной из замечательных тайн Природы".[2].
Немецкий астроном Иоганн Кеплер, пришедший на основании своих наблюдений над планетами к идее всемирного тяготения, выдвинул гипотезу о том, что именно гравитация Луны является причиной приливов:
Когда Луна находится непосредственно над Атлантическим, так называемым Южным, Восточным или Индийским океаном, то она притягивает воды, омывающие земной шар. Не встречая на своем пути континентов, воды со всех сторон устремляются к обширному участку, находящемуся прямо под Луной, а берега при этом обнажаются. Но пока воды находятся в движении, Луна успевает переместиться и не располагается более прямо над океаном, в силу чего масса воды, бьющая в западный берег, перестает испытывать действие лунного притяжения и обрушивается на восточный берег. [3].
Не зная точного закона всемирного тяготения, Кеплер не смог создать количественную теорию приливов.
Отливы играли заметную роль в снабжении прибрежного населения морепродуктами, позволяя собирать на обнажившемся морском дне годную для еды пищу.
Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. В океане, где дно ровное, а суша далеко, полная вода проявляется как два «вздутия» водной поверхности: одно из них находится со стороны Луны, а другое — в противоположном конце земного шара. Также могут присутствовать ещё два меньших по размеру вздутия со стороны, направленной к Солнцу, и противоположной ему. Объяснение этому эффекту можно найти ниже, в разделе физика прилива .
Так как Луна и Солнце перемещаются относительно Земли, вместе с ними перемещаются и водные горбы, образуя прили́вные волны и прили́вные течения. В открытом море приливные течения имеют вращательный характер, а вблизи берегов и в узких заливах и проливах — возвратно-поступательный.
Если бы вся Земля была покрыта водой, мы бы наблюдали два регулярных прилива и отлива ежедневно. Но так как беспрепятственному распространению приливных волн мешают участки суши: острова и континенты, а также из-за действия силы Кориолиса на движущуюся воду, вместо двух приливных волн наблюдается множество маленьких волн, которые медленно (в большинстве случаев с периодом 12 ч 25,2 мин) обегают вокруг точки, называющейся амфидромической, в которой амплитуда прилива равна нулю. Доминирующая компонента прилива (лунный прилив М2) образует на поверхности Мирового океана около десятка амфидромических точек с движением волны по часовой стрелке и примерно столько же — против часовой (см. карту). Всё это делает невозможным предсказание времени прилива только на основе положений Луны и Солнца относительно Земли. Вместо этого используют «ежегодник приливов» — справочное пособие для вычисления времени наступления приливов и их высоты в различных пунктах земного шара. Также используются таблицы приливов, с данными о моментах и высотах малых и полных вод, вычисленными на год вперёд для основных прили́вных по́ртов.
Составляющая прилива M2Если соединить на карте точки с одинаковыми фазами прилива, мы получим так называемые котидальные линии, радиально расходящиеся из амфидромической точки. Обычно котидальные линии характеризуют положение гребня приливной волны для каждого часа. Фактически котидальные линии отражают скорость распространения приливной волны за 1 час. Карты, на которых представлены линии равных амплитуд и фаз приливных волн, называются котидальными картами.
Высота прилива — разница между высшим уровнем воды при приливе (полная вода) и низшим её уровнем при отливе (малая вода). Высота прилива — величина непостоянная, однако средний её показатель приводится при характеристике каждого участка побережья.
В зависимости от взаимного расположения Луны и Солнца малая и большая приливные волны могут усиливать друг друга. Для таких приливов исторически сложились специальные названия:
Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.
Высочайшие на Земле приливы (15,6—18 м) наблюдаются в бухте Фанди, которая находится на восточном побережье Канады между Нью-Брансуиком и Новой Шотландией. Примерно такие же приливы и в заливе Унгава на севере Квебека.
На Европейском континенте самые высокие приливы (до 13,5 м) наблюдаются в Бретани у города Сен-Мало. Здесь приливная волна фокусируется береговой чертой полуостровов Корнуолл (Англия) и Котантен (Франция).
В России самые высокие приливы случаются в Пенжинской губе Охотского моря — до 12,9 м. Это точка самых высоких приливов на всём Тихом океане.
Применительно к планете Земля приливной эффект является причиной смещения гравитационного поля Земли в сторону массы Луны.
(концепция акад. Шулейкина[4])
Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть r′{\displaystyle \mathbf {r} '} — радиус-вектор, направленный от пробного тела в сторону Луны, r′{\displaystyle r'} — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна
F=GMLr′3r′{\displaystyle \mathbf {F} ={\frac {G{{M}_{L}}}{r{{'}^{3}}}}\mathbf {r} '} (1)
где GML{\displaystyle G{{M}_{L}}} — селенометрическая гравитационная постоянная. Пробное тело поместим в точку P{\displaystyle P} . Сила притяжения пробного тела, помещённого в центр масс Земли будет равна
F0=GMLr3r{\displaystyle {{\mathbf {F} }_{0}}={\frac {G{{M}_{L}}}{{r}^{3}}}\mathbf {r} } (2)
Здесь под r{\displaystyle \mathbf {r} } и r{\displaystyle r} понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения
Ffl=F−F0{\displaystyle {{\mathbf {F} }_{fl}}=\mathbf {F} -{{\mathbf {F} }_{0}}} (3)
В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна GML╱r′{\displaystyle {}^{G{{M}_{L}}}\!\!\diagup \!\!{}_{r'}\;} Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось Ox{\displaystyle Ox} проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы F0{\displaystyle {{\mathbf {F} }_{0}}} будет равна GMLr2x+const{\displaystyle {\frac {G{{M}_{L}}}{{r}^{2}}}x+\operatorname {const} } . Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW{\displaystyle \delta W} , получим δW=GMLr′−GMLr2x−const{\displaystyle \delta W={\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-\operatorname {const} } Постоянную const{\displaystyle \operatorname {const} } определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли x=0{\displaystyle x=0} , r′=r{\displaystyle r'=r} Отсюда следует, что GMLr=const{\displaystyle {\frac {G{{M}_{L}}}{r}}=\operatorname {const} } . Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде
GMLr′−GMLr2x−GMLr{\displaystyle {\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-{\frac {G{{M}_{L}}}{r}}} (4)
Поскольку
r′=(r−x)2+y2+z2{\displaystyle r'={\sqrt {{{\left(r-x\right)}^{2}}+{{y}^{2}}+{{z}^{2}}}}}
то
1r′=1r[(1−xr)2+y2+z2r2]−12{\displaystyle {\frac {1}{r'}}={\frac {1}{r}}{{\left[{{\left(1-{\frac {x}{r}}\right)}^{2}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{r}^{2}}}\right]}^{-{\frac {1}{2}}}}}
При малых величинах x/r{\displaystyle {x}/{r}\;} , y/r{\displaystyle {y}/{r}\;} , z/r{\displaystyle {z}/{r}\;} , учитывая второй порядок малости, последнее выражение можно представить в следующем виде
1r′≈1r(1+xr+2x2−y2−z22r2){\displaystyle {\frac {1}{r'}}\approx {\frac {1}{r}}\left(1+{\frac {x}{r}}+{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)} (5)
Подставив (5) в (4), получим
δW=GML2x2−y2−z22r3{\displaystyle \delta W=G{{M}_{L}}{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}} (6)
Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен GMR{\displaystyle {\frac {GM}{R}}} . Для точки P{\displaystyle P} . , находящейся на расстоянии ρ{\displaystyle \rho } от центра сферы, гравитационный потенциал Земли равен GMρ{\displaystyle {\frac {GM}{\rho }}} . Сократив на гравитационную постоянную, получим 1ρ+MLM⋅2x2−y2−z22r3=1R{\displaystyle {\frac {1}{\rho }}+{\frac {{M}_{L}}{M}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}={\frac {1}{R}}} . Здесь переменными величинами являются x,y,z{\displaystyle x,y,z} и ρ{\displaystyle \rho } . Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой μ{\displaystyle \mu } и решим полученное выражение относительно ρ{\displaystyle \rho } :
ρ=R(1−μRr⋅2x2−y2−z22r2)−1≈R(1+μRr⋅2x2−y2−z22r2){\displaystyle \rho =R{{\left(1-\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}^{-1}}\approx R\left(1+\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}
Так как ρ2=x2+y2+z2{\displaystyle {{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}} с той же степенью точности получим
x2R2(1−2μR3r3)+y2+z2R2(1+μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{R}^{2}}}\left(1-2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)+{\frac {{{y}^{2}}+{{z}^{2}}}{{R}^{2}}}\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)=1}
Учитывая малость отношения R/r{\displaystyle {R}/{r}\;} последние выражения можно записать так
x2R2(1+2μR3r3)+y2+z2R2(1−μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{{R}^{2}}\left(1+2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left(1-\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}=1}
Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью Ox{\displaystyle Ox} , т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны
a=(1+μR3r3)R,b=c=(1−μR32r3)R{\displaystyle a=\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)R,\,\,\,b=c=\left(1-\mu {\frac {{R}^{3}}{2{{r}^{3}}}}\right)R}
Приведём в конце небольшую численную иллюстрацию данного эффекта. Вычислим приливные «горбы» на Земле, вызванные притяжением Луны и Солнца.
Радиус Земли равен R=6378{\displaystyle R=6378} км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты r=384,4⋅103{\displaystyle r=384,4\cdot {{10}^{3}}} км, отношение массы Земли к массе Луны равно 81:1 (μ=0,012345679{\displaystyle \mu =0,012345679} ). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.
Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное r=149,6⋅106{\displaystyle r=149,6\cdot {{10}^{6}}} км, и отношение массы Солнца к массе Земли μ=332982{\displaystyle \mu =332982} . В этом случае получаем величину «горба» около 16 см.
http-wikipediya.ru
Залив Фанди во время прилива и отлива. 
Прили́в и отли́в — периодические вертикальные колебания уровня океана или моря, являющиеся результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями данного рельефа и проявляющиеся в периодическом горизонтальном смещении водных масс. Приливы и отливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.
Интенсивность этих явлений зависит от многих факторов, однако наиболее важным из них является степень связи водоёмов с мировым океаном. Чем более замкнут водоём, тем меньше степень проявления приливо-отливных явлений.
Так, например, на побережье Финского залива эти явления заметны только на мелководье, а периодически происходившие ранее наводнения в Петербурге объяснялись длинной волной, связанной с колебаниями атмосферного давления и нагонными западными ветрами.
С другой стороны, если в месте образования прилива достаточно большой амплитуды имеется сужающийся залив или устье реки, это может привести к образованию мощной приливной волны, которая поднимается вверх по течению реки, иногда на сотни километров. Из таких волн наиболее известны:
Лунный интервал приливов — это период времени с момента прохождения Луны через точку зенита над вашей местностью до момента достижения наивысшего значения уровня воды во время прилива.
Хотя для земного шара величина силы тяготения Солнца почти в 200 раз больше, чем силы тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не от величины гравитационного поля, а от степени его неоднородности. При увеличении расстояния от источника поля неоднородность уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то приливные силы, вызываемые солнечным притяжением, оказываются слабее.
Также одной из причин возникновения приливов и отливов является суточное (собственное) вращение Земли. Массы воды мирового океана, имеющие форму эллипсоида, большая ось которого не совпадает с осью вращения Земли, участвуют в её вращении вокруг этой оси. Это ведёт к тому, что в системе отсчёта, связанной с земной поверхностью, по океану бегут по взаимно противоположным сторонам земного шара две волны, приводящие в каждой точке океанского побережья к периодическим, два раза в сутки повторяющимся явлениям отлива, чередующихся с приливами.
Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:
Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.
При объяснении причин приливов внимание обычно обращается лишь на второй из этих факторов. Но расхожее объяснение рассматриваемого явления только действием приливных сил неполно.
Приливная волна, имеющая форму упомянутого выше эллипсоида, представляет собой суперпозицию двух «двугорбых» волн, образовавшихся в результате гравитационного взаимодействия планетной пары Земля — Луна и гравитационного взаимодействия этой пары с центральным светилом — Солнцем с одной стороны. Кроме того, фактором, определяющим образование этой волны, выступают силы инерции[1], имеющие место при обращении небесных тел вокруг общих для них центров масс.
Ежегодно повторяющийся приливно-отливной цикл остаётся неизменным вследствие точной компенсации сил притяжения между Солнцем и центром масс планетной пары и силами инерции, приложенными к этому центру.
Поскольку положение Луны и Солнца по отношению к Земле периодически меняется, меняется и интенсивность результирующих приливно-отливных явлений.
Отлив у Сен-Мало Гай Юлий Цезарь в книге "Записки о Галльской войне" (книга 4 гл. 29) связывает необычно высокий прилив у берегов Британии с наступившим новолунием, сообщая что до этого момента связь новолуния с высотой прилива римлянам не была известна.
Хосе де Акоста в своей Истории (1590) собрал доказательства связи отливов и приливов с фазами Луны: он указал, что период приливов, происходящих дважды в сутки, отличается на три четверти часа от солнечных суток, что известна также месячная периодичность приливов, а также добавил новое доказательство: приливы на обоих берегах Панамского перешейка происходят практически одновременно. Хосе де Акоста назвал приливы "одной из замечательных тайн Природы".[2].
Немецкий астроном Иоганн Кеплер, пришедший на основании своих наблюдений над планетами к идее всемирного тяготения, выдвинул гипотезу о том, что именно гравитация Луны является причиной приливов:
Когда Луна находится непосредственно над Атлантическим, так называемым Южным, Восточным или Индийским океаном, то она притягивает воды, омывающие земной шар. Не встречая на своем пути континентов, воды со всех сторон устремляются к обширному участку, находящемуся прямо под Луной, а берега при этом обнажаются. Но пока воды находятся в движении, Луна успевает переместиться и не располагается более прямо над океаном, в силу чего масса воды, бьющая в западный берег, перестает испытывать действие лунного притяжения и обрушивается на восточный берег. [3].
Не зная точного закона всемирного тяготения, Кеплер не смог создать количественную теорию приливов.
Отливы играли заметную роль в снабжении прибрежного населения морепродуктами, позволяя собирать на обнажившемся морском дне годную для еды пищу.
Малая вода (Бретань, Франция) Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. В океане, где дно ровное, а суша далеко, полная вода проявляется как два «вздутия» водной поверхности: одно из них находится со стороны Луны, а другое — в противоположном конце земного шара. Также могут присутствовать ещё два меньших по размеру вздутия со стороны, направленной к Солнцу, и противоположной ему. Объяснение этому эффекту можно найти ниже, в разделе физика прилива
.
Так как Луна и Солнце перемещаются относительно Земли, вместе с ними перемещаются и водные горбы, образуя прили́вные волны и прили́вные течения. В открытом море приливные течения имеют вращательный характер, а вблизи берегов и в узких заливах и проливах — возвратно-поступательный.
Если бы вся Земля была покрыта водой, мы бы наблюдали два регулярных прилива и отлива ежедневно. Но так как беспрепятственному распространению приливных волн мешают участки суши: острова и континенты, а также из-за действия силы Кориолиса на движущуюся воду, вместо двух приливных волн наблюдается множество маленьких волн, которые медленно (в большинстве случаев с периодом 12 ч 25,2 мин) обегают вокруг точки, называющейся амфидромической, в которой амплитуда прилива равна нулю. Доминирующая компонента прилива (лунный прилив М2) образует на поверхности Мирового океана около десятка амфидромических точек с движением волны по часовой стрелке и примерно столько же — против часовой (см. карту). Всё это делает невозможным предсказание времени прилива только на основе положений Луны и Солнца относительно Земли. Вместо этого используют «ежегодник приливов» — справочное пособие для вычисления времени наступления приливов и их высоты в различных пунктах земного шара. Также используются таблицы приливов, с данными о моментах и высотах малых и полных вод, вычисленными на год вперёд для основных прили́вных по́ртов.
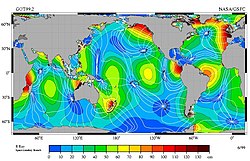Составляющая прилива M2 Если соединить на карте точки с одинаковыми фазами прилива, мы получим так называемые котидальные линии, радиально расходящиеся из амфидромической точки. Обычно котидальные линии характеризуют положение гребня приливной волны для каждого часа. Фактически котидальные линии отражают скорость распространения приливной волны за 1 час. Карты, на которых представлены линии равных амплитуд и фаз приливных волн, называются котидальными картами.
Высота прилива — разница между высшим уровнем воды при приливе (полная вода) и низшим её уровнем при отливе (малая вода). Высота прилива — величина непостоянная, однако средний её показатель приводится при характеристике каждого участка побережья.
В зависимости от взаимного расположения Луны и Солнца малая и большая приливные волны могут усиливать друг друга. Для таких приливов исторически сложились специальные названия:
Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.
Высочайшие на Земле приливы (15,6—18 м) наблюдаются в бухте Фанди, которая находится на восточном побережье Канады между Нью-Брансуиком и Новой Шотландией. Примерно такие же приливы и в заливе Унгава на севере Квебека.
На Европейском континенте самые высокие приливы (до 13,5 м) наблюдаются в Бретани у города Сен-Мало. Здесь приливная волна фокусируется береговой чертой полуостровов Корнуолл (Англия) и Котантен (Франция).
В России самые высокие приливы случаются в Пенжинской губе Охотского моря — до 12,9 м. Это точка самых высоких приливов на всём Тихом океане.
Применительно к планете Земля приливной эффект является причиной смещения гравитационного поля Земли в сторону массы Луны.
(концепция акад. Шулейкина[4])
Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть r′{\displaystyle \mathbf {r} '} — радиус-вектор, направленный от пробного тела в сторону Луны, r′{\displaystyle r'} — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна
F=GMLr′3r′,{\displaystyle \mathbf {F} ={\frac {G{{M}_{L}}}{r{{'}^{3}}}}\mathbf {r} ',\quad } (1)где GML{\displaystyle G{{M}_{L}}} — селенометрическая гравитационная постоянная. Пробное тело поместим в точку P{\displaystyle P}. Сила притяжения пробного тела, помещённого в центр масс Земли будет равна
F0=GMLr3r.(2){\displaystyle {{\mathbf {F} }_{0}}={\frac {G{{M}_{L}}}{{r}^{3}}}\mathbf {r} .\quad (2)}Здесь под r{\displaystyle \mathbf {r} } и r{\displaystyle r} понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения
Ffl=F−F0.(3){\displaystyle {{\mathbf {F} }_{fl}}=\mathbf {F} -{{\mathbf {F} }_{0}}.\quad (3)}В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна GML╱r′{\displaystyle {}^{G{{M}_{L}}}\!\!\diagup \!\!{}_{r'}\;} Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось Ox{\displaystyle Ox} проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы F0{\displaystyle {{\mathbf {F} }_{0}}} будет равна GMLr2x+const{\displaystyle {\frac {G{{M}_{L}}}{{r}^{2}}}x+\operatorname {const} }. Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW{\displaystyle \delta W}, получим
δW=GMLr′−GMLr2x−const.{\displaystyle \delta W={\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-\operatorname {const} .}Постоянную const{\displaystyle \operatorname {const} } определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли
x=0,{\displaystyle x=0,} r′=r.{\displaystyle r'=r.}Отсюда следует, что
GMLr=const.{\displaystyle {\frac {G{{M}_{L}}}{r}}=\operatorname {const} .}Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде
GMLr′−GMLr2x−GMLr.(4){\displaystyle {\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-{\frac {G{{M}_{L}}}{r}}.\quad (4)}Поскольку
r′=(r−x)2+y2+z2,{\displaystyle r'={\sqrt {{{\left(r-x\right)}^{2}}+{{y}^{2}}+{{z}^{2}}}},}то
1r′=1r[(1−xr)2+y2+z2r2]−12.{\displaystyle {\frac {1}{r'}}={\frac {1}{r}}{{\left[{{\left(1-{\frac {x}{r}}\right)}^{2}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{r}^{2}}}\right]}^{-{\frac {1}{2}}}}.}При малых величинах x/r{\displaystyle {x}/{r}\;}, y/r{\displaystyle {y}/{r}\;}, z/r{\displaystyle {z}/{r}\;}, учитывая второй порядок малости, последнее выражение можно представить в следующем виде
1r′≈1r(1+xr+2x2−y2−z22r2).(5){\displaystyle {\frac {1}{r'}}\approx {\frac {1}{r}}\left(1+{\frac {x}{r}}+{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right).\quad (5)}Подставив (5) в (4), получим
δW=GML2x2−y2−z22r3.(6){\displaystyle \delta W=G{{M}_{L}}{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}.\quad (6)}Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен
GMR.{\displaystyle {\frac {GM}{R}}.}Для точки P,{\displaystyle P,} находящейся на расстоянии ρ{\displaystyle \rho } от центра сферы, гравитационный потенциал Земли равен
GMρ.{\displaystyle {\frac {GM}{\rho }}.}Сократив на гравитационную постоянную, получим
1ρ+MLM⋅2x2−y2−z22r3=1R.{\displaystyle {\frac {1}{\rho }}+{\frac {{M}_{L}}{M}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}={\frac {1}{R}}.}Здесь переменными величинами являются: x,y,z{\displaystyle x,y,z} и ρ.{\displaystyle \rho .} Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой: μ{\displaystyle \mu } и решим полученное выражение относительно ρ{\displaystyle \rho }:
ρ=R(1−μRr⋅2x2−y2−z22r2)−1≈R(1+μRr⋅2x2−y2−z22r2).{\displaystyle \rho =R{{\left(1-\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}^{-1}}\approx R\left(1+\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right).}Так как
ρ2=x2+y2+z2{\displaystyle {{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}}с той же степенью точности получим
x2R2(1−2μR3r3)+y2+z2R2(1+μR3r3)=1.{\displaystyle {\frac {{x}^{2}}{{R}^{2}}}\left(1-2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)+{\frac {{{y}^{2}}+{{z}^{2}}}{{R}^{2}}}\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)=1.}Учитывая малость отношения R/r{\displaystyle {R}/{r}\;} последние выражения можно записать так
x2R2(1+2μR3r3)+y2+z2R2(1−μR3r3)=1.{\displaystyle {\frac {{x}^{2}}{{{R}^{2}}\left(1+2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left(1-\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}=1.}Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью Ox{\displaystyle Ox}, то есть с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны
a=(1+μR3r3)R,b=c=(1−μR32r3)R.{\displaystyle a=\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)R,\,\,\,b=c=\left(1-\mu {\frac {{R}^{3}}{2{{r}^{3}}}}\right)R.}Приведём в конце небольшую численную иллюстрацию данного эффекта. Вычислим приливные «горбы» на Земле, вызванные притяжением Луны и Солнца.
Радиус Земли равен R=6378{\displaystyle R=6378} км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты r=384,4⋅103{\displaystyle r=384,4\cdot {{10}^{3}}} км, отношение массы Земли к массе Луны равно 81:1 (μ=0,012345679{\displaystyle \mu =0,012345679}). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.
Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное r=149,6⋅106{\displaystyle r=149,6\cdot {{10}^{6}}} км, и отношение массы Солнца к массе Земли μ=332982{\displaystyle \mu =332982}. В этом случае получаем величину «горба» около 16 см.
www.gpedia.com
Прили́в и отли́в — периодические вертикальные колебания уровня океана или моря, являющиеся результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями данного рельефа и проявляющиеся в периодическом горизонтальном смещении водных масс. Приливы и отливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.
Интенсивность этих явлений зависит от многих факторов, однако наиболее важным из них является степень связи водоёмов с мировым океаном. Чем более замкнут водоём, тем меньше степень проявления приливо-отливных явлений.
Так, например, на побережье Финского залива эти явления заметны только на мелководье, а периодически происходившие ранее наводнения в Петербурге объяснялись длинной волной, связанной с колебаниями атмосферного давления и нагонными западными ветрами.
С другой стороны, если в месте образования прилива достаточно большой амплитуды имеется сужающийся залив или устье реки, это может привести к образованию мощной приливной волны, которая поднимается вверх по течению реки, иногда на сотни километров. Из таких волн наиболее известны:
Лунный интервал приливов — это период времени с момента прохождения Луны через точку зенита над вашей местностью до момента достижения наивысшего значения уровня воды во время прилива.
Хотя для земного шара величина силы тяготения Солнца почти в 200 раз больше, чем силы тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не от величины гравитационного поля, а от степени его неоднородности. При увеличении расстояния от источника поля неоднородность уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то приливные силы, вызываемые солнечным притяжением, оказываются слабее.
Также одной из причин возникновения приливов и отливов является суточное (собственное) вращение Земли. Массы воды мирового океана, имеющие форму эллипсоида, большая ось которого не совпадает с осью вращения Земли, участвуют в её вращении вокруг этой оси. Это ведёт к тому, что в системе отсчёта, связанной с земной поверхностью, по океану бегут по взаимно противоположным сторонам земного шара две волны, приводящие в каждой точке океанского побережья к периодическим, два раза в сутки повторяющимся явлениям отлива, чередующихся с приливами.
Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:
Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.
При объяснении причин приливов внимание обычно обращается лишь на второй из этих факторов. Но расхожее объяснение рассматриваемого явления только действием приливных сил неполно.
Приливная волна, имеющая форму упомянутого выше эллипсоида, представляет собой суперпозицию двух «двугорбых» волн, образовавшихся в результате гравитационного взаимодействия планетной пары Земля — Луна и гравитационного взаимодействия этой пары с центральным светилом — Солнцем с одной стороны. Кроме того, фактором, определяющим образование этой волны, выступают силы инерции[1], имеющие место при обращении небесных тел вокруг общих для них центров масс.
Ежегодно повторяющийся приливно-отливной цикл остаётся неизменным вследствие точной компенсации сил притяжения между Солнцем и центром масс планетной пары и силами инерции, приложенными к этому центру.
Поскольку положение Луны и Солнца по отношению к Земле периодически меняется, меняется и интенсивность результирующих приливно-отливных явлений.
Отлив у Сен-МалоГай Юлий Цезарь в книге "Записки о Галльской войне" (книга 4 гл. 29) связывает необычно высокий прилив у берегов Британии с наступившим новолунием, сообщая что до этого момента связь новолуния с высотой прилива римлянам не была известна.
Хосе де Акоста в своей Истории (1590) собрал доказательства связи отливов и приливов с фазами Луны: он указал, что период приливов, происходящих дважды в сутки, отличается на три четверти часа от солнечных суток, что известна также месячная периодичность приливов, а также добавил новое доказательство: приливы на обоих берегах Панамского перешейка происходят практически одновременно. Хосе де Акоста назвал приливы "одной из замечательных тайн Природы".[2].
Немецкий астроном Иоганн Кеплер, пришедший на основании своих наблюдений над планетами к идее всемирного тяготения, выдвинул гипотезу о том, что именно гравитация Луны является причиной приливов:
Когда Луна находится непосредственно над Атлантическим, так называемым Южным, Восточным или Индийским океаном, то она притягивает воды, омывающие земной шар. Не встречая на своем пути континентов, воды со всех сторон устремляются к обширному участку, находящемуся прямо под Луной, а берега при этом обнажаются. Но пока воды находятся в движении, Луна успевает переместиться и не располагается более прямо над океаном, в силу чего масса воды, бьющая в западный берег, перестает испытывать действие лунного притяжения и обрушивается на восточный берег. [3].
Не зная точного закона всемирного тяготения, Кеплер не смог создать количественную теорию приливов.
Отливы играли заметную роль в снабжении прибрежного населения морепродуктами, позволяя собирать на обнажившемся морском дне годную для еды пищу.
Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. В океане, где дно ровное, а суша далеко, полная вода проявляется как два «вздутия» водной поверхности: одно из них находится со стороны Луны, а другое — в противоположном конце земного шара. Также могут присутствовать ещё два меньших по размеру вздутия со стороны, направленной к Солнцу, и противоположной ему. Объяснение этому эффекту можно найти ниже, в разделе физика прилива .
Так как Луна и Солнце перемещаются относительно Земли, вместе с ними перемещаются и водные горбы, образуя прили́вные волны и прили́вные течения. В открытом море приливные течения имеют вращательный характер, а вблизи берегов и в узких заливах и проливах — возвратно-поступательный.
Если бы вся Земля была покрыта водой, мы бы наблюдали два регулярных прилива и отлива ежедневно. Но так как беспрепятственному распространению приливных волн мешают участки суши: острова и континенты, а также из-за действия силы Кориолиса на движущуюся воду, вместо двух приливных волн наблюдается множество маленьких волн, которые медленно (в большинстве случаев с периодом 12 ч 25,2 мин) обегают вокруг точки, называющейся амфидромической, в которой амплитуда прилива равна нулю. Доминирующая компонента прилива (лунный прилив М2) образует на поверхности Мирового океана около десятка амфидромических точек с движением волны по часовой стрелке и примерно столько же — против часовой (см. карту). Всё это делает невозможным предсказание времени прилива только на основе положений Луны и Солнца относительно Земли. Вместо этого используют «ежегодник приливов» — справочное пособие для вычисления времени наступления приливов и их высоты в различных пунктах земного шара. Также используются таблицы приливов, с данными о моментах и высотах малых и полных вод, вычисленными на год вперёд для основных прили́вных по́ртов.
Составляющая прилива M2Если соединить на карте точки с одинаковыми фазами прилива, мы получим так называемые котидальные линии, радиально расходящиеся из амфидромической точки. Обычно котидальные линии характеризуют положение гребня приливной волны для каждого часа. Фактически котидальные линии отражают скорость распространения приливной волны за 1 час. Карты, на которых представлены линии равных амплитуд и фаз приливных волн, называются котидальными картами.
Высота прилива — разница между высшим уровнем воды при приливе (полная вода) и низшим её уровнем при отливе (малая вода). Высота прилива — величина непостоянная, однако средний её показатель приводится при характеристике каждого участка побережья.
В зависимости от взаимного расположения Луны и Солнца малая и большая приливные волны могут усиливать друг друга. Для таких приливов исторически сложились специальные названия:
Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.
Высочайшие на Земле приливы (15,6—18 м) наблюдаются в бухте Фанди, которая находится на восточном побережье Канады между Нью-Брансуиком и Новой Шотландией. Примерно такие же приливы и в заливе Унгава на севере Квебека.
На Европейском континенте самые высокие приливы (до 13,5 м) наблюдаются в Бретани у города Сен-Мало. Здесь приливная волна фокусируется береговой чертой полуостровов Корнуолл (Англия) и Котантен (Франция).
В России самые высокие приливы случаются в Пенжинской губе Охотского моря — до 12,9 м. Это точка самых высоких приливов на всём Тихом океане.
Применительно к планете Земля приливной эффект является причиной смещения гравитационного поля Земли в сторону массы Луны.
(концепция акад. Шулейкина[4])
Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть r′{\displaystyle \mathbf {r} '} — радиус-вектор, направленный от пробного тела в сторону Луны, r′{\displaystyle r'} — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна
F=GMLr′3r′{\displaystyle \mathbf {F} ={\frac {G{{M}_{L}}}{r{{'}^{3}}}}\mathbf {r} '} (1)
где GML{\displaystyle G{{M}_{L}}} — селенометрическая гравитационная постоянная. Пробное тело поместим в точку P{\displaystyle P} . Сила притяжения пробного тела, помещённого в центр масс Земли будет равна
F0=GMLr3r{\displaystyle {{\mathbf {F} }_{0}}={\frac {G{{M}_{L}}}{{r}^{3}}}\mathbf {r} } (2)
Здесь под r{\displaystyle \mathbf {r} } и r{\displaystyle r} понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения
Ffl=F−F0{\displaystyle {{\mathbf {F} }_{fl}}=\mathbf {F} -{{\mathbf {F} }_{0}}} (3)
В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна GML╱r′{\displaystyle {}^{G{{M}_{L}}}\!\!\diagup \!\!{}_{r'}\;} Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось Ox{\displaystyle Ox} проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы F0{\displaystyle {{\mathbf {F} }_{0}}} будет равна GMLr2x+const{\displaystyle {\frac {G{{M}_{L}}}{{r}^{2}}}x+\operatorname {const} } . Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW{\displaystyle \delta W} , получим δW=GMLr′−GMLr2x−const{\displaystyle \delta W={\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-\operatorname {const} } Постоянную const{\displaystyle \operatorname {const} } определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли x=0{\displaystyle x=0} , r′=r{\displaystyle r'=r} Отсюда следует, что GMLr=const{\displaystyle {\frac {G{{M}_{L}}}{r}}=\operatorname {const} } . Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде
GMLr′−GMLr2x−GMLr{\displaystyle {\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-{\frac {G{{M}_{L}}}{r}}} (4)
Поскольку
r′=(r−x)2+y2+z2{\displaystyle r'={\sqrt {{{\left(r-x\right)}^{2}}+{{y}^{2}}+{{z}^{2}}}}}
то
1r′=1r[(1−xr)2+y2+z2r2]−12{\displaystyle {\frac {1}{r'}}={\frac {1}{r}}{{\left[{{\left(1-{\frac {x}{r}}\right)}^{2}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{r}^{2}}}\right]}^{-{\frac {1}{2}}}}}
При малых величинах x/r{\displaystyle {x}/{r}\;} , y/r{\displaystyle {y}/{r}\;} , z/r{\displaystyle {z}/{r}\;} , учитывая второй порядок малости, последнее выражение можно представить в следующем виде
1r′≈1r(1+xr+2x2−y2−z22r2){\displaystyle {\frac {1}{r'}}\approx {\frac {1}{r}}\left(1+{\frac {x}{r}}+{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)} (5)
Подставив (5) в (4), получим
δW=GML2x2−y2−z22r3{\displaystyle \delta W=G{{M}_{L}}{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}} (6)
Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен GMR{\displaystyle {\frac {GM}{R}}} . Для точки P{\displaystyle P} . , находящейся на расстоянии ρ{\displaystyle \rho } от центра сферы, гравитационный потенциал Земли равен GMρ{\displaystyle {\frac {GM}{\rho }}} . Сократив на гравитационную постоянную, получим 1ρ+MLM⋅2x2−y2−z22r3=1R{\displaystyle {\frac {1}{\rho }}+{\frac {{M}_{L}}{M}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}={\frac {1}{R}}} . Здесь переменными величинами являются x,y,z{\displaystyle x,y,z} и ρ{\displaystyle \rho } . Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой μ{\displaystyle \mu } и решим полученное выражение относительно ρ{\displaystyle \rho } :
ρ=R(1−μRr⋅2x2−y2−z22r2)−1≈R(1+μRr⋅2x2−y2−z22r2){\displaystyle \rho =R{{\left(1-\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}^{-1}}\approx R\left(1+\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}
Так как ρ2=x2+y2+z2{\displaystyle {{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}} с той же степенью точности получим
x2R2(1−2μR3r3)+y2+z2R2(1+μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{R}^{2}}}\left(1-2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)+{\frac {{{y}^{2}}+{{z}^{2}}}{{R}^{2}}}\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)=1}
Учитывая малость отношения R/r{\displaystyle {R}/{r}\;} последние выражения можно записать так
x2R2(1+2μR3r3)+y2+z2R2(1−μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{{R}^{2}}\left(1+2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left(1-\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}=1}
Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью Ox{\displaystyle Ox} , т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны
a=(1+μR3r3)R,b=c=(1−μR32r3)R{\displaystyle a=\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)R,\,\,\,b=c=\left(1-\mu {\frac {{R}^{3}}{2{{r}^{3}}}}\right)R}
Приведём в конце небольшую численную иллюстрацию данного эффекта. Вычислим приливные «горбы» на Земле, вызванные притяжением Луны и Солнца.
Радиус Земли равен R=6378{\displaystyle R=6378} км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты r=384,4⋅103{\displaystyle r=384,4\cdot {{10}^{3}}} км, отношение массы Земли к массе Луны равно 81:1 (μ=0,012345679{\displaystyle \mu =0,012345679} ). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.
Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное r=149,6⋅106{\displaystyle r=149,6\cdot {{10}^{6}}} км, и отношение массы Солнца к массе Земли μ=332982{\displaystyle \mu =332982} . В этом случае получаем величину «горба» около 16 см.
www-wikipediya.ru
Ты, конечно, слышал, что существует всемирное тяготение — взаимное ПРИТЯЖЕНИЕ между всеми звёздами и планетами. Оно было открыто великим английским учёным Исааком НЬЮТОНОМ. Лунное притяжение ощущается на Земле сильнее солнечного, потому что Луна хотя и гораздо меньше Солнца, но при этом в 390 раз ближе к нашей планете.
Лунное притяжение с одинаковой силой действует на все части Земли. Но влияние его на атмосферу и на сушу можно обнаружить лишь с помощью очень чувствительных приборов. А вот изменения в морях и океанах очень заметны. На той стороне Земли, против которой находится в это время Луна, вода как бы вспухает, образуя гигантский пологий вал. Он следует за Луной вокруг всего земного шара. В открытом море его не заметишь, он обнаруживает себя лишь в тот момент, когда на пути волны оказываются острова или материки. Набегая на берег, вода его заливает. Это и есть прилив.
Понятно, что когда вода, следуя за Луной, поднимается в одном месте, ее уровень в другом должен понижаться. Там происходит отлив, во время которого ранее затопленные приливом берега вновь обнажаются. Обычно приливы и отливы на побережье сменяют друг друга два раза в сутки.
— А почему два?—спросишь ты.— Ведь Луна обходит Землю за сутки всего один раз!
Верно! Но дело в том, что приливная волна зависит не только от лунного притяжения, но и от солнечного, и от того, что Земля всё время вращается. Вот в результате сложения и взаимодействия всех этих сил в большинстве мест земного шара приливы и отливы сменяют друг друга через каждые 6 часов.
Величина прилива зависит от разных причин: от размеров суши, на которую наталкивается приливная волна, от глубины и формы морского дна, от того, низок или высок сам берег.
Самые большие приливы, достигающие высоты почти 18 м, бывают у северовосточных берегов Канады, в заливе Фанди. Рыбаки развешивают там сети на жердях прямо на берегу. Во время прилива сети скрываются под воду и в них попадает рыба.
Сила прилива бывает иной раз так велика, что заставляет некоторые реки, например могучую Амазонку, течь вспять — от устья к верховьям.
Учёные разных стран заняты сейчас созданием специальных турбин, которые будет вращать энергия приливов и отливов, давая дешёвый электрический ток.
27 августа 1883 года огромное извержение вулкана практически уничтожило остров Кракатау. Этот взрыв образовал волны высотой несколько десятков метров, которые стерли с лица Земли сотни деревень. Волны пронеслись по океану со скоростью до 1300 км/час, достигнув берегов Австралии и Калифорнии за многие тысячи километров от места катастрофы!
В 1946 году в районе Алеутских островов произошло подводное землетрясение. Образовавшаяся гигантская волна менее чем за пять часов, преодолев почти 4 тыс. км, обрушилась на Гавайи. Она разрушила дома и мосты на расстоянии сотен метров от берега. Погибло 170 человек.
Такие волны называются приливными. Они совершенно не похожи на обычные волны в море или у берега и не зависят ни от ветра, ни от течения. Ученые дали этим волнам японское название «цунами». Различные катаклизмы, происходящие на морском дне, создают приливные волны, или цунами. Как правило, это подводные землетрясения.
В результате подводного землетрясения образуется ударная волна, которая распространяется в воде наподобие того, как звук распространяется в воздухе. И действительно, такая ударная волна в воде имеет скорость звука.
Если в этом районе окажется корабль, он ощутит на себе силу ударной волны, а это примерно то же самое, что и столкновение корабля со скалой!
При подводном землетрясении происходит перемещение морского дна по вертикали и горизонтали. Вот эти перемещения дна и ударная волна вызывают приливные волны. На поверхности воды может внезапно образоваться огромная воронка или наоборот — возникает столб воды. Появляется приливная волна, которая с огромной скоростью движется по морской поверхности.
Когда приливная волна приближается к берегу, ее первым признаком, как ни странно, может быть незначительное повышение уровня моря. Затем на несколько минут море отступает, как при отливе. Может обнажиться обширный участок морского дна. И затем появляется всеразрушающая приливная волна!
www.what-who.com
Приливы и отливы — периодические повышения и понижения уровня воды в океанах и морях. Дважды в течение суток с промежутком около 12 ч 25 мин вода у берега океана или открытого моря поднимается и, если нет преград, заливает иногда большие пространства — происходит прилив, а затем понижается и отступает, обнажая дно, — происходит отлив. Еще в древние времена люди связывали приливы и отливы с Луной. И действительно, основная причина приливов, как впервые указал И. Ньютон, — это притяжение Земли Луной, точнее говоря, разность между притяжением Луной всей Земли в целом, с одной стороны, и водной оболочки ее — с другой.
Теория Ньютона объясняет приливы и отливы следующим образом. Притяжение Земли Луной складывается из притяжения Луной отдельных частиц Земли. Частицы, находящиеся в данный момент ближе к Луне, притягиваются ею сильнее, а более далекие — слабее. Если бы Земля была абсолютно твердой, то это различие в силе притяжения не играло бы никакой роли. Но Земля не абсолютно твердое тело. Поэтому разность сил притяжения частиц, находящихся вблизи поверхности Земли и вблизи ее центра (эту разность называют приливообразующей силой), смещает частицы друг относительно друга, и Земля, прежде всего ее водная оболочка, деформируется.
В результате на стороне Земли, обращенной к Луне, и на противоположной стороне (точки А и В) вода поднимается, образуя приливные выступы, и там накапливается излишек воды. За счет этого уровень воды в точках С и D Земли в это время снижается — здесь наступает отлив (см. рис.).
Приливные выступы стремятся сохранить по отношению к Луне одно и то же положение, и если бы Земля не вращалась, а Луна оставалась неподвижной, то Земля вместе со своей водной оболочкой всегда сохраняла бы одну и ту же вытянутую форму. Однако Земля вращается, а Луна движется вокруг Земли примерно за 24 ч 50 мин. С этим же периодом приливные выступы следуют за Луной и перемещаются по поверхности океанов и морей с востока на запад. Поскольку таких выступов два, над каждым пунктом в океане дважды в сутки с интервалом около 12 ч 25 мин проходит приливная волна.
В открытом океане вода поднимается при прохождении приливной волны незначительно (примерно на 1 м и менее), что остается практически незаметным для мореплавателей. Но у берегов даже такой подъем уровня воды заметен. В бухтах и узких заливах уровень воды поднимается во время приливов гораздо выше, так как берег препятствует движению приливной волны, и вода накапливается здесь в течение всего времени между отливом и приливом. Самый большой прилив (около 18 м) наблюдается в одной из бухт на побережье Канады. В СССР наибольшие приливы (около 13 м) происходят в Гижигинской и Пенжинской губах Охотского моря. Во внутренних морях, например в Балтийском и Черном, приливы и отливы почти незаметны, поскольку в такие моря не успевают проникнуть массы воды, перемещающиеся вместе с океанской приливной волной. Правда, в каждом закрытом море или даже озере возникают самостоятельные приливные волны, но они несут с собой относительно небольшие массы воды. Высота приливов в Черном море достигает лишь 10 см.
В одной и той же местности высота прилива непостоянна, так как расстояние от Луны до Земли и наибольшая высота Луны над горизонтом с течением времени не остаются неизменными, а это приводит к изменению величины приливообразующих сил. В частности, изменение расстояния от Луны до Земли в течение месяца от 363 тыс. км до 406 тыс. км приводит к изменению этих сил в 1,25 раза.
Заметное приливное действие оказывает также и Солнце. Подсчитано, что в среднем приливные силы Солнца меньше приливных сил Луны в 2,2 раза.
Во время новолуния и полнолуния приливные силы Солнца и Луны действуют в одном направлении, и получаются наиболее высокие приливы. Во время же первой и третьей четвертей Луны приливные силы Солнца и Луны как бы противодействуют одна другой, и приливы бывают значительно меньшими. Во многих странах издаются «Таблицы приливов», где указана высота прилива в различных портах на каждый час в течение всех дней в году.
Приливные явления происходят не только в водной, но и в воздушной оболочке Земли (атмосферные приливы и отливы), а также в твердом теле Земли (поскольку Земля не является абсолютно твердой). Вертикальные колебания поверхности Земли вследствие приливов достигают нескольких десятков сантиметров.
Вполне перспективным является строительство приливных электростанций, в которых перемещающиеся во время приливов и отливов массы воды вращают колеса турбин. В 1967 г. во Франции пущена в эксплуатацию приливная электростанция в устье реки Ране. В 1968 г. дала ток опытная приливная электростанция, построенная в СССР в Кислой губе близ Мурманска. Проектируется в будущем строительство других приливных электростанций.
yunc.org
|
|
|
|
|
|
