Прилив и отлив моря. Отлив и прилив

Прилив и отлив моря

Кто не хотел бы совершить прогулку на дно моря? «Это невозможно! — воскликнете вы. — Для этого нужен хотя бы кессон!» Но разве вы не знаете, что два раза в сутки открываются для обозрения большие пространства морского дна? Правда, горе тому, кто вздумает задержаться на этой «выставке» сверх установленного времени! Морское дно открывается при отливе. Прилив и отлив моря — это смена высокой и низкой воды.

Прилив и отлив моря

Это одна из загадок природы. Ее пытались решить многие естествоиспытатели: Кеплер, открывший закон движения планет, Ньютон, установивший основные законы движения, французский ученый Лаплас, изучавший возникновение небесных тел. Все они хотели проникнуть в тайны жизни океанов.

Ветер создает волны на море. Но, чтобы управлять приливом и отливом, ветер слишком слаб. Даже шторм может быть только помощником при приливе. Какие же исполинские силы выполняют такую тяжелую работу?

Влияние Луны на приливы и отливы

Три исполина борются за мировой океан: Солнце, Луна и сама Земля. Солнце сильнее всех, но оно слишком далеко от нас, чтобы быть победителем. Движением масс воды на Земле управляет в основном Луна. Находясь на расстоянии 384 000 километров от Земли, она регулирует «пульс» океанов. Подобно огромному магниту, Луна притягивает массы воды на несколько метров вверх, в то время как Земля вращается вокруг своей оси.

Хотя разница между высотой прилива и отлива в среднем не больше 4 метров, работа, которую при этом выполняет Луна, огромна. Она равна 11 триллионам лошадиных сил. Если это число написать одними цифрами, то оно будет иметь 18 нулей и выглядеть так: 11 000 000 000 000 000 000. Такого количества лошадей не собрать, даже если согнать табуны со всех «концов» земного шара.

Приливы и отливы — источники энергии

После Солнца приливы и отливы — самые большие источники энергии. Они могли бы дать электрический ток всему миру. С незапамятных времен человек пытался заставить Луну служить себе. В Китае и других странах приливные воды с давних пор вращают мельничные жернова.

Отлив. Бухта Гертнера

В 1913 году в Северном море у Хузума была пущена в эксплуатацию первая «лунная» энергетическая станция. В Англии, Франции, США и особенно в Аргентине, ощущающей недостаток в горючем, создано много смелых проектов сооружения приливных станций. Однако дальше всех пошли советские инженеры, создавшие проект сооружения плотины длиною в 100 километров и высотою 15 метров в Мезенской губе Белого моря.

При приливе за плотиной образуется водохранилище емкостью в 2 тысячи квадратных километров. Две тысячи турбогенераторов дадут 36 миллиардов киловатт-часов. Такое количество энергии производили в 1929 году Франция, Италия и Швейцария, вместе взятые. Киловатт-час этой энергии будет стоить около одной копейки. К сожалению, «пульс» приливов и отливов моря бьется с неодинаковой силой, как и пульс человека. Приливы не дают постоянного, равномерного притока воды, и это затрудняет осуществление проекта.

Прилив бывает наиболее сильным тогда, когда Солнце и Луна притягивают массы воды в одном направлении. Приливы, при которых уровень воды поднимается до 20 метров, бывают при полной и молодой Луне. Они называются «сизигийными». В первой и последней четверти месяца, когда Луна находится под прямым углом к Солнцу, приливы бывают самыми низкими и называются «квадратурными».

Прилив и отлив моря имеют очень большое значение для мореплавания, и поэтому наступление их вычисляют заранее. Этот расчет так труден, что для составления ежегодного календаря приливов требуется много недель. Но изобретательный ум человека создал вычислительную машину, «электронный мозг» которой составляет прогнозы приливов за два дня. Календарь приливов показывает, что волны приливов проходят по всему земному шару через определенные промежутки времени. От морских берегов они поднимаются в реки.

libtime.ru

Приливы и отливы

Приливы

Уровень поверхности океанов и морей периодически, приблизительно два раза в течение суток, изменяется. Эти колебания называются приливами и отливами. Во время прилива уровень океана постепенно повышается и достигает наивысшего положения. При отливе уровень постепенно падает до наинизшего. При приливе вода течет к берегам, при отливе — от берегов.

Приливы и отливы — это стоячие волны. Они образуются вследствие влияния таких космических тел, как Луна и Солнце. По законам взаимодействия космических тел наша планета и Луна взаимно притягивают друг друга. Лунное притяжение столь велико, что поверхность океана как бы выгибается ему навстречу. Луна движется вокруг Земли, и за ней «бежит» по океану приливная волна. Дойдет волна до берега — вот и прилив. Пройдет немного времени, вода вслед за Луной отойдет от берега — вот и отлив. По тем же всеобщим космическим законам приливы и отливы образуются и от притяжения Солнца. Однако приливообразующая сила Солнца в связи с его удаленностью значительно меньше лунной, и если бы не было Луны, то приливы на Земле были бы в 2,17 раз меньше. Объяснение приливообразующих сил впервые было дано Ньютоном.

Приливы отличаются друг от друга продолжительностью и величиной. Чаще всего в течение суток происходит два прилива и два отлива. На островных дугах и побережьях Восточной Азии и Центральной Америки наблюдается один прилив и один отлив в течение суток.

Величина приливов еще более разнообразна, чем их период. Теоретически один лунный прилив равен 0,53 м, солнечный — 0,24 м. Таким образом, самый большой прилив должен иметь высоту 0,77 м. В открытом океане и у островов величина прилива довольно близка к теоретической: на Гавайских островах — 1 м, на острове Святой Елены — 1,1 м; на островах Фиджи — 1,7 м. У материков величина приливов колеблется от 1,5 до 2 м. Во внутренних морях приливы очень незначительны: в Черном — 13 см, в Балтийском — 4,8 см. Средиземное море считается бесприливным, но около Венеции приливы бывают до 1 м. Наиболее крупными можно отметить следующие приливы, зарегистрированные в Мировом океане:

В Атлантическом океане в заливе Фанди (США) прилив достиг высоты 16-17 м. Это самый большой показатель прилива на всем земном шаре.

На севере Охотского моря в Пенжинской губе высота прилива достигла 12-14 м. Это самый большой прилив у берегов России. Однако приведенные выше показатели приливов являются скорее исключением, чем правилом. В преобладающем большинстве пунктов измерений уровня приливов они невелики и редко превышают 2 м.

Значение приливов очень велико для морского судоходства, устройства портов. Каждая приливная волна несет огромный запас энергии.

geographyofrussia.com

Прилив и отлив — Википедия

Залив Фанди во время прилива и отлива.

Прили́в и отли́в — периодические вертикальные колебания уровня океана или моря, являющиеся результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями данного рельефа и проявляющиеся в периодическом горизонтальном смещении водных масс. Приливы и отливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.

Интенсивность этих явлений зависит от многих факторов, однако наиболее важным из них является степень связи водоёмов с мировым океаном. Чем более замкнут водоём, тем меньше степень проявления приливо-отливных явлений.

Так, например, на побережье Финского залива эти явления заметны только на мелководье, а периодически происходившие ранее наводнения в Петербурге объяснялись длинной волной, связанной с колебаниями атмосферного давления и нагонными западными ветрами.

С другой стороны, если в месте образования прилива достаточно большой амплитуды имеется сужающийся залив или устье реки, это может привести к образованию мощной приливной волны, которая поднимается вверх по течению реки, иногда на сотни километров. Из таких волн наиболее известны:

Лунный интервал приливов — это период времени с момента прохождения Луны через точку зенита над Вашей местностью до момента достижения наивысшего значения уровня воды во время прилива

Хотя для земного шара величина силы тяготения Солнца почти в 200 раз больше, чем силы тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не от величины гравитационного поля, а от степени его неоднородности. При увеличении расстояния от источника поля неоднородность уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то приливные силы, вызываемые солнечным притяжением, оказываются слабее.

Также одной из причин возникновения приливов и отливов является суточное (собственное) вращение Земли. Массы воды мирового океана, имеющие форму эллипсоида, большая ось которого не совпадает с осью вращения Земли, участвуют в её вращении вокруг этой оси. Это ведёт к тому, что в системе отсчёта, связанной с земной поверхностью, по океану бегут по взаимно противоположным сторонам земного шара две волны, приводящие в каждой точке океанского побережья к периодическим, два раза в сутки повторяющимся явлениям отлива, чередующихся с приливами.

Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:

суточное вращение земного шара;
деформация покрывающей земную поверхность водной оболочки, превращающая последнюю в эллипсоид.

Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.

При объяснении причин приливов внимание обычно обращается лишь на второй из этих факторов. Но расхожее объяснение рассматриваемого явления только действием приливных сил неполно.

Приливная волна, имеющая форму упомянутого выше эллипсоида, представляет собой суперпозицию двух «двугорбых» волн, образовавшихся в результате гравитационного взаимодействия планетной пары Земля — Луна и гравитационного взаимодействия этой пары с центральным светилом — Солнцем с одной стороны. Кроме того, фактором, определяющим образование этой волны, выступают силы инерции[1], имеющие место при обращении небесных тел вокруг общих для них центров масс.

Ежегодно повторяющийся приливно-отливной цикл остаётся неизменным вследствие точной компенсации сил притяжения между Солнцем и центром масс планетной пары и силами инерции, приложенными к этому центру.

Поскольку положение Луны и Солнца по отношению к Земле периодически меняется, меняется и интенсивность результирующих приливно-отливных явлений.

Отлив у Сен-Мало Отлив в заливе Мордвинова. Остров Сахалин. Сбор съедобного рачка «чилима».

Хосе де Акоста в своей Истории (1590), впервые объяснил природу отливов и приливов, периодичность и взаимосвязь с фазами Луны[2].

Отливы играли заметную роль в снабжении прибрежного населения морепродуктами, позволяя собирать на обнажившемся морском дне годную для еды пищу.

Малая вода (Бретань, Франция)

Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. В океане, где дно ровное, а суша далеко, полная вода проявляется как два «вздутия» водной поверхности: одно из них находится со стороны Луны, а другое — в противоположном конце земного шара. Также могут присутствовать ещё два меньших по размеру вздутия со стороны, направленной к Солнцу, и противоположной ему. Объяснение этому эффекту можно найти ниже, в разделе физика прилива.

Так как Луна и Солнце перемещаются относительно Земли, вместе с ними перемещаются и водные горбы, образуя прили́вные волны и прили́вные течения. В открытом море приливные течения имеют вращательный характер, а вблизи берегов и в узких заливах и проливах — возвратно-поступательный.

Если бы вся Земля была покрыта водой, мы бы наблюдали два регулярных прилива и отлива ежедневно. Но так как беспрепятственному распространению приливных волн мешают участки суши: острова и континенты, а также из-за действия силы Кориолиса на движущуюся воду, вместо двух приливных волн наблюдается множество маленьких волн, которые медленно (в большинстве случаев с периодом 12 ч 25,2 мин) обегают вокруг точки, называющейся амфидромической, в которой амплитуда прилива равна нулю. Доминирующая компонента прилива (лунный прилив М2) образует на поверхности Мирового океана около десятка амфидромических точек с движением волны по часовой стрелке и примерно столько же — против часовой (см. карту). Всё это делает невозможным предсказание времени прилива только на основе положений Луны и Солнца относительно Земли. Вместо этого используют «ежегодник приливов» — справочное пособие для вычисления времени наступления приливов и их высоты в различных пунктах земного шара. Также используются таблицы приливов, с данными о моментах и высотах малых и полных вод, вычисленными на год вперёд для основных прили́вных по́ртов.

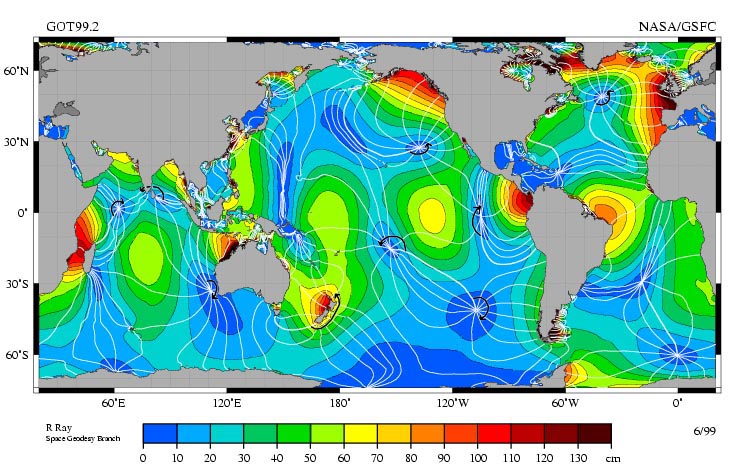Составляющая прилива M2

Если соединить на карте точки с одинаковыми фазами прилива, мы получим так называемые котидальные линии, радиально расходящиеся из амфидромической точки. Обычно котидальные линии характеризуют положение гребня приливной волны для каждого часа. Фактически котидальные линии отражают скорость распространения приливной волны за 1 час. Карты, на которых представлены линии равных амплитуд и фаз приливных волн, называются котидальными картами.

Высота прилива — разница между высшим уровнем воды при приливе (полная вода) и низшим её уровнем при отливе (малая вода). Высота прилива — величина непостоянная, однако средний её показатель приводится при характеристике каждого участка побережья.

В зависимости от взаимного расположения Луны и Солнца малая и большая приливные волны могут усиливать друг друга. Для таких приливов исторически сложились специальные названия:

Квадратурный прилив — наименьший прилив, когда приливообразующие силы Луны и Солнца действуют под прямым углом друг к другу (такое положение светил называется квадратурой).
Сизигийный прилив — наибольший прилив, когда приливообразующие силы Луны и Солнца действуют вдоль одного направления (такое положение светил называется сизигией).

Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.

Самые высокие приливы в мире[править]

Высочайшие на Земле приливы (15,6—18 м) наблюдаются в бухте Фанди, которая находится на восточном побережье Канады между Нью-Брансуиком и Новой Шотландией. Примерно такие же приливы и в заливе Унгава на севере Квебека.

На Европейском континенте самые высокие приливы (до 13,5 м) наблюдаются в Бретани у города Сен-Мало. Здесь приливная волна фокусируется береговой чертой полуостровов Корнуолл (Англия) и Котантен (Франция).

В России самые высокие приливы случаются в Пенжинской губе Охотского моря — до 12,9 м. Это точка самых высоких приливов на всём Тихом океане.

Физика прилива[править]

Современная формулировка[править]

Каждое из этих тел испытывает действие приливных сил, источником которых являются сила гравитации и внутренние силы, обеспечивающие целостность небесного тела, в роли которых выступает сила собственного притяжения, далее называемая самогравитацией. Наиболее наглядно возникновение приливных сил прослеживается на примере системы Земля — Солнце.

Приливная сила представляет собой результат конкурирующего взаимодействия силы тяготения, направленной к центру гравитации и убывающей обратно пропорционально квадрату расстояния от него, и фиктивной центробежной силы инерции, обусловленной обращением небесного тела вокруг этого центра. Эти силы, будучи противоположными по направлению, совпадают по величине только в центре масс каждого из небесных тел. Благодаря действию внутренних сил Земля обращается вокруг центра Солнца как целое с постоянной угловой скоростью для каждого элемента составляющей её массы. Поэтому по мере удаления этого элемента массы от центра гравитации действующая на него центробежная сила растёт пропорционально квадрату расстояния.

Более детальное распределение приливных сил в их проекции на плоскость, перпендикулярную плоскости эклиптики, приведены на рис. 1.

Рис. 1. Схема распределения приливных сил в проекции на плоскость, перпендикулярную эклиптике. Тяготеющее тело либо справа, либо слева

Достигаемое в результате действия приливных сил воспроизводство изменений формы подвергаемого их действию тел может, в соответствии с ньютонианской парадигмой, быть достигнуто лишь в том случае, если эти силы полностью скомпенсированы иными силами, в число которых может входить и сила всемирного тяготения.

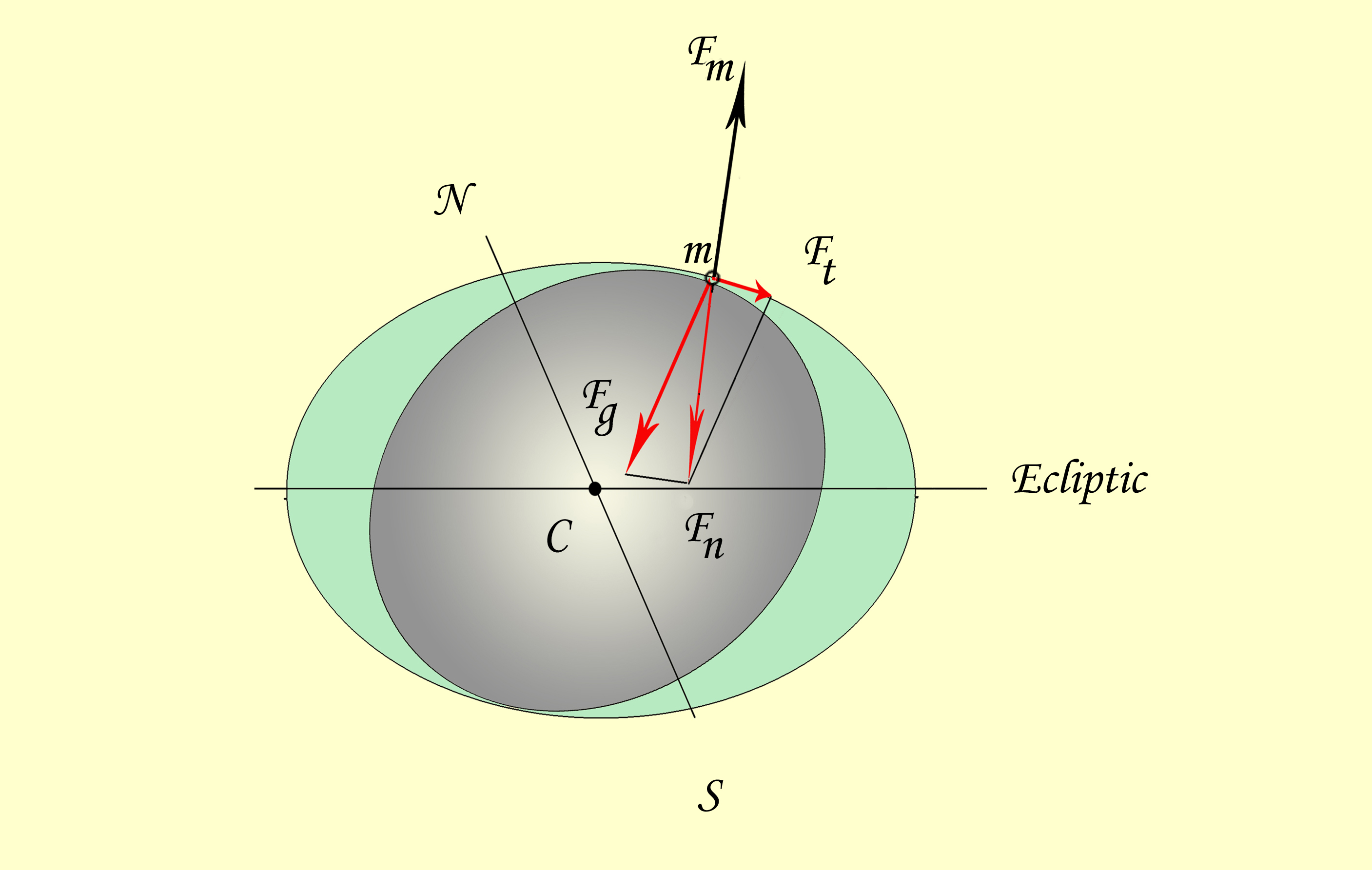Рис. 2. Деформация водной оболочки Земли как следствие баланса приливной силы, силы самогравитации и силы реакции воды на усилие сжатия

В результате сложения этих сил и возникают симметрично по обе стороны земного шара приливные силы, направленные в разные стороны от него. Приливная сила, направленная к Солнцу, имеет гравитационную природу, а направленная от Солнца есть следствие фиктивной силы инерции.

Эти силы крайне слабы и не идут ни в какое сравнение с силами самогравитации (создаваемое ими ускорение в 10 миллионов раз меньше ускорения свободного падения[3]). Однако они вызывают сдвиг частиц воды Мирового океана (сопротивление сдвигу в воде при малых скоростях движения практически равно нулю, в то время как сжатию — чрезвычайно велико), до тех пор, пока касательная к поверхности воды не станет перпендикулярной результирующей силе.

В итоге на поверхности Мирового океана возникает волна, занимающая постоянное положение в системах взаимно тяготеющих тел, но бегущая по поверхности океана совместно с суточным движением его дна и берегов. Таким образом (в пренебрежении океаническими течениями) каждая частица воды дважды совершает в течение суток колебательное движение вверх-вниз.

Горизонтальное движение воды наблюдается лишь у берегов как следствие подъёма её уровня. Скорость движения тем больше, чем более полого расположено морское дно.

Приливообразующий потенциал[править]

(концепция акад. Шулейкина[4])

Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть $\mathbf{r}'$ — радиус-вектор, направленный от пробного тела в сторону Луны, $r'$ — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна

$\mathbf{F}=\frac{G{{M}_{L}}}{r{{'}^{3}}}\mathbf{r}'$ (1)

где $G{{M}_{L}}$ — селенометрическая гравитационная постоянная. Пробное тело поместим в точку $P$ . Сила притяжения пробного тела, помещённого в центр масс Земли будет равна

${{\mathbf{F}}_{0}}=\frac{G{{M}_{L}}}{{{r}^{3}}}\mathbf{r}$ (2)

Здесь под $\mathbf{r}$ и $r$ понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения

${{\mathbf{F}}_{fl}}=\mathbf{F}-{{\mathbf{F}}_{0}}$ (3)

В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна ${}^{G{{M}_{L}}}\!\!\diagup\!\!{}_{r'}\;$ Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось $Ox$ проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы ${{\mathbf{F}}_{0}}$ будет равна $\frac{G{{M}_{L}}}{{{r}^{2}}}x+\operatorname{const}$ . Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его $\delta W$ , получим $\delta W=\frac{G{{M}_{L}}}{r'}-\frac{G{{M}_{L}}}{{{r}^{2}}}x-\operatorname{const}$ Постоянную $\operatorname{const}$ определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли $x=0$ , $r'=r$ Отсюда следует, что $\frac{G{{M}_{L}}}{r}=\operatorname{const}$ . Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде

$\frac{G{{M}_{L}}}{r'}-\frac{G{{M}_{L}}}{{{r}^{2}}}x-\frac{G{{M}_{L}}}{r}$ (4)

Поскольку

$r'=\sqrt{{{\left( r-x \right)}^{2}}+{{y}^{2}}+{{z}^{2}}}$

то

$\frac{1}{r'}=\frac{1}{r}{{\left[ {{\left( 1-\frac{x}{r} \right)}^{2}}+\frac{{{y}^{2}}+{{z}^{2}}}{{{r}^{2}}} \right]}^{-\frac{1}{2}}}$

При малых величинах ${x}/{r}\;$ , ${y}/{r}\;$ , ${z}/{r}\;$ , учитывая второй порядок малости, последнее выражение можно представить в следующем виде

$\frac{1}{r'}\approx \frac{1}{r}\left( 1+\frac{x}{r}+\frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)$ (5)

Подставив (5) в (4), получим

$\delta W=G{{M}_{L}}\frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}$ (6)

Деформация поверхности планеты под действием приливов и отливов[править]

Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен $\frac{GM}{R}$ . Для точки $P$ . , находящейся на расстоянии $\rho$ от центра сферы, гравитационный потенциал Земли равен $\frac{GM}{\rho }$ . Сократив на гравитационную постоянную, получим $\frac{1}{\rho }+\frac{{{M}_{L}}}{M}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}=\frac{1}{R}$ . Здесь переменными величинами являются $x,y,z$ и $\rho$ . Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой $\mu$ и решим полученное выражение относительно $\rho$ :

$\rho =R{{\left( 1-\mu \frac{R}{r}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)}^{-1}}\approx R\left( 1+\mu \frac{R}{r}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)$

Так как ${{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}$ с той же степенью точности получим

$\frac{{{x}^{2}}}{{{R}^{2}}}\left( 1-2\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)+\frac{{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}}\left( 1+\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)=1$

Учитывая малость отношения ${R}/{r}\;$ последние выражения можно записать так

$\frac{{{x}^{2}}}{{{R}^{2}}\left( 1+2\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)}+\frac{{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left( 1-\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)}=1$

Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью $Ox$ , т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны

$a=\left( 1+\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)R,\,\,\,b=c=\left( 1-\mu \frac{{{R}^{3}}}{2{{r}^{3}}} \right)R$

Приведём в конце небольшую численную иллюстрацию данного эффекта. Вычислим приливные «горбы» на Земле, вызванные притяжением Луны и Солнца.

Радиус Земли равен $R=6378$ км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты $r=384,4\cdot {{10}^{3}}$ км, отношение массы Земли к массе Луны равно 81:1 ( $\mu=0,012345679$ ). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.

Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное $r=149,6\cdot {{10}^{6}}$ км, и отношение массы Солнца к массе Земли $\mu=332 982$ . В этом случае получаем величину «горба» около 16 см.

Приливы и отливы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. — М.: ГИТТЛ, 1957
Шулейкин В. В. Физика моря. — М.: Изд-во «Наука», Отделение наук о Земле АН СССР, 1967
Войт С. С. Что такое приливы. Редколлегия научно-популярной литературы АН СССР.
Дуванин А. И. Приливы в море. — Л.: ГИМИЗ, 1960
Белонучкин В. Приливные силы // Квант. — М., 1989. —.

wp.wiki-wiki.ru

Прилив и отлив — WiKi

Залив Фанди во время прилива и отлива.

Лунный интервал приливов — это период времени с момента прохождения Луны через точку зенита над вашей местностью до момента достижения наивысшего значения уровня воды во время прилива.

Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:

суточное вращение земного шара;
деформация покрывающей земную поверхность водной оболочки, превращающая последнюю в эллипсоид.

Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.

Отлив у Сен-Мало

История изучения и использования приливов

Отлив в заливе Мордвинова. Остров Сахалин. Сбор съедобного рачка «чилима».

Гай Юлий Цезарь в книге "Записки о Галльской войне" (книга 4 гл. 29) связывает необычно высокий прилив у берегов Британии с наступившим новолунием, сообщая что до этого момента связь новолуния с высотой прилива римлянам не была известна.

Хосе де Акоста в своей Истории (1590) собрал доказательства связи отливов и приливов с фазами Луны: он указал, что период приливов, происходящих дважды в сутки, отличается на три четверти часа от солнечных суток, что известна также месячная периодичность приливов, а также добавил новое доказательство: приливы на обоих берегах Панамского перешейка происходят практически одновременно. Хосе де Акоста назвал приливы "одной из замечательных тайн Природы".[2].

Немецкий астроном Иоганн Кеплер, пришедший на основании своих наблюдений над планетами к идее всемирного тяготения, выдвинул гипотезу о том, что именно гравитация Луны является причиной приливов:

Когда Луна находится непосредственно над Атлантическим, так называемым Южным, Восточным или Индийским океаном, то она притягивает воды, омывающие земной шар. Не встречая на своем пути континентов, воды со всех сторон устремляются к обширному участку, находящемуся прямо под Луной, а берега при этом обнажаются. Но пока воды находятся в движении, Луна успевает переместиться и не располагается более прямо над океаном, в силу чего масса воды, бьющая в западный берег, перестает испытывать действие лунного притяжения и обрушивается на восточный берег. [3].

Не зная точного закона всемирного тяготения, Кеплер не смог создать количественную теорию приливов.

Терминология

Малая вода (Бретань, Франция)

Составляющая прилива M2

Квадратурный прилив — наименьший прилив, когда приливообразующие силы Луны и Солнца действуют под прямым углом друг к другу (такое положение светил называется квадратурой).
Сизигийный прилив — наибольший прилив, когда приливообразующие силы Луны и Солнца действуют вдоль одного направления (такое положение светил называется сизигией).

Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.

Самые высокие приливы в мире

Физика прилива

Современная формулировка

Малая вода. Гавань деревни Юйао на Восточно-Китайском море. (Уезд Цаннань, Чжэцзян)

Применительно к планете Земля приливной эффект является причиной смещения гравитационного поля Земли в сторону массы Луны.

Приливообразующий потенциал

(концепция акад. Шулейкина[4])

Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть r′{\displaystyle \mathbf {r} '} — радиус-вектор, направленный от пробного тела в сторону Луны, r′{\displaystyle r'} — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна

F=GMLr′3r′{\displaystyle \mathbf {F} ={\frac {G{{M}_{L}}}{r{{'}^{3}}}}\mathbf {r} '} (1)

где GML{\displaystyle G{{M}_{L}}} — селенометрическая гравитационная постоянная. Пробное тело поместим в точку P{\displaystyle P} . Сила притяжения пробного тела, помещённого в центр масс Земли будет равна

F0=GMLr3r{\displaystyle {{\mathbf {F} }_{0}}={\frac {G{{M}_{L}}}{{r}^{3}}}\mathbf {r} } (2)

Здесь под r{\displaystyle \mathbf {r} } и r{\displaystyle r} понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения

Ffl=F−F0{\displaystyle {{\mathbf {F} }_{fl}}=\mathbf {F} -{{\mathbf {F} }_{0}}} (3)

В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна GML╱r′{\displaystyle {}^{G{{M}_{L}}}\!\!\diagup \!\!{}_{r'}\;} Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось Ox{\displaystyle Ox} проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы F0{\displaystyle {{\mathbf {F} }_{0}}} будет равна GMLr2x+const{\displaystyle {\frac {G{{M}_{L}}}{{r}^{2}}}x+\operatorname {const} } . Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW{\displaystyle \delta W} , получим δW=GMLr′−GMLr2x−const{\displaystyle \delta W={\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-\operatorname {const} } Постоянную const{\displaystyle \operatorname {const} } определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли x=0{\displaystyle x=0} , r′=r{\displaystyle r'=r} Отсюда следует, что GMLr=const{\displaystyle {\frac {G{{M}_{L}}}{r}}=\operatorname {const} } . Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде

GMLr′−GMLr2x−GMLr{\displaystyle {\frac {G{{M}_{L}}}{r'}}-{\frac {G{{M}_{L}}}{{r}^{2}}}x-{\frac {G{{M}_{L}}}{r}}} (4)

Поскольку

r′=(r−x)2+y2+z2{\displaystyle r'={\sqrt {{{\left(r-x\right)}^{2}}+{{y}^{2}}+{{z}^{2}}}}}

то

1r′=1r[(1−xr)2+y2+z2r2]−12{\displaystyle {\frac {1}{r'}}={\frac {1}{r}}{{\left[{{\left(1-{\frac {x}{r}}\right)}^{2}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{r}^{2}}}\right]}^{-{\frac {1}{2}}}}}

При малых величинах x/r{\displaystyle {x}/{r}\;} , y/r{\displaystyle {y}/{r}\;} , z/r{\displaystyle {z}/{r}\;} , учитывая второй порядок малости, последнее выражение можно представить в следующем виде

1r′≈1r(1+xr+2x2−y2−z22r2){\displaystyle {\frac {1}{r'}}\approx {\frac {1}{r}}\left(1+{\frac {x}{r}}+{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)} (5)

Подставив (5) в (4), получим

δW=GML2x2−y2−z22r3{\displaystyle \delta W=G{{M}_{L}}{\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}} (6)

Деформация поверхности планеты под действием приливов и отливов

Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен GMR{\displaystyle {\frac {GM}{R}}} . Для точки P{\displaystyle P} . , находящейся на расстоянии ρ{\displaystyle \rho } от центра сферы, гравитационный потенциал Земли равен GMρ{\displaystyle {\frac {GM}{\rho }}} . Сократив на гравитационную постоянную, получим 1ρ+MLM⋅2x2−y2−z22r3=1R{\displaystyle {\frac {1}{\rho }}+{\frac {{M}_{L}}{M}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}}={\frac {1}{R}}} . Здесь переменными величинами являются x,y,z{\displaystyle x,y,z} и ρ{\displaystyle \rho } . Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой μ{\displaystyle \mu } и решим полученное выражение относительно ρ{\displaystyle \rho } :

ρ=R(1−μRr⋅2x2−y2−z22r2)−1≈R(1+μRr⋅2x2−y2−z22r2){\displaystyle \rho =R{{\left(1-\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}^{-1}}\approx R\left(1+\mu {\frac {R}{r}}\cdot {\frac {2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}}}\right)}

Так как ρ2=x2+y2+z2{\displaystyle {{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}} с той же степенью точности получим

x2R2(1−2μR3r3)+y2+z2R2(1+μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{R}^{2}}}\left(1-2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)+{\frac {{{y}^{2}}+{{z}^{2}}}{{R}^{2}}}\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)=1}

Учитывая малость отношения R/r{\displaystyle {R}/{r}\;} последние выражения можно записать так

x2R2(1+2μR3r3)+y2+z2R2(1−μR3r3)=1{\displaystyle {\frac {{x}^{2}}{{{R}^{2}}\left(1+2\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}+{\frac {{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left(1-\mu {\frac {{R}^{3}}{{r}^{3}}}\right)}}=1}

Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью Ox{\displaystyle Ox} , т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны

a=(1+μR3r3)R,b=c=(1−μR32r3)R{\displaystyle a=\left(1+\mu {\frac {{R}^{3}}{{r}^{3}}}\right)R,\,\,\,b=c=\left(1-\mu {\frac {{R}^{3}}{2{{r}^{3}}}}\right)R}

Радиус Земли равен R=6378{\displaystyle R=6378} км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты r=384,4⋅103{\displaystyle r=384,4\cdot {{10}^{3}}} км, отношение массы Земли к массе Луны равно 81:1 (μ=0,012345679{\displaystyle \mu =0,012345679} ). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.

Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное r=149,6⋅106{\displaystyle r=149,6\cdot {{10}^{6}}} км, и отношение массы Солнца к массе Земли μ=332982{\displaystyle \mu =332982} . В этом случае получаем величину «горба» около 16 см.

См. также

Примечания

Литература

Приливы и отливы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. — М.: ГИТТЛ, 1957
Шулейкин В. В. Физика моря. — М.: Изд-во «Наука», Отделение наук о Земле АН СССР, 1967
Войт С. С. Что такое приливы. Редколлегия научно-популярной литературы АН СССР.
Дуванин А. И. Приливы в море. — Л.: ГИМИЗ, 1960
Белонучкин В. Приливные силы // Квант. — М., 1989. — № 12.

Ссылки

ru-wiki.org

Прилив и отлив Википедия

Залив Фанди во время прилива и отлива.

Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:

суточное вращение земного шара;
деформация покрывающей земную поверхность водной оболочки, превращающая последнюю в эллипсоид.

Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.

Отлив у Сен-Мало

ru-wiki.ru

Отливы и приливы на Бали. Как читать график приливов.

Статья последний раз обновлялась в январе 2018 года.

Информация про приливы и отливы на Бали будет полезна как начинающим серферам, так и всем тем, кто приезжает ради пляжного отдыха и хочет разобраться с тем, куда девается вода в океане и почему становится так мелко, что купаться невозможно. А заодно развеете себя по поводу частых туристических мифов а-ля “а правда ли что утром обычно прилив” или “а правда что в Нуса Дуа нет приливов?”

Если почитать какие-нибудь туристические форумы, то можно найти много легенд про отливы, поэтому здесь я простым и понятным любому человеку языком, расскажу все самое главное, что нужно знать. Причем это информация пригодится вам не только по Бали, но и когда вы поедете в другую страну, расположенную на берегу океана.

Так же я расскажу, как пользоваться графиком приливов и отливов: делать это совсем не сложно, и вы сможете сами прогнозировать, когда ждать мелкую воду, а когда глубина будет хорошей.

Люди, которые не сталкивалось ранее с океанским побережьем и приливами-отливами и которые ждут от Бали идеального пляжного отдыха, в итоге остаются разочарованы тем, что “половину отпуска вообще в океане не было”.

Приливы и отливы касаются всех пляжей Бали, но в Сануре, на Буките, в Нуса Дуа – они заметнее всего. В том же Сануре в дни сильных отливов пляж оголяется на многие сотни метров и чтобы искупаться, вначале надо долго идти, а потом все равно плескаться на мелководье. В Нуса Дуа ситуация визуально обстоит лучше, но по факту, если уж пришел отлив, то он пришел на весь Бали (а не на конкретный пляж). На Буките много красивых диких пляжей, которые во время приливов вообще становятся не купабельны: полностью оголяется риф и купаться становится негде.

Два самых главных вопроса от туристов и мифа, которые я хочу сразу опровергнуть:

#1 – “Я слышал, что есть какие-то пляжи Бали, где нет отлива”. Это не так, как я уже писала выше, отливы-приливы приходят на все пляжи Бали в одно и то же время. Но если пляжи, где глубина дна такая, что отлив не так ярко выражен. (Например, на пляжах Дримленд или Бату Болонг даже во времена сильнейших отливов не оголяется дно)

#2 – “Друзья были в прошлом году и говорят, что с утра нормально купаться, потому что утром как рах прилив.” Время приливов и отливов не одинаковое каждый день и сдвигается каждый день на часа. То, что было год назад никак не отражает ситуацию сегодня. Надо смотреть прогноз приливов на конкретную неделю. Как это делать я расскажу ниже.

пляж Гринбол на отливе

Немного занудной информации. Приливы-отливы – это изменение в уровне воды у берега. При сильном отливе береговая линия сильно оголяется, вода “уходит” и до глубокой воды нужно долго топать по мелководью. При сильном приливе береговая линия наоборот сокращается и пляж почти “исчезает”.

Приливы-отливы появляются на тех океанических и некоторых морских побережьях, где территория водоема не замкнута сушей и соединяется с мировым океаном. На Бали Индийский океан (на южном побережье) и поэтому приливы-отливы заметны сильно.

Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. То, что посередине мы серферы обычно называем “средней водой”.

На появление приливов влияет притяжение луны и солнца, точнее совокупность этих притяжений. Причем луна влияет сильнее, поэтому приливы-отливы сильно зависят от фазы луны. То есть на то, прилив сейчас или отлив в конкретной точке земного шара, влияет то, где сейчас находится луна относительно этой точки.

Посмотрите на картинку выше. Луна как будто бы “тянет” к себе воду и на поверхности земли образуется водяной холм (отмечено голубым на картинке), он и выражается в приливе в этой точке земли (и той что “под нею” – противоположной стороне глобуса). Но луна не стоит на месте, она постоянно двигается и таким образом прилив “двигается” по земле: куда пришла луна, туда пришел прилив, а откуда она ушла – там становится отлив. То есть это то, как определяется на графике приливов, во сколько ждать малой воды, а во сколько полной.

Но это еще не вся история. Помимо того, что меняется время, также меня и степень изменения уровня воды (“высота прилива”). В какие-то недели разница между полной и малой воды еле заметна, а в какие-то она просто огромная и кажется, что действительно “весь океан ушел”.

И вот откуда это берется. Помимо луны, которая вращается вокруг земли, есть еще такие факторы, как земля, которая вращается вокруг своей оси, и солнце вокруг вращаются вместе земля с луной. Обилие этих вращений так влияет на ситуацию с отливами и приливами, что в какие-то период (такие как полнолуние и новолуние) уровень воды в течение дня будет сменяться очень значительно, а вот когда “средняя луна” (официальное название “квадратурный прилив, это 1 и 3 фаза луны, то есть все что между приливом и отливом).

В английском используются следующие термины: high tide – высокая вода, low tide – низкая вода, fullmoon – полнолуние, newmoon – новолуние.

В общем, если вы сейчас только сильнее запутались, не пытайтесь понять эту информацию на уровне физики и географии, а просто переходите к следующей главе, где будет главное: как узнать когда отлив, а когда прилив, и как часто это происходит на Бали.

Как часто случаются приливы и отливы?

Как и в большинстве мест, на Бали, за каждые сутки происходит по два прилива и два отлива. Смена воды происходит примерно каждые 6 часов. Что это означает? Если в данный момент на часах 7 утра и прилив, то где-то через часов шесть будет отлив, а потом еще через шесть – снова прилив.

Что важно, так это то, что вода не стоит на месте и постоянно то приливает, то отливает. Если бы уровень воды можно было бы изобразить на графике (см. картинку ниже), то выглядело бы это примерно так. То есть за час можно уже поменяться уровень воды: он либо немного вырастет, либо немного упадет. За шесть часов, о которых я говорила выше, уровень воды поменяется кардинально.

Еще одна важная информация про приливы-отливы, время, когда будет максимальная вода, а когда минимальная, сдвигается каждые сутки примерно на час. (Все это не точно на час, но для удобства использования проще мыслить “сдвигается на час”). То есть если сегодня максимально большая вода будет в 7:00 утра и в 19:00, то завтра в 8 утра и в 20:00.

Пример: мы сегодня в 7 утра наблюдаем пик прилива. Что нам это дает? Во-первых, мы знаем, что надо быстрее бежать купаться, так как через несколько часов вода начнет уходить. Во-вторых, мы знаем, что ближе к закату (в 19:00) тоже будет прилив, а значит мы сможем снова покупаться. Ну и в-третьих, мы можем рассчитать, что завтра с утра тоже будет достаточно воды, правда теперь пик прилива сдвинется к 8 утра, послезавтра к 9, а через неделю приливы уже будут в обеденное время.

На картинке ниже один из пляжей Нуса Дуа на сильном отливе. Во время прилива этот пляж полностью скрыт водой и спуститься к нему невозможно.

Помимо того, что меняется время, приливов и отливов, также меняется их степень. Как я рассказывала выше, на это влияет положение луны. Во время новолуния и полнолуния (а они происходят два раза в месяц), разница самой высокой водой и самой низкой на Бали просто чудовищна. То есть именно в эти дни ждите того, что воды будет то очень много и она может скрыть большую часть пляжа, то ее будет совсем мало и дно океана может оголиться на сотни метров и где-то коралловый риф полностью покажется из воды.

(Кстати, если вы когда-нибудь были на севере Франции в Нормандии, там есть такой город-остров Мон-Сен-Мишель, во время отлива к нему можно дойти по пляжу пешком (около полкилометра!), а во время прилива, он полностью окружен)

Эти дни я люблю, так как подгадав отлив, можно по многим пляжам Букита гулять далеко, так как пляжи открываются и появляется возможность дойти от одного до другого. Так можно в сильный отлив дойти от Дримленда до Бингина, или от Меласти до Гринбола и так далее.

В другие дни, когда и до полнолуния/новолуния далеко (около недели) уровень воды почти не меняется и в целом воды, что называется “ни много ни мало”, так как она почти весь день держится на среднем уровне, не поднимаясь высоко и не падая низко.

Для наглядности посмотрите на график ниже (и нет, не надо пугаться), видите как синее – уровень воды – то сильно меняется (в левой части графика), то не так сильно – в правой части графика. Все потому, что дни в левой части графика они сразу после новолуния, а вот ближе к правой – как раз эта самая “средняя луна” или в данном случае первая фаза луны.

Есть специальная таблица, которая выпускается на каждый месяц каждого года, по которой серферы (а также рыбаки и лодочники) узнают, когда им ждать прилива, а когда отлива.

По-русски мы называем эту таблицу “график приливов”, а по-анлийски “тайдчарт” (tide chart).

Эти таблицы готовятся для портов, чтобы корабли знали, когда воды достаточно, чтобы не сесть на мель. У каждого порта такая таблица своя, то есть если вы не на Бали, а где-то еще, то вам надо искать таблицу ближайшего порта к вашему пляжу.

По Бали (по южной его части) традиционно используется таблица порта Беноа, который находится в Нуса Дуа. Этой таблицей пользуются все, кто живет на Бали, независимо от того, живут они в Нуча Дуа, Чангу или в Сануре.

Где взять такую таблицу? По поиску “график приливов-отливов бали” (или bali tide chart) вы обычно можете найти сайты, публикующие такие таблицы. Дальше вам нужно найти правильный год и месяц.

На BaliBlogger актуальные тайдчарты на весь год висят тут:

http://baliblogger.ru/forecast

Разобраться в графике очень легко. В таблице вы находите нужный день (чаще всего это строки), а в столбцах выбираете нужное время дня. На пересечении выходит значение уровня воды на данный момент – в метрах.

Что означают эти цифры применительно к Бали:

– значение около 1,5 означает “среднюю воду”, то есть когда воды и не много и не мало, а как раз самое то.– полный прилив – это 1.8-2.2– отлив – все что меньше 1,2– максимально сильные приливы на Бали (в полнолуние и новолуние) могут доходить до 2.6– максимально сильные отливы (опять же в полнолуние и новолуние) могут достигать 0 метров и даже -0.1

Для купания и для серфинга (если вы не про) на большинстве пляжей надо ориентироваться на воду больше 1.5, а все что будет меньше 1.0, скорее всего уже будет оголяться риф (где он есть) или будет мелко.

На картинке выше график приливов и отливов за конец декабря 2017 и начало января 2018. Красным подчеркнуты часы, когда ждать меньше всего воды, эти часы не очень подходят для купания, лучше выбирать другое время.

Если вы серфер, но не понимаете как читать тайдчарт и как приливы-отливы влияют на серфинг, то вам однозначно надо отправляться школу или к инструктору, и ни в коем случае не кататься самостоятельно, пока вы в этом вопросе не разберетесь. На большинстве рифовых спотов Бали кататься в отлив – если вы не про – чревато последствиями. Плюс в принципе, каждый серфспот лучше работает на определенной воде, если вы приехали в неудачное время, то и волны могут вам достаться плохие: слишком резкие, слишком жирные, закрывашки итп.

У каждого серфспота есть свой определенный промежуток между отливом и приливом, когда там следует серфить. В целом этот промежуток так же зависит и от вашего опыта. Общее правило такое – если вы начинающий серфер, то лучше не ходить на рифовый спот на отливе.

Катание на серфе на рифовых спотах в отлив может закончится серьезной травмой, если вы не обладаете опытом: волной вас может прижать ко дну и раскатать об острый риф. В лучшем случае вы отделаетесь порезами и ссадинами. Непродвинутым серферам БалиБлоггер вообще не рекомендует выходить на рифовые споты при значения прилива менее 1.8; все серфспоты разные, но на большинство рифовых спотах Бали при значении ниже этого вы будете доставать до дна ногами, а значит упасть с волны будет опасно. Кроме того, чем сильнее отлив, тем резче и сложнее волна.

На бичбрейке вроде пляжа Куты тоже невозможно серфить на отливе (значения ниже 1 метра), так как волны будут просто захлопываться и на них невозможно кататься. Для бичбрейка в Куте лучше всего подходит все, что выше 1.5, идеально 1.8.

Серфпрогноз по Бали и тайдчарт Полезная статья про безопасность в океане

www.baliblogger.ru

Прилив и отлив — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Таким образом, ключевыми моментами в объяснении приливно-отливных явлений являются:

суточное вращение земного шара;
деформация покрывающей земную поверхность водной оболочки, превращающая последнюю в эллипсоид.

Отсутствие одного из этих факторов исключает возможность появления приливов и отливов.

История изучения и использования приливов

Терминология

Квадратурный прилив — наименьший прилив, когда приливообразующие силы Луны и Солнца действуют под прямым углом друг к другу (такое положение светил называется квадратурой).
Сизигийный прилив — наибольший прилив, когда приливообразующие силы Луны и Солнца действуют вдоль одного направления (такое положение светил называется сизигией).

Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.

Самые высокие приливы в мире

Физика прилива

Современная формулировка

Применительно к планете Земля причиной приливов является нахождение планеты в гравитационном поле, создаваемом Солнцем и Луной. Поскольку создаваемые ими эффекты независимы, то воздействие этих небесных тел на Землю можно рассматривать по отдельности. В таком случае для каждой пары тел можно считать, что каждое из них обращается вокруг общего центра гравитации. Для пары Земля — Солнце этот центр находится в глубине Солнца на расстоянии 451 км от его центра. Для пары Земля — Луна он находится в глубине Земли на расстоянии 2⁄3 её радиуса от центра. И именно это движение Земли (её центра) вокруг общего центра масс системы Земля-Луна является непосредственной причиной появления двух приливных горбов: в соответствии с третьим законом Кеплера, материальная точка, находящаяся ближе к центру масс, должна двигаться быстрее, чем точка, находящаяся дальше. Таким образом, точка (в нашем случае - точка Земли), расположенная ближе к центру масс, будет стремиться опередить в этом движении все остальные точки, а ей противоположная - отстать.

Эти силы крайне слабы и не идут ни в какое сравнение с силами самогравитации (создаваемое ими ускорение в 10 миллионов раз меньше ускорения свободного падения[1]). Однако они вызывают сдвиг частиц воды Мирового океана (сопротивление сдвигу в воде при малых скоростях движения практически равно нулю, в то время как сжатию — чрезвычайно велико), до тех пор, пока касательная к поверхности воды не станет перпендикулярной результирующей силе.

Горизонтальное движение воды наблюдается лишь у берегов как следствие подъёма её уровня. Скорость движения тем больше, чем более полого расположено морское дно..

Приливообразующий потенциал

(концепция акад. Шулейкина[3])

Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть <math>\mathbf{r}'</math> — радиус-вектор, направленный от пробного тела в сторону Луны, <math>r'</math> — длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна

<math>\mathbf{F}=\frac{G{{M}_{L}}}{r{{'}^{3}}}\mathbf{r}'</math> (1)

где <math>G{{M}_{L}}</math> — селенометрическая гравитационная постоянная. Пробное тело поместим в точку <math>P</math>. Сила притяжения пробного тела, помещённого в центр масс Земли будет равна

<math>{{\mathbf{F}}_{0}}=\frac{G{{M}_{L}}}{{{r}^{3}}}\mathbf{r}</math> (2)

Здесь под <math>\mathbf{r}</math> и <math>r</math> понимаются радиус-вектор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения

<math>{{\mathbf{F}}_{fl}}=\mathbf{F}-{{\mathbf{F}}_{0}}</math> (3)

В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна <math>{}^{G{{M}_{L}}}\!\!\diagup\!\!{}_{r'}\;</math> Вторая сила приложена к центру масс Земли и является строго постоянной величиной. Для получения силовой функции для этой силы мы введём временную систему координат. Ось <math>Ox</math> проведём из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы <math>{{\mathbf{F}}_{0}}</math> будет равна <math>\frac{G{{M}_{L}}}{{{r}^{2}}}x+\operatorname{const}</math>. Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его <math>\delta W</math>, получим <math>\delta W=\frac{G{{M}_{L}}}{r'}-\frac{G{{M}_{L}}}{{{r}^{2}}}x-\operatorname{const}</math> Постоянную <math>\operatorname{const}</math> определим из условия нормировки, согласно которому приливообразующий потенциал в центре Земли равен нулю. В центре Земли <math>x=0</math>, <math>r'=r</math> Отсюда следует, что <math>\frac{G{{M}_{L}}}{r}=\operatorname{const}</math>. Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде

<math>\frac{G{{M}_{L}}}{r'}-\frac{G{{M}_{L}}}{{{r}^{2}}}x-\frac{G{{M}_{L}}}{r}</math> (4)

Поскольку

<math>r'=\sqrt{{{\left( r-x \right)}^{2}}+{{y}^{2}}+{{z}^{2}}}</math>

то

<math>\frac{1}{r'}=\frac{1}{r}{{\left[ {{\left( 1-\frac{x}{r} \right)}^{2}}+\frac{{{y}^{2}}+{{z}^{2}}}{{{r}^{2}}} \right]}^{-\frac{1}{2}}}</math>

При малых величинах <math>{x}/{r}\;</math>, <math>{y}/{r}\;</math>, <math>{z}/{r}\;</math>, учитывая второй порядок малости, последнее выражение можно представить в следующем виде

<math>\frac{1}{r'}\approx \frac{1}{r}\left( 1+\frac{x}{r}+\frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)</math> (5)

Подставив (5) в (4), получим

<math>\delta W=G{{M}_{L}}\frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}</math> (6)

Деформация поверхности планеты под действием приливов и отливов

Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущённый гравитационный потенциал Земли на поверхности будет равен <math>\frac{GM}{R}</math>. Для точки <math>P</math>. , находящейся на расстоянии <math>\rho </math> от центра сферы, гравитационный потенциал Земли равен <math>\frac{GM}{\rho }</math>. Сократив на гравитационную постоянную, получим <math>\frac{1}{\rho }+\frac{{{M}_{L}}}{M}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{3}}}=\frac{1}{R}</math>. Здесь переменными величинами являются <math>x,y,z</math> и <math>\rho </math>. Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой <math>\mu </math> и решим полученное выражение относительно <math>\rho </math>:

<math>\rho =R{{\left( 1-\mu \frac{R}{r}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)}^{-1}}\approx R\left( 1+\mu \frac{R}{r}\cdot \frac{2{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{r}^{2}}} \right)</math>

Так как <math>{{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}</math> с той же степенью точности получим

<math>\frac{{{x}^{2}}}{{{R}^{2}}}\left( 1-2\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)+\frac{{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}}\left( 1+\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)=1</math>

Учитывая малость отношения <math>{R}/{r}\;</math> последние выражения можно записать так

<math>\frac{{{x}^{2}}}{{{R}^{2}}\left( 1+2\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)}+\frac{{{y}^{2}}+{{z}^{2}}}{{{R}^{2}}\left( 1-\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)}=1</math>

Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью <math>Ox</math>, т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида в первом приближении равны

<math>a=\left( 1+\mu \frac{{{R}^{3}}}{{{r}^{3}}} \right)R,\,\,\,b=c=\left( 1-\mu \frac{{{R}^{3}}}{2{{r}^{3}}} \right)R</math>

Радиус Земли равен <math>R=6378</math> км, расстояние между центрами Земли и Луны с учётом нестабильности лунной орбиты <math>r=384,4\cdot {{10}^{3}}</math> км, отношение массы Земли к массе Луны равно 81:1 (<math>\mu=0,012345679</math>). Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.

Для вычисления приливного «горба», вызванного Солнцем, используем среднее расстояние от Земли до Солнца, равное <math>r=149,6\cdot {{10}^{6}}</math> км, и отношение массы Солнца к массе Земли <math>\mu=332 982</math>. В этом случае получаем величину «горба» около 16 см.

См. также

Напишите отзыв о статье "Прилив и отлив"

Примечания

↑ 1 2 Хайкин С. Э. Силы инерции и невесомость.— М.: «Наука».—1967.
↑ [bloknot.info/jose-de-acosta-historia-natural-y-moral-de-las-indias-parte-1/30/ José de Acosta. Historia natural y moral de las Indias. Capítulo XIV. Del flujo y reflujo del mar océano en Indias]
↑ Шулейкин В. В. Физика моря.— М.: Изд-во «Наука», Отделение наук о Земле АН СССР,— 1967.

Литература

Приливы и отливы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. — М.: ГИТТЛ, 1957
Шулейкин В. В. Физика моря. — М.: Изд-во «Наука», Отделение наук о Земле АН СССР, 1967
Войт С. С. Что такое приливы. Редколлегия научно-популярной литературы АН СССР.
Дуванин А. И. Приливы в море. — Л.: ГИМИЗ, 1960
Белонучкин В. [kvant.mccme.ru/1989/12/prilivnye_sily.htm Приливные силы] // Квант. — М., 1989. — № 12.

Ссылки

[www.wxtide32.com/ WXTide32 — свободно распространяемая программа для составления таблиц приливов]
[www.lhup.edu/~DSIMANEK/scenario/tides.htm D.E. Simanek, Tidal Misconceptions]
[sqlib.tumblr.com/post/101339255681/1963-i «Таблицы приливов на 1963 год. Том I. Воды Европейской части СССР»]

Отрывок, характеризующий Прилив и отлив

Толпа побежала за государем, проводила его до дворца и стала расходиться. Было уже поздно, и Петя ничего не ел, и пот лил с него градом; но он не уходил домой и вместе с уменьшившейся, но еще довольно большой толпой стоял перед дворцом, во время обеда государя, глядя в окна дворца, ожидая еще чего то и завидуя одинаково и сановникам, подъезжавшим к крыльцу – к обеду государя, и камер лакеям, служившим за столом и мелькавшим в окнах. За обедом государя Валуев сказал, оглянувшись в окно: – Народ все еще надеется увидать ваше величество. Обед уже кончился, государь встал и, доедая бисквит, вышел на балкон. Народ, с Петей в середине, бросился к балкону. – Ангел, отец! Ура, батюшка!.. – кричали народ и Петя, и опять бабы и некоторые мужчины послабее, в том числе и Петя, заплакали от счастия. Довольно большой обломок бисквита, который держал в руке государь, отломившись, упал на перилы балкона, с перил на землю. Ближе всех стоявший кучер в поддевке бросился к этому кусочку бисквита и схватил его. Некоторые из толпы бросились к кучеру. Заметив это, государь велел подать себе тарелку бисквитов и стал кидать бисквиты с балкона. Глаза Пети налились кровью, опасность быть задавленным еще более возбуждала его, он бросился на бисквиты. Он не знал зачем, но нужно было взять один бисквит из рук царя, и нужно было не поддаться. Он бросился и сбил с ног старушку, ловившую бисквит. Но старушка не считала себя побежденною, хотя и лежала на земле (старушка ловила бисквиты и не попадала руками). Петя коленкой отбил ее руку, схватил бисквит и, как будто боясь опоздать, опять закричал «ура!», уже охриплым голосом. Государь ушел, и после этого большая часть народа стала расходиться. – Вот я говорил, что еще подождать – так и вышло, – с разных сторон радостно говорили в народе. Как ни счастлив был Петя, но ему все таки грустно было идти домой и знать, что все наслаждение этого дня кончилось. Из Кремля Петя пошел не домой, а к своему товарищу Оболенскому, которому было пятнадцать лет и который тоже поступал в полк. Вернувшись домой, он решительно и твердо объявил, что ежели его не пустят, то он убежит. И на другой день, хотя и не совсем еще сдавшись, но граф Илья Андреич поехал узнавать, как бы пристроить Петю куда нибудь побезопаснее.

15 го числа утром, на третий день после этого, у Слободского дворца стояло бесчисленное количество экипажей. Залы были полны. В первой были дворяне в мундирах, во второй купцы с медалями, в бородах и синих кафтанах. По зале Дворянского собрания шел гул и движение. У одного большого стола, под портретом государя, сидели на стульях с высокими спинками важнейшие вельможи; но большинство дворян ходило по зале. Все дворяне, те самые, которых каждый день видал Пьер то в клубе, то в их домах, – все были в мундирах, кто в екатерининских, кто в павловских, кто в новых александровских, кто в общем дворянском, и этот общий характер мундира придавал что то странное и фантастическое этим старым и молодым, самым разнообразным и знакомым лицам. Особенно поразительны были старики, подслеповатые, беззубые, плешивые, оплывшие желтым жиром или сморщенные, худые. Они большей частью сидели на местах и молчали, и ежели ходили и говорили, то пристроивались к кому нибудь помоложе. Так же как на лицах толпы, которую на площади видел Петя, на всех этих лицах была поразительна черта противоположности: общего ожидания чего то торжественного и обыкновенного, вчерашнего – бостонной партии, Петрушки повара, здоровья Зинаиды Дмитриевны и т. п. Пьер, с раннего утра стянутый в неловком, сделавшемся ему узким дворянском мундире, был в залах. Он был в волнении: необыкновенное собрание не только дворянства, но и купечества – сословий, etats generaux – вызвало в нем целый ряд давно оставленных, но глубоко врезавшихся в его душе мыслей о Contrat social [Общественный договор] и французской революции. Замеченные им в воззвании слова, что государь прибудет в столицу для совещания с своим народом, утверждали его в этом взгляде. И он, полагая, что в этом смысле приближается что то важное, то, чего он ждал давно, ходил, присматривался, прислушивался к говору, но нигде не находил выражения тех мыслей, которые занимали его. Был прочтен манифест государя, вызвавший восторг, и потом все разбрелись, разговаривая. Кроме обычных интересов, Пьер слышал толки о том, где стоять предводителям в то время, как войдет государь, когда дать бал государю, разделиться ли по уездам или всей губернией… и т. д.; но как скоро дело касалось войны и того, для чего было собрано дворянство, толки были нерешительны и неопределенны. Все больше желали слушать, чем говорить. Один мужчина средних лет, мужественный, красивый, в отставном морском мундире, говорил в одной из зал, и около него столпились. Пьер подошел к образовавшемуся кружку около говоруна и стал прислушиваться. Граф Илья Андреич в своем екатерининском, воеводском кафтане, ходивший с приятной улыбкой между толпой, со всеми знакомый, подошел тоже к этой группе и стал слушать с своей доброй улыбкой, как он всегда слушал, в знак согласия с говорившим одобрительно кивая головой. Отставной моряк говорил очень смело; это видно было по выражению лиц, его слушавших, и по тому, что известные Пьеру за самых покорных и тихих людей неодобрительно отходили от него или противоречили. Пьер протолкался в середину кружка, прислушался и убедился, что говоривший действительно был либерал, но совсем в другом смысле, чем думал Пьер. Моряк говорил тем особенно звучным, певучим, дворянским баритоном, с приятным грассированием и сокращением согласных, тем голосом, которым покрикивают: «Чеаек, трубку!», и тому подобное. Он говорил с привычкой разгула и власти в голосе. – Что ж, что смоляне предложили ополченцев госуаю. Разве нам смоляне указ? Ежели буародное дворянство Московской губернии найдет нужным, оно может выказать свою преданность государю импературу другими средствами. Разве мы забыли ополченье в седьмом году! Только что нажились кутейники да воры грабители… Граф Илья Андреич, сладко улыбаясь, одобрительно кивал головой. – И что же, разве наши ополченцы составили пользу для государства? Никакой! только разорили наши хозяйства. Лучше еще набор… а то вернется к вам ни солдат, ни мужик, и только один разврат. Дворяне не жалеют своего живота, мы сами поголовно пойдем, возьмем еще рекрут, и всем нам только клич кликни гусай (он так выговаривал государь), мы все умрем за него, – прибавил оратор одушевляясь. Илья Андреич проглатывал слюни от удовольствия и толкал Пьера, но Пьеру захотелось также говорить. Он выдвинулся вперед, чувствуя себя одушевленным, сам не зная еще чем и сам не зная еще, что он скажет. Он только что открыл рот, чтобы говорить, как один сенатор, совершенно без зубов, с умным и сердитым лицом, стоявший близко от оратора, перебил Пьера. С видимой привычкой вести прения и держать вопросы, он заговорил тихо, но слышно: – Я полагаю, милостивый государь, – шамкая беззубым ртом, сказал сенатор, – что мы призваны сюда не для того, чтобы обсуждать, что удобнее для государства в настоящую минуту – набор или ополчение. Мы призваны для того, чтобы отвечать на то воззвание, которым нас удостоил государь император. А судить о том, что удобнее – набор или ополчение, мы предоставим судить высшей власти… Пьер вдруг нашел исход своему одушевлению. Он ожесточился против сенатора, вносящего эту правильность и узкость воззрений в предстоящие занятия дворянства. Пьер выступил вперед и остановил его. Он сам не знал, что он будет говорить, но начал оживленно, изредка прорываясь французскими словами и книжно выражаясь по русски. – Извините меня, ваше превосходительство, – начал он (Пьер был хорошо знаком с этим сенатором, но считал здесь необходимым обращаться к нему официально), – хотя я не согласен с господином… (Пьер запнулся. Ему хотелось сказать mon tres honorable preopinant), [мой многоуважаемый оппонент,] – с господином… que je n'ai pas L'honneur de connaitre; [которого я не имею чести знать] но я полагаю, что сословие дворянства, кроме выражения своего сочувствия и восторга, призвано также для того, чтобы и обсудить те меры, которыми мы можем помочь отечеству. Я полагаю, – говорил он, воодушевляясь, – что государь был бы сам недоволен, ежели бы он нашел в нас только владельцев мужиков, которых мы отдаем ему, и… chair a canon [мясо для пушек], которую мы из себя делаем, но не нашел бы в нас со… со… совета. Многие поотошли от кружка, заметив презрительную улыбку сенатора и то, что Пьер говорит вольно; только Илья Андреич был доволен речью Пьера, как он был доволен речью моряка, сенатора и вообще всегда тою речью, которую он последнею слышал. – Я полагаю, что прежде чем обсуждать эти вопросы, – продолжал Пьер, – мы должны спросить у государя, почтительнейше просить его величество коммюникировать нам, сколько у нас войска, в каком положении находятся наши войска и армии, и тогда… Но Пьер не успел договорить этих слов, как с трех сторон вдруг напали на него. Сильнее всех напал на него давно знакомый ему, всегда хорошо расположенный к нему игрок в бостон, Степан Степанович Апраксин. Степан Степанович был в мундире, и, от мундира ли, или от других причин, Пьер увидал перед собой совсем другого человека. Степан Степанович, с вдруг проявившейся старческой злобой на лице, закричал на Пьера: – Во первых, доложу вам, что мы не имеем права спрашивать об этом государя, а во вторых, ежели было бы такое право у российского дворянства, то государь не может нам ответить. Войска движутся сообразно с движениями неприятеля – войска убывают и прибывают… Другой голос человека, среднего роста, лет сорока, которого Пьер в прежние времена видал у цыган и знал за нехорошего игрока в карты и который, тоже измененный в мундире, придвинулся к Пьеру, перебил Апраксина. – Да и не время рассуждать, – говорил голос этого дворянина, – а нужно действовать: война в России. Враг наш идет, чтобы погубить Россию, чтобы поругать могилы наших отцов, чтоб увезти жен, детей. – Дворянин ударил себя в грудь. – Мы все встанем, все поголовно пойдем, все за царя батюшку! – кричал он, выкатывая кровью налившиеся глаза. Несколько одобряющих голосов послышалось из толпы. – Мы русские и не пожалеем крови своей для защиты веры, престола и отечества. А бредни надо оставить, ежели мы сыны отечества. Мы покажем Европе, как Россия восстает за Россию, – кричал дворянин. Пьер хотел возражать, но не мог сказать ни слова. Он чувствовал, что звук его слов, независимо от того, какую они заключали мысль, был менее слышен, чем звук слов оживленного дворянина. Илья Андреич одобривал сзади кружка; некоторые бойко поворачивались плечом к оратору при конце фразы и говорили: – Вот так, так! Это так! Пьер хотел сказать, что он не прочь ни от пожертвований ни деньгами, ни мужиками, ни собой, но что надо бы знать состояние дел, чтобы помогать ему, но он не мог говорить. Много голосов кричало и говорило вместе, так что Илья Андреич не успевал кивать всем; и группа увеличивалась, распадалась, опять сходилась и двинулась вся, гудя говором, в большую залу, к большому столу. Пьеру не только не удавалось говорить, но его грубо перебивали, отталкивали, отворачивались от него, как от общего врага. Это не оттого происходило, что недовольны были смыслом его речи, – ее и забыли после большого количества речей, последовавших за ней, – но для одушевления толпы нужно было иметь ощутительный предмет любви и ощутительный предмет ненависти. Пьер сделался последним. Много ораторов говорило после оживленного дворянина, и все говорили в том же тоне. Многие говорили прекрасно и оригинально. Издатель Русского вестника Глинка, которого узнали («писатель, писатель! – послышалось в толпе), сказал, что ад должно отражать адом, что он видел ребенка, улыбающегося при блеске молнии и при раскатах грома, но что мы не будем этим ребенком. – Да, да, при раскатах грома! – повторяли одобрительно в задних рядах. Толпа подошла к большому столу, у которого, в мундирах, в лентах, седые, плешивые, сидели семидесятилетние вельможи старики, которых почти всех, по домам с шутами и в клубах за бостоном, видал Пьер. Толпа подошла к столу, не переставая гудеть. Один за другим, и иногда два вместе, прижатые сзади к высоким спинкам стульев налегающею толпой, говорили ораторы. Стоявшие сзади замечали, чего не досказал говоривший оратор, и торопились сказать это пропущенное. Другие, в этой жаре и тесноте, шарили в своей голове, не найдется ли какая мысль, и торопились говорить ее. Знакомые Пьеру старички вельможи сидели и оглядывались то на того, то на другого, и выражение большей части из них говорило только, что им очень жарко. Пьер, однако, чувствовал себя взволнованным, и общее чувство желания показать, что нам всё нипочем, выражавшееся больше в звуках и выражениях лиц, чем в смысле речей, сообщалось и ему. Он не отрекся от своих мыслей, но чувствовал себя в чем то виноватым и желал оправдаться. – Я сказал только, что нам удобнее было бы делать пожертвования, когда мы будем знать, в чем нужда, – стараясь перекричать другие голоса, проговорил он. Один ближайший старичок оглянулся на него, но тотчас был отвлечен криком, начавшимся на другой стороне стола. – Да, Москва будет сдана! Она будет искупительницей! – кричал один. – Он враг человечества! – кричал другой. – Позвольте мне говорить… Господа, вы меня давите…

В это время быстрыми шагами перед расступившейся толпой дворян, в генеральском мундире, с лентой через плечо, с своим высунутым подбородком и быстрыми глазами, вошел граф Растопчин. – Государь император сейчас будет, – сказал Растопчин, – я только что оттуда. Я полагаю, что в том положении, в котором мы находимся, судить много нечего. Государь удостоил собрать нас и купечество, – сказал граф Растопчин. – Оттуда польются миллионы (он указал на залу купцов), а наше дело выставить ополчение и не щадить себя… Это меньшее, что мы можем сделать! Начались совещания между одними вельможами, сидевшими за столом. Все совещание прошло больше чем тихо. Оно даже казалось грустно, когда, после всего прежнего шума, поодиночке были слышны старые голоса, говорившие один: «согласен», другой для разнообразия: «и я того же мнения», и т. д. Было велено секретарю писать постановление московского дворянства о том, что москвичи, подобно смолянам, жертвуют по десять человек с тысячи и полное обмундирование. Господа заседавшие встали, как бы облегченные, загремели стульями и пошли по зале разминать ноги, забирая кое кого под руку и разговаривая. – Государь! Государь! – вдруг разнеслось по залам, и вся толпа бросилась к выходу. По широкому ходу, между стеной дворян, государь прошел в залу. На всех лицах выражалось почтительное и испуганное любопытство. Пьер стоял довольно далеко и не мог вполне расслышать речи государя. Он понял только, по тому, что он слышал, что государь говорил об опасности, в которой находилось государство, и о надеждах, которые он возлагал на московское дворянство. Государю отвечал другой голос, сообщавший о только что состоявшемся постановлении дворянства. – Господа! – сказал дрогнувший голос государя; толпа зашелестила и опять затихла, и Пьер ясно услыхал столь приятно человеческий и тронутый голос государя, который говорил: – Никогда я не сомневался в усердии русского дворянства. Но в этот день оно превзошло мои ожидания. Благодарю вас от лица отечества. Господа, будем действовать – время всего дороже… Государь замолчал, толпа стала тесниться вокруг него, и со всех сторон слышались восторженные восклицания. – Да, всего дороже… царское слово, – рыдая, говорил сзади голос Ильи Андреича, ничего не слышавшего, но все понимавшего по своему. Из залы дворянства государь прошел в залу купечества. Он пробыл там около десяти минут. Пьер в числе других увидал государя, выходящего из залы купечества со слезами умиления на глазах. Как потом узнали, государь только что начал речь купцам, как слезы брызнули из его глаз, и он дрожащим голосом договорил ее. Когда Пьер увидал государя, он выходил, сопутствуемый двумя купцами. Один был знаком Пьеру, толстый откупщик, другой – голова, с худым, узкобородым, желтым лицом. Оба они плакали. У худого стояли слезы, но толстый откупщик рыдал, как ребенок, и все твердил: – И жизнь и имущество возьми, ваше величество! Пьер не чувствовал в эту минуту уже ничего, кроме желания показать, что все ему нипочем и что он всем готов жертвовать. Как упрек ему представлялась его речь с конституционным направлением; он искал случая загладить это. Узнав, что граф Мамонов жертвует полк, Безухов тут же объявил графу Растопчину, что он отдает тысячу человек и их содержание. Старик Ростов без слез не мог рассказать жене того, что было, и тут же согласился на просьбу Пети и сам поехал записывать его. На другой день государь уехал. Все собранные дворяне сняли мундиры, опять разместились по домам и клубам и, покряхтывая, отдавали приказания управляющим об ополчении, и удивлялись тому, что они наделали.

Наполеон начал войну с Россией потому, что он не мог не приехать в Дрезден, не мог не отуманиться почестями, не мог не надеть польского мундира, не поддаться предприимчивому впечатлению июньского утра, не мог воздержаться от вспышки гнева в присутствии Куракина и потом Балашева. Александр отказывался от всех переговоров потому, что он лично чувствовал себя оскорбленным. Барклай де Толли старался наилучшим образом управлять армией для того, чтобы исполнить свой долг и заслужить славу великого полководца. Ростов поскакал в атаку на французов потому, что он не мог удержаться от желания проскакаться по ровному полю. И так точно, вследствие своих личных свойств, привычек, условий и целей, действовали все те неперечислимые лица, участники этой войны. Они боялись, тщеславились, радовались, негодовали, рассуждали, полагая, что они знают то, что они делают, и что делают для себя, а все были непроизвольными орудиями истории и производили скрытую от них, но понятную для нас работу. Такова неизменная судьба всех практических деятелей, и тем не свободнее, чем выше они стоят в людской иерархии.

wiki-org.ru

Прилив и отлив моря. Отлив и прилив