Математика — царица всех наук Гаусс Карл Фридрих
Математика — наука, исторически основанная на решении задач о количественных и пространственных соотношениях реального мира путём идеализации необходимых для этого свойств объектов и формализации этих задач. Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
Как правило, люди думают, что математика — это всего лишь арифметика, то есть изучение чисел и действий с их помощью, например, умножения и деления. На самом деле математика — это намного больше. Это способ описать мир и то, как одна его часть сочетается с другой. Взаимоотношения чисел выражаются в математических символах, которые описывают Вселенную, в которой мы живем. Любой нормальный ребенок может преуспевать в математике, потому что «ощущение числа» — это врожденная способность. Правда, для этого нужно приложить некоторые усилия и затратить немного времени.
Умение считать — это еще не все. Ребенку необходимо уметь хорошо выражать свои мысли, чтобы понимать задачи и устанавливать связи между фактами, которые хранятся в памяти. Для того чтобы выучить таблицу умножения, нужны память и речь. Именно поэтому некоторым людям с поврежденным мозгом трудно умножать, хотя другие виды счета не представляют для них сложности.
Для того чтобы хорошо знать геометрию и разбираться в форме и пространстве, требуются и другие виды мышления. С помощью математики мы решаем в жизни проблемы, например, делим шоколадку поровну или находим нужный размер ботинок. Благодаря знанию математики ребенок умеет копить карманные деньги и понимает, что можно купить и сколько денег тогда у него останется. Математика — это еще и способность отсчитать нужное количество семян и посеять их в горшочек, отмерять нужное количество муки для пирога или ткани на платье, понять счет футбольной игры и множество других повседневных дел. Везде: в банке, в магазине, дома, на работе — нам необходимо умение понимать числа, формы и меры и обращаться с ними. Числа — это только часть особого математического языка, а лучший способ выучить любой язык — это применять его. И начинать лучше с ранних лет.
Обычно идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное к математике положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе существует много различных определений математики.
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного математика — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. Пространство Rn, при n>3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях.
Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Видео-лекция Смирнова С.К. и Ященко И.В. «Что такое математика»:
Похожая информация:informat.name
Слово «математика» тоже пришло из древнегреческого языка. Сейчас мы прочно знаем, что математика – это наука о числах и количествах, о структурах, порядках и отношениях, что в нее входят арифметика и алгебра, геометрия и тригонометрия, и т.д. Однако очень интересно то, что в Древней Греции слово τό μάθημα (mathēma) первоначально значило просто знание, учение или науку вообще, то есть, любую науку. И, например, словосочетание τὰ παίδων μαθήματα, встречающееся у Платона, значит знания, приобретенные в детстве, а не детскую математику или подсчет детей.
Это древнегреческое слово является однокоренным с глаголом μανθάνω (manthanō) – учиться, изучать, понимать. А существительное ὁ μαθητής (mathētēs), встречающееся и в Новом Завете, обозначает вовсе не математика, а ученика или последователя какого-то учителя или учения.
В связи с такой любопытной этимологией я хотел бы отметить две очень важные, как мне кажется, вещи.
1) Во-первых, конечно, есть четкая логика в том, что слово, значившее сначала науку или знание вообще, потом закрепилось за наукой математикой. Ведь математика очень долго считалась образцом строгости и научности для всех других наук, своего рода королевой в царстве знаний. Например, «Начала» древнегреческого математика Евклида больше двух тысячелетий служили образцом для любого научного труда, а классическая евклидова геометрия считалась единственно возможной геометрией.
Галилео Галилей, заложивший основы математической физики, говорил, что книга природы написана на языке математики, и что надо уметь ее читать. Философ Спиноза строил свою знаменитую «Этику» more geometrico, т.е., по евклидову образцу – с аксиомами, теоремами, их доказательствами и леммами. А Карл Маркс однажды сказал даже, что любая наука лишь тогда станет совершенной, когда ей удастся воспользоваться математикой.
Современную физику нельзя представить нематематической. Знаменитый физик, лауреат Нобелевской премии по физике 1979 года Стивен Вайнберг говорит, что суть современной физики – по-прежнему количественное понимание явлений. И даже в квантовой физике то, что «материя исчезла», что стало совершенно непонятно, что же такое атом и его составные части (волны это или частицы), что они совершенно непредставимы и неизобразимы, эту неуловимость вещества поставили под численный учет и контроль (принцип неопределенности Гейзенберга). Современная неклассическая физика все равно измеряет неизмеримое, потому что она в принципе не может перестать считать, измерять и смотреть на мир через призму количественных отношений.
Однако где-то со второй половины XIX века все более и более ясным становилось то, что и математика тоже не является безусловным и строгим знанием, что ее основания тоже проблематичны. Кроме евклидовой геометрии были открыты геометрии неевклидовы – геометрии Лобачевского и Римана. С открытием теории относительности даже обнаружилось, что неевклидова геометрия согласно ей более адекватно описывает свойства космоса, мира в целом.
К началу ХХ века в математике также обнаружился кризис ее оснований, как и в других науках. Например, были обнаружены логико-математические парадоксы, которые сделали явной невыполнимость такой программы исследований оснований математики, которая получила название логицизма, то есть сведения всех математических положений к основоположениям логики. Поэтому доказать, что математика является логически непротиворечивой системой, не удалось. Самым знаменитым логико-математическим парадоксом, не имеющим решения, является парадокс Рассела. В более легкой формулировке он известен как парадокс брадобрея:
Единственному деревенскому брадобрею приказали: «Брить всякого, кто сам не бреется, и не брить того, кто сам бреется». Кто побреет брадобрея, и как ему поступить с сами собой? Брить или нет?
Словом, математика разделила судьбу всех других наук – от веры в их незыблемость и истинность до осознания их проблематичности и ненадежности самых главных основ. В ней произошло то, что можно назвать утратой определенности. Именно так – «Математика: утрата определенности» – называется блестящая научно-популярная книга о трудном историческом пути математики как науки известного американского математика Мориса Клайна.
Как он писал в «Введении», «эта книга – горестный рассказ о бедствиях, выпавших на долю математики – наиболее древнего и не имеющего себе равных творения людей, плода их неустанных и многообразных усилий, направленных на использование способности человека мыслить. Можно также сказать, что эта книга на общедоступном уровне повествует о расцвете и закате величия математики…
В настоящий момент положение дел в математике можно обрисовать примерно так. Существует не одна, а много математик, и каждая из них по ряду причин не удовлетворяет математиков, принадлежащих к другим школам. Стало ясно, что представление о своде общепринятых, незыблемых истин — величественной математике начала XIX в., гордости человека – не более чем заблуждение. На смену уверенности и благодушию, царившим в прошлом, пришли неуверенность и сомнения в будущем математики. Разногласия по поводу оснований самой “незыблемой” из наук вызвали удивление и разочарование (чтобы не сказать больше). Нынешнее состояние математики – не более чем жалкая пародия на математику прошлого с ее глубоко укоренившейся и широко известной репутацией безупречного идеала истинности и логического совершенства».
2) Второе обстоятельство, связанное с математикой, имеет отношение к тому, что христианская вера – это именно вера, к ней неприложимы рациональные критерии, действующие в научном знании.
Ведь самые основы христианства – учение о Боге-Троице – вступают в полное противоречие с самыми элементарными математическими положениями. Ибо как можно рационально понять и осмыслить то, что Бог един и одновременно троичен?
Что Он – един в Трех Лицах? Что Святая Троица – Бог-Отец, Бог-Сын и Бог-Дух Святой – это три Лица Единственного и Единого Бога? Что три здесь равно одному, единице? Это входит в полное противоречие с нашими элементарными умственными и математическими навыками и привычками, с правилами счета, которые любой человек осваивает, как правило, еще в дошкольном возрасте.
Кстати, интересно и показательно, что великий английский физик Исаак Ньютон, основоположник математизированной классической физики в молодости учился в Кембриджском университете в колледже Святой Троицы и даже подумывал стать священником, но в итоге решил не связывать свою судьбу со священническим служением именно из-за сомнений в учении о Троице. Да и позже он активно высказывал свои антитринитарские воззрения.
Так что, наверно, прав был Тертуллиан, автор знаменитого «Верую, ибо абсурдно», и не менее знаменитого риторического вопроса «Что общего между Афинами и Иерусалимом?» В данном случае он просто выразил то, как следует грамотно думать о христианской вере, то, что она не знание, а именно вера, которая в своей основе радикально противоречит нашему логическому и математическому рацио, рассудку. Верить можно только в то, что не можешь знать сам по себе.
www.pravoslavie.ru
Выделим четыре признака науки.
Первый — наличие познаваемого объекта. Второй — истинность суждений о нем, проверяемая опытом. Третий — всеобщность (универсальность) и обязательность установленных закономерностей. Четвертый — системность, последовательность вытекающих друг из друга понятий.
Только одновременная реализация всех этих признаков и определяет научность известного результата познания.
Слово «математика» — от греческого mathema — «наука». Однако рассмотрим математику с позиции четырех признаков науки.
Этот род человеческой деятельности не соответствует первому критерию — нет объекта исследования. Не соответствует и второму — ее выводы опытом не проверяются.
Математики при оценке своих работ полагаются на свой «вкус», говорят: «Красивое решение!» А это уже искусство.
Не поймите меня превратно. Я нисколько не принижаю значения математики как языка науки. Чем более наука формализована, тем она продуктивнее в эвристическом смысле.
Нет докторов и кандидатов математических наук — есть физико-математических. Объекты для ее приложений поставляют физика (как наиболее формализованная), геофизика, архитектура, некоторые разделы теоретической химии (например, квантовая, молекулярный дизайн), математические биология и экономика. В рамках уже этих наук работает и опыт как критерий истины.
Наименее формализованы большинство разделов химии, геология и практически все гуманитарные науки. Хотя и в них математические методы широко применяются: в лингвистическом анализе, социологии, демографии и т. п. Например, математику А. Н. Колмогорову принадлежит первое научное определение лингвистического понятия падежа как класса эквивалентных семантических состояний.
Огромен вклад математики в сращивание естественных наук с гуманитарными путем использования в них дедуктивных методов и математического моделирования с применением многих разделов математики — от элементарной алгебры до топологии.
Открыты и неформализованные естественные законы (Периодический закон Д. И. Менделеева в виде таблицы, 230 групп симметрии кристаллов Е. С. Федорова в виде пространственных моделей, закон гомологических рядов в наследственной изменчивости организмов Н. И. Вавилова). В их основе лежат фундаментальные свойства материи — в Периодической системе это заряд ядра атома. Для сложных систем законов, не имеющих математического выражения, должно быть существенно больше.
Наука начинается там, где появляется измерение. Но не надо путать измерение и математику. Математика — это строгий язык, но общаться можно и нестрогими языками жестов, образов (живопись, музыка). В любых картах — географических, геологических и прочих — минимум математики и максимум свернутой информации в виде образов.
Так что учите языки, в том числе и математический.
Личное жизненное наблюдение: специалисты, владеющие математикой, легко самостоятельно изучают иностранные языки.
shkolazhizni.ru
«Троицкий вариант» №2(146), 28 января 2014 года
В новогодние каникулы 2014 года Владимир Андреевич Успенский любезно согласился встретиться и поговорить с Михаилом Гельфандом. Мы публикуем расшифровку стенограммы этой беседы, подвергшуюся минимальному редактированию. Курсивом показаны места, выделенные в разговоре интонацией.
В ходе интервью В. А. Успенским было рассказано о двух его любимых лекторах, П. С. Новикове и И. М. Гельфанде. Этот рассказ помещен в конце интервью.
— Насколько я понимаю, у Вас занятия математикой всегда происходили на границе математики и языка, это был в каком-то смысле лингвистический фланг математики.
— Я не могу сказать, что это происходило на границе математики и лингвистики. Скорее, это был логический фланг. Все-таки математикой я начал заниматься существенно раньше, чем лингвистикой.
Есть такой уважаемый мною человек, Евгений Абрамович Бунимович. В ноябре 2013 года, на церемонии вручения премии «Просветитель», членом жюри которой он состоит, он сказал: «В России есть всего два математика, которые считают, что математика — это гуманитарная наука: это Владимир Андреевич Успенский и я».
— Я не математик, но я тоже так считаю.
— Правильно. Но, скажем, великий Арнольд — наши ранги как математиков несопоставимы, так что я испытываю неловкость, возражая ему, — считал, что математика это часть физики.
— Я ровно про это и хотел спросить.
— Если математика — часть физики, то с таким же успехом она — часть психологии. Потому что всё происходит в голове у человека. Возьмите такую науку, как теория чисел. Никаких аксиом там нет. Я плохо отношусь к Виноградову [1], как и большинство приличных людей, но его книжку «Основы теории чисел» читал с огромным удовольствием.
Она начинается из ничего и доходит до некоторых высот. Потому что в головах имеется некоторое представление о натуральном числе, и если один человек сидит здесь, а другой — в Новой Зеландии, то это представление у них будет одинаковым: ведь выводы, к которым они приходят, совпадают. Значит, это свойство человеческой психологии. Некоторые выводят из этого существование Бога. Об этом я не берусь судить, но сам факт такого единства достоин внимания.
— Недавно в Science была статья, что восприятие малых количеств у людей в голове находится вовсе не в том месте, где последовательный индуктивный счет. И имеется пространственный градиент активности в соответствующей зоне коры головного мозга в зависимости от числа предъявленных картинок, от одного до семи [2].
— Конечно, а дальше уже «много». Это отражается в языке: два, три, четыре стула, но пять стульев. Мой любимый тезис, что бесконечность — это аппроксимация конечного сверху. Иногда проще сказать не «восемь септильонов», а «бесконечно».
— «Много» начинается там, где не видно сразу, а надо считать, показывая пальцем.
— Вы затронули интересный вопрос, мне его иногда задают важные коллеги, — откуда начинается натуральный ряд, с ноля или с единицы? Дело в том, есть два понятия натурального ряда. Есть количественное, оно охватывает ноль: «Сколько здесь крокодилов? — Ноль», а есть «считательное»: если пересчитывать крокодилов, то, конечно, будет «раз, два, три...».
— Но большинство математиков все-таки идут от физики. Владимир Игоревич Арнольд, Юрий Иванович Манин [3], Израиль Моисеевич <Гельфанд>...
— Откуда идет большинство — это я не знаю. Египетская математика идет от прикладных задач, как пирамиды строить.
— То есть, это, скорее, физическая линия.
— Да, но греческая математика уже идет от высоких воспарений. Все-таки европейская математика происходит из Греции, а не из Египта. Пифагор — несоизмеримость отрезков [4], на хрен она, вообще говоря, была грекам нужна для их физики? А это великое открытие.
— Но если в европейской математике есть, условно, египетская физическая линия и греческая психологическая.
— Я бы сказал, психолого-эстетическая.
— ... то как в других математических культурах?
— Откуда же мне знать?
— Вы не пытались смотреть?
— Для этого нужно быть специалистом по истории математики.
— Вам никогда не хотелось?
— Хотелось. История математики — это чрезвычайно интересная наука, находящаяся повсеместно на довольно низком уровне. По следующей причине: ею занимаются люди, иногда вполне неглупые, но, как правило, те, у кого не получалась математика. Я с этим столкнулся на следующем примере. Когда мы с А. Л. Семёновым писали книжку про алгоритмы [5], мне нужно было узнать, у кого появилось понятие алгоритма — не слово (все знают про Аль-Хорезми [6]), а понятие алгоритма как описания процесса, который не ограничен в числе шагов, но приводит к результату.
На ответ я наткнулся почти случайно. Впервые это понятие появилось у Эмиля Бореля в 1912 году, но никто об этом не знал, потому что появилось оно в статье Бореля об определенном интеграле. Там он писал о «вычислениях, которые можно реально осуществить», подчеркивая при этом: «Я намеренно оставляю в стороне большую или меньшую практическую деятельность; суть здесь та, что каждая из этих операций осуществима в конечное время при помощи достоверного и недвусмысленного метода». Специалисты по математическому анализу, интересующиеся понятием интеграла, это прочли и пропустили мимо. А специалисты по теории алгоритмов в такую литературу не заглядывают. А ведь Борель в точности определил, что такое алгоритм.
— Примеры алгоритмов были и раньше.
— Примеры — разумеется. Я говорю про понятие, это большая разница. Конечно, у Аль-Хорезми были описания, как что-то там складывать...
— Или европейские математики, которые друг с другом соревновались в решении разных типов кубических уравнений.
— Задачи на построение — это по существу тоже алгоритм.
— Раз так, у Евклида не найдется строгого списка разрешенных операций и их последовательных комбинаций?
— Не найдется.
—А если широко на это посмотреть?
— Если посмотреть очень широко, да еще с современных позиций, то, возможно, из книг Евклида можно извлечь такой список. Осознавал ли его Евклид, неизвестно.
— Еще о классификации наук. Если считать, что математика — гуманитарная наука, то не является ли лингвистика — естественной наукой?
— Нет.
— Именно лингвистика, не филология.
— Если так, это правильный вопрос. Тогда да, согласен, в значительной степени является. Я считаю, что главная беда лингвистики — что она оказалась склеенной с литературоведением. Как сиамские близнецы. Что ее губит.
— Очень многие хорошие математики, которых я мог наблюдать или про которых слышал, много и в каком-то смысле глубоко слушали музыку. Израиль Моисеевич, Манин.
— Колмогоров.
— Музыкальный клуб на мехмате.
— Да, Александров.
— В моем поколении Максим Концевич...
— И что?
— Это правильное наблюдение?
— Правильное.
— Не связано ли это с тем, что одни и те же структуры мозга работают?
— Откуда же мне знать?
— А если фантазировать?
— С таким же успехом это может быть связано с тем, что работают противоположные структуры и происходит отдых. Можно сделать такой вывод и написать несколько диссертаций, а можно сделать другой вывод и тоже написать несколько диссертаций.
— Сейчас, видимо, можно приложить электроды и померить, какие области работают там и там. Меня удивляет, что этого никто не сделал.
— В мае 2004 года я побывал в Провиденсе, куда меня привезла мой друг Таня Корельская с целью посмотреть церемонию выпуска бакалавров Брауновского университета. Дело в том, что среди тех, на кого надели мантию, была ее старшая дочь Ксения. Таня привела меня в дом Вашего отца, которого я знаю с его 11 лет. Там я был напоен лучшей водкой, которую я когда-либо пил, и которую я с тех пор не могу ни забыть, ни найти [7]. А Ксения, занимавшаяся нейролингвистикой, привела меня в одну из университетских лабораторий, где мне показали на экране компьютера, как меняется приток крови к различным участкам мозга при произнесении тех или иных слов. Это, конечно, более грубо, чем электроды. Вот Вы — доктор биологических наук — сделайте.
— Я не тех биологических наук доктор.
— Ну, найдите кого-нибудь, кто сделает.
— А Вы слушаете музыку? Насколько это для Вас существенно?
— У меня с музыкой очень плохо, я об этом очень сожалею. Андрей Николаевич Колмогоров пытался меня приучить, что-то объяснял. Например, он мне объяснил вещь, которую я до него не понимал. Я не любил пение; как говорила моя теща, «я не люблю, когда при мне поют», — вот это мне было очень понятно. Он мне объяснил, что это такой музыкальный инструмент. Есть виолончель, есть фортепиано, а есть человеческий голос. Но я задал ему вопрос, на который он не смог ответить: «А слова-то зачем? Я их всё равно разобрать не могу».
— У Баха понятно, зачем.
— Это религиозные гимны, тут понятно, зачем.
— У Баха была целая риторическая система [8].
— Это другое дело, тут слова, которые иллюстрируются музыкой. А я помню арию Орфея «Потерял я Евридику, Евридики нет со мной», которую на виниловой пластинке мне ставил Колмогоров. Он честно пытался приучить меня к музыке. Андрей Николаевич меня должен был выгнать за эту неспособность, но терпел. Я сам себя в этом смысле считаю человеком патологическим. Это что-то вроде дислексии — я слышу по радио музыку, я понимаю, что я эту музыку много раз слышал и ее люблю, но запомнить, кто это и что это, я не в состоянии.
— Это другое. Вот я, скажем, лица людей не помню. И не связываю с именами. Но саму мелодию помните?
— Воспроизвести, конечно, не могу. Но я помню, что я эту мелодию много раз слышал, она мне нравится, но что это. Единственное, что я могу опознать, — это «Болеро» Равеля, причем не само «Болеро», а ритм барабана [9] — я его с трудом, но выучил.
Ну, подождите. Многие крупные математики, тот же Колмогоров, занимались усиленно спортом. Нет, не спортом, а именно физической культурой.
— Кажется, меньше. И потом, это их не выделяет из других ученых. А вот любовь к серьезной музыке — это уже специфично для математиков.
— Интересно, да.
— Опять, если бы были под рукой хорошие социологи, можно было бы их на это напустить.
— Чем отличается хороший математик от плохого? В чем разница во внутренних ощущениях и в способах обращения с материалом?
— Откуда же я знаю? Я же не хороший математик, я только со стороны могу смотреть. Есть несколько жанров математика. Когда-то мне Колмогоров говорил, что может быть очень хорошая работа, в которой теорем почти не доказывается, но вводится система понятий, которая чрезвычайно важна. Сюда же, видимо, относятся те, кто открывает новые теории. Третьи — те, кто решает задачи, которые стояли много лет, в узкой области.
Вот, опять, Виноградов — он хороший математик или нет? Наверное, сильный, и даже очень сильный, хотя и «узкий». Конечно, было бы лучше, если бы не делали вид, что он решил проблему Гольдбаха [10], которую он не решил. Но то, что он действительно решил в этой проблеме, достойно всяческого уважения. Так что есть разные математики. Что-то должно реализоваться: или умение решать сложную проблему, или придумывать новые теории, или создавать новую систему понятий.
— Я бы еще четвертое добавил — умение видеть связи между далекими областями.
— Вы правы. То, что умел делать Ваш великий дед.
— Я из воспоминаний о нем это и узнал — я не сам это придумал. Поскольку я вообще никакой не математик, хотя тоже мехмат заканчивал.
Когда я наблюдал математически сильных людей, на моем курсе и вокруг, у меня всегда было ощущение, что они умеют обращаться с понятиями, для которых у меня нет соответствующей машинки в голове. Пока можно было формально писать — я чисто алгебраически это делал, но как только чуть выходило за рамки, оказывалось, что я просто не умею про это думать.
— Думаю, Вы не по адресу. Вам надо бы взять какого-нибудь сильного математика, Манина, например.
— Я разговаривал с Юрием Ивановичем [3]. Это не помогает. Они в этот момент начинают, как поэты, разговаривать образами.
— Колмогоров, на моей памяти не меньше двух раз, обращал внимание вот на что. Математик, когда он думает, шевелит руками, пальцами. Он явно геометризирует какие- то мысленные конструкции. Колмогоров считал, что если изучить эти движения, то можно что-то понять в отношении мышления математика. Кто-то сказал, не помню кто, что математика берет образы несуществующие и обращается с ними, как с существующими. «Возьмем паракомпакт и выберем в нем точку» — что, как, где возьмем? Как выберем?
— Тогда это возвращает нас к разговору про математику и музыку. Альфред Шнитке говорил, что, когда он пишет музыку, он записывает то, что уже знает. Он не сочиняет последовательно — первую часть, потом вторую, — нет, у него имеется некоторый цельный образ, и его задача, как композитора, наиболее адекватно передать этот образ теми средствами, которые есть в его распоряжении.
— Когда математик пишет статью, он, конечно, в голове ее всю уже написал. Технических деталей может не хватать, но всё уже понятно.
— Откуда берутся ошибки в математике? Ошибочные гипотезы — сбой этого механизма? Неправильная картинка в голове возникла?
— Конечно. Но она — мощный двигатель прогресса. Вот, например, у Колумба была ошибочная гипотеза, что если плыть на запад, то там сразу Индия.
— Это пример не совсем про то; тут уж очень конкретно. Есть примеры, когда такие ошибки сильно продвинули математику?
— Убежден, что есть... (пауза). Ну вот, у великого математика Анри Лебега [11] была неправильная теорема, которую он опубликовал. Из ее опровержения возникла дескриптивная теория множеств. Фундаментальный вклад в эту теорию внес Николай Николаевич Лузин, создатель московской математической школы. У Лузина была книга [12], первоначально, в 1930 году, изданная в Париже по-французски с лестным предисловием Лебега.
Она потом два раза, отдельным изданием в 1953 году и во втором томе собрания сочинений Лузина в 1957 году, выходила в СССР в русском переводе, и оба раза обходились без предисловия Лебега. Это само по себе замечательно — кто такой Лебег, чтобы на него тратить время и бумагу. Про издание 1953 года всё понятно: оно готовилось еще при жизни Сталина, в период инициированной им борьбы с «низкопоклонством перед Западом». В издание 1957 года предисловие, думается, не было включено по причине традиционного издательского консерватизма.
Русский перевод предисловия удалось опубликовать лишь в 1985 году в связи со столетием Лузина [13]. Так вот, в этом предисловии было сказано: «Источником всех проблем, о которых пойдет здесь речь, послужила грубая ошибка в моем Мемуаре об аналитически представимых функциях. Плодотворная ошибка, меня просто вдохновило ее совершить». И далее: «Доказательство было простым, коротким, но неверным».
Это вот про что. Сначала на прямой — вы начинаете с отрезков, а дальше применяются три операции: дополнение, объединение счетного числа множеств и пересечение счетного числа множеств. Всякое множество, которое можно получить в результате, называется борелевским. На плоскости — аналогично, только начинаем с прямоугольников. А дальше вопрос: проекция плоского борелевского множества на прямую — это борелевское множество или нет? Лебегу было очевидно, что борелевское, и он это доказал и сделал из этого глубочайшие философские выводы, что математический анализ замкнут сам в себе, потому что за пределы борелевских множеств нельзя никуда выйти.
Дальше была драматическая история — в России на семинаре Лузина была обнаружена ошибка. У Лузина был выдающийся ученик, Суслин [14], который построил пример борелевского множества, проекция которого не борелевская. Сейчас проекции борелевских множеств называют суслинскими или А-множествами, Лузин называл их аналитическими. Им посвящена целая книга [12], от которой и пошла современная дескриптивная теория множеств.
Это пример не просто неправильной гипотезы, а неправильной теоремы, которая послужила толчком к созданию целого направления математики.
— Разговор про основы матанализа подводит еще к одному сюжету. Ясно, что многим нематематикам, условно говоря, филологам и биологам, нужна математика, и их надо ей учить.
—Ну, филологам вряд ли... Разве что статистика для стиховедения.
— Лингвистам.
— Лингвистам — да. Биологам — конечно.
—Теперь — для чего она им нужна? Первое соображение — тривиальное. Скажем, всем нужна статистика; это часть математики. Биологам нужны дифференциальные уравнения.
— Это у нас математическая статистика — часть математики. На Западе математическая статистика и теория вероятности образуют отдельный раздел науки, по объему равный математике, а то и превосходящий ее.
— Везде на Западе или только в США?
— Точно не знаю.
— Если США, то понятно, почему так.
— Да, из практических соображений. Страхование и так далее.
— Ну вот, первое, чему надо учить — это, грубо говоря, набор навыков, в каком-то смысле инженерных. А вторая причина — это то, что математика «ставит» мозги. Люди должны понимать смысл логических утверждений, понимать, что он может сильно поменяться от изменения порядка слов, что кванторы нельзя переставлять. «Для любого эпсилон существует дельта такая, что...» и «существует такая дельта, что для любого эпсилон... » — это существенно разные вещи.
— Это главное.
—Конечно. Но правильно ли учить этому на материале классического анализа, на языке эпсилон-дельта? Или сейчас для этого стоит брать какой-нибудь другой раздел математики? Я смотрел программу экзамена на нашем факультете биоинформатики. Вершиной там была лемма о компактности шара.
— Это им не нужно. Это и на мехмате бывает сложно первокурсникам.
В России всюду поступают так. Берут мехматское образование и в разных местах его урезают, иногда сильно, иногда слабо, иногда, скажем, на ВМК [15], оставляют почти такое же. На мехмате понятно, зачем эпсилон-дельта: математический анализ нужно профессионально выучить.
Учат всюду неправильно.
— А как правильно?
— Как правильно, я не знаю. Прежде всего, надо правильно обозначить цели. Может быть, цель — научить логике? Я много лет преподавал математическую логику лингвистам... Ну, например, что является отрицанием утверждения «в этой аудитории каждый из студентов знает хотя бы один из двух языков — баскский или чукотский» [16]? Вот на таких примерах надо учить.
— Казалось бы, это ничем не отличается от эпсилон-дельта.
— Правильно. Это не отличается по целям и по способу, но это гораздо нагляднее.
— Это для лингвистов. А для биологов?
— Для всех. Какая разница?
—Может быть, биологов вообще не надо этому учить, потому что не видно, где бы в биологии это было существенно. Лингвисты должны видеть структуру предложения...
— Все говорят на языке — все должны видеть структуру.
— Мне казалось, что биологов надо учить на материале комбинаторики. Понять разницу между схемой с возвращением и схемой без возвращения [17] — это примерно такое же интеллектуальное усилие, как понять порядок кванторов.
— Не совсем. Вы правы, что это усилие такой же трудности. Но содержательно — я не согласен. Чему надо учить биологов — это Вам виднее. Это Вам виднее. Определять это должны не математики, которые всех хотят учить всему, а те, кого учат. Чему надо учить — неизвестно. Чему в школе надо учить, не знает никто.
— Возможно, я не с того конца зашел. Есть две области математики, которые имеют дело с простыми и очень естественными объектами: логика, которая фактически работает с языком, и комбинаторика, которая имеет дело с предметами.
— Комбинаторика имеет дело с множествами. Стало быть, появляются кванторы. Ну, вот совсем простая задача: в Швейцарии каждый знает не менее трех из четырех официальных языков. Доказать, что любые три швейцарца могут объясниться на общем языке. Это и комбинаторика, и логика.
— Видимо, правильный курс должен состоять из таких вещей. Если считать, что есть цель преподавания математики «естественным» ученым, помимо инженерной...
— Ломоносов говорил, я это по своей брошюре [18] цитирую: «Математику уже за то любить надо, что она ум на место ставит».
— ... из чего такой курс должен состоять?
— Вы ошибочно полагаете, что я знаю. Но я согласен, что комбинаторика там должна занимать большое место. В частности, такого сорта задачи: имеются монеты, некоторые из них фальшивые, и нужно сколькими- то взвешиваниями определить, какие. Разные схемы могут быть.
— Все-таки, это, скорее, про то, как надо учить математике в биологической школе. Это уровень интересных задач и общего развития. А я спрашиваю, надо ли преподавать что-то систематическое.
— Опять — нужно подойти с другого конца. Кто-то мне давно сказал, что «надо» — слово бессмысленное. Правильно — «надо для чего-то». Вот и решайте.
Вот Лузин, когда учился в гимназии, «поначалу обнаружил полную неспособность к математике в той форме, в которой она преподавалась (заучивание правил и действия по шаблонам)» [19].
В моей жизни были два совершенно гениальных лектора. Походы на их лекции являлись полным наслаждением. Причем, я очень хорошо помню, что, хотя ходить было наслаждением, как на концерт, если лекция отменялась, я был рад. Почему? Не знаю, какая-то психология — я не мог и сейчас не могу объяснить механизм.
Этими лекторами были Пётр Сергеевич Новиков и Израиль Моисеевич Гельфанд. Оба читали на мехмате, в старом здании на Моховой. У них были абсолютно противоположные стили.
У Новикова лекция часто состояла из поправок к предыдущей: он исправлял неточности, даже ошибки. Общение со студентами было, я бы сказал, повышенно любезное. Студентов было мало — это были необязательные лекции по дескриптивной теории множеств, факультатив для желающих. Сидело человек 12, а то и меньше. Помню неприятный момент, когда пришла сотрудница деканата и переписала, кто с мехмата, — оказалось трое.
Народу было так мало, что однажды, когда я не мог прийти на следующую лекцию, я его предупредил — было бы заметно. Его реакция была совершенно неожиданной, он сказал: «Ну, так мы отменим». Я его предупредил перед лекцией, и он начал ее с объявления, что следующая лекция будет не по расписанию, а через раз.
Среди постоянных слушателей был Есенин-Вольпин. Вот Новиков говорит: «А теперь мы должны ввести целое множество символов». Есенин-Вольпин, естественно, спрашивает: «А что такое символ?» («Википедия»: «Основу математических и философских взглядов Есенина-Вольпина составляет крайний скептицизм — отрицание всех принимаемых на веру абстрактных понятий». — М.Г.). И вся лекция уходит на выяснение того, что такое символ. При этом всё у меня было записано, мои конспекты даже ездили в Воронеж ценной бандеролью. Дескриптивная теория множеств — это вещь тяжелая.
Теперь Гельфанд. Продумано всё до последней мелочи. Необычайно изящно. Он когда-то сказал: «Моцарт! Он не делает ошибок!» (Это было про Колмогорова, который под конец жизни как раз допустил пару ошибок и очень расстраивался.) И вот он сам изяществом стиля своих лекций был, как Моцарт. Это был 1950/1951 учебный год, обязательные лекции по интегральным уравнениям для четвертого курса. Они читались в одной из больших, но плоских аудиторий (самые большие аудитории — амфитеатром).
Лекции обязательные для четвертого курса, но на них приходят с других курсов, с других факультетов (с физического бегают) — сидят на подоконниках, висят на люстрах. Читает очень ясно, но как-то раз я чего-то не понял. Я послал ему записку, что такое-то место мне непонятно; не подписался. Он прочитал записку и сказал: «Ну, только полный идиот может написать такое. Он ничего не понимает с самого начала, и не понятно, что он вообще тут делает». Высказался по полной программе. Я пришел в бешенство: «Твою мать — я студент, ты профессор, я могу чего-то не понять, твое дело объяснить — ну или сказать, что сейчас не время, и объяснить после лекции — но не хамить».
А еще у него была манера тыкать пальцем в произвольного студента и вызывать к доске. И он тыкает в меня, совершенно случайно: «Вот, мы дошли до такого места, что мы дальше должны делать?» Я знаю, но говорю: «Я не знаю». Он спрашивает: «Как это Вы не знаете?» И начинает на меня орать. Когда он кончил орать, я сказал: «Не знаю я потому, что я забыл дома очки и не вижу». Я действительно забыл очки, но, напрягшись, со второго ряда мог разглядеть, хотя с трудом, и всё понял и записал. Он говорит: «Чего Вы тогда тут сидите?» И вот тут я ему врезал. Я сказал: «Сижу я тут потому, что у нас обязательное посещение». Еще раз повторяю: сидят на подоконниках, с других курсов, с других факультетов, и вообще, это огромное событие — лекции Гельфанда. Что он мог сказать? — «Садитесь».
Я понимаю, что накликал беду на свою голову. Потом экзамен. Экзамен у Гельфанда происходит так: он запускает сразу человек двадцать. Всем дает задачу, каждому свою, а сам бегает и смотрит. Решил человек задачу — может выбрать: немедленно получить тройку или, если хочет больше, ему опять дается задача, уже следующего уровня, и всё повторяется.
Мне он дает задачу, русским языком сказать, охренительную. Я чрезвычайно себя ругаю, что ее не записал. Несколько лет помнил, потом забылось.
Решить я ее не могу. Он на меня поглядывает с большим удовлетворением — конечно, он меня запомнил. Так проходит два часа. Экзамен еще продолжается, кто-то приходит, уходит. Он видит, что у меня ничего нет. Подходит и спрашивает: «Ну, как у Вас?» Я говорю: «Вот у меня такие-то соображения». Он опять начал орать: «Меня не интересуют Ваши соображения! Меня интересует, решили Вы задачу или не решили. Если решили — пишите решение. Если не решили — так и скажите: «Не решил»».
Дальше произошло нечто невероятное. У меня было такое впечатление, что от этого крика у меня в мозге разорвалась какая-то пленка. Даже как будто звук раздался. И в эту самую минуту задача решилась. Конечно, всё это время, пока я сидел, что-то такое у меня в селезенке и родственных органах происходило. Но вот от крика всё решилось. И я тогда ему ехиднейшим голосом говорю: «Простите, Израиль Моисеевич, я думал, Вас интересуют мои соображения, но если Вас интересует всего лишь решение, вот оно». И выписываю ему решение. Мы оба обалдели совершенно одинаково. Он же видел, что у меня нет ничего... Но надо отдать ему должное, он не стал мне давать другой задачи: эта задача уже была на «шесть». Он с отвращением поставил мне «пять», и я удалился.
А дальше происходит следующее. Подходит конец моей аспирантуры. Она заканчивается 15 ноября 1955 года. Наступает весна 55-го года, а диссертация у меня не написана. Она у меня вся есть в голове, есть публикации — надо сесть и записать. И тут моя жена принимает чрезвычайно странное решение — чтобы я написал диссертацию, меня надо послать в курортный город Палангу, в пансионат Союза писателей. Почему он назывался «пансионат», не ясно — там давали только кров, никакого пансиона не было, питайся, где хочешь.
У меня была комната под крышей, которая страшно раскалялась. Мне было скучно писать диссертацию, поэтому я сначала отредактировал перевод Есенина-Вольпина книги Клини «Введение в метаматематику». Есенин-Вольпин, переведя Клини, совершил этим, конечно, подвиг, но переводил он так. Вот такая фраза: «Все f E g» — как ее надо понять?.. В оригинале было: «All f’s of E are g’s». По-английски «’s» — это множественное число. По-русски как писать — «f-ы»? «g» — это ранее введенные объекты. «Е», оказывается, стоит в родительном падеже. И еще тут пропущено сказуемое-связка. Потом я написал большую статью в «Успехи математических наук», а потом стал лихорадочно писать диссертацию, потом уже в Москве ее дописал, отдал перепечатать и успел защититься в срок.
Ну вот. Приезжаю я в этот пансионат, и первых, кого я вижу, — Гельфанда с семьей, Зорей Яковлевной и тремя сыновьями, старшему из которых, Сереже, было 11 лет; это был Ваш отец. И Гельфанд меня видит. Смешанные чувства отражаются на его лице. С одной стороны, он меня терпеть не может, как мы потом, на следующий день, выяснили. Как и я его. Но там писатели, причем половина — литовских, и я единственный, с кем можно разговаривать. Нет повода для сближения, но происходит вот что: отключается электричество. Там несколько щитов с переключателями, с пробками, что-то перегорело.
И он говорит так: «Вы бегайте по этажам и там выкручивайте и вкручивайте лампочки, а я буду стоять на первом этаже и по Вашим указаниям менять пробки на центральном щите. Это же по Вашей части» (тогда компьютеров не было, главным приложением логики были релейно-контактные схемы). Я начинаю бегать и понимаю, что произошло: я вычисляю ту лампочку, которая перегорела, и сгоревшую пробку; по одной никак не сходилось. Я тогда был молодой, и в голове что-то еще работало. Я ему указал пробку, он ее поменял, и всё заработало. И дальше мы уже довольно быстро подружились.
Он спросил, чем я занимаюсь, я ответил, и он сказал: «Ну, хорошо, читайте мне лекции по теории алгоритмов». Мы садились на скамеечке, и я ему прочел три лекции, даже рассказал одну свою теорему, такую, которую можно изложить на пальцах даже с доказательством: рассмотрим вычислимые функции, у которых множество значений бесконечно; совокупность их программ сама не может быть множеством значений вычислимой функции. Это довольно просто и красиво доказывается, но как-то до меня никто не сообразил, что такая теорема может быть. Я ему рассказал, ему понравилось.
А в конце третьей лекции я сказал, что больше лекций читать не буду. «Почему, что такое?» А вот почему: я обратил внимание, что к скамейке, где мы сидели, подошел трехлетний мальчик и начал что-то лепить из песка, и Гельфанд этим заинтересовался и одним ухом меня слушает, а сам обернулся туда и с увлечением строит куличики. «Вы меня перестали слушать, значит, уже хватит: никакого упрека, но произошел естественный конец».
Когда уже надо было уезжать, он мне сказал: «Вы сейчас заканчиваете аспирантуру, я Вас беру в свой отдел в отделении прикладной математики» (оно в несколько раз превосходило численностью, влиянием и финансами Математический институт Академии наук, отделением которого считалось) — «А что я там буду делать?» — «Мы с Вами будем писать книгу. Там надо будет охватить всю математику, но не просто общее введение, а в каждом разделе мы возьмем по яркой теореме. Вот я Вам сейчас расскажу, и мы обсудим». Ну, «обсудим» — это просто так сказано говорил он, а я, раскрыв рот, слушал. Теорема о том, как устроены какие-то поверхности третьего порядка, что-то такое. Теорема о каких-то функционалах. Теорема о том, как у дифференциальных уравнений решения закручиваются куда-то. «Берем эти разделы и пишем, будем обсуждать, Вы будете записывать».
Я пошел к А.Н. Колмогорову, он мой учитель (как, кстати, и Гельфанда). Я сказал, что меня пригласил Гельфанд, это большая честь. «Да, большая честь. Но я Вам скажу, что будет. В течение года, а если повезет, то двух, Вы будете его любимой игрушкой. Через два года он забудет о Вашем существовании». Как мне потом сказали некоторые ученики Гельфанда, которые его хорошо знали, так бы оно и произошло. Поэтому я предпочел не рисковать и пошел по пути, который предложил Колмогоров, — на мехмат МГУ.
Примечания (составлены М. Гельфандом)
1. Иван Матвеевич Виноградов — специалист по теории чисел, много лет был директором Математического института им. В. А. Стеклова, прославившись в этом качестве своим антисемитизмом.2. B. M. Harvey et al. Topographic representation of numerosity in the human parietal cortex // Science. 2013. V. 341. P. 1123–1126.3. Ю. И. Манин: «Не мы выбираем математику своей профессией, а она нас выбирает». Троицкий вариант — Наука № 13 от 30.09.2008.4. Диагональ квадрата несоизмерима (не выражается дробью с целочисленным числителем и знаменателем) с его стороной; это эквивалентно иррациональности квадратного корня из двух.5. В. А. Успенский, А.Л. Семенов. Теория алгоритмов: основные открытия и приложения. М.: Наука. 1987 — 288 с.6.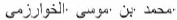 
— основатель классической алгебры. От его прозвища «аль-Хорезми» (хорезмиец) происходит слово «алгоритм».7. Three Olives, производится в Великобритании с 1998 года, но там не продается, а продается в США.8. Альберт Швейцер. Иоганн-Себастьян Бах. Пер.: М. Друскин. М.: Музыка, 1964 — 728 с.9. 
10. Тернарная проблема Гольдбаха: каждое число большее или равное шести является суммой трех простых чисел.11. Henri Leon Lebesgue — автор современной теории интегрирования (так называемый интеграл Лебега).12. Nicolas Lusin. Legons sur les Ensembles Analytiques et leurs Applications. Gauthier-Villars, 1930.-P. xvi+328. (См. также В. А. Успенский. Вклад Н.Н. Лузина в дескриптивную теорию множеств и функций: понятия, проблемы, предсказания // Успехи математических наук. 1985. Т. 40. Вып. 3 (243). С. 85–116.).13. А. Лебег. Предисловие к книге Н.Н. Лузина «Лекции об аналитических множествах и их приложениях» Пер. с французского В. В. Успенского // Успехи математических наук. 1985. Т. 40. Вып. 3 (243). С. 9–14.14. Михаил Яковлевич Суслин — автор (совместно с Н.Н. Лузиным) теории аналитических множеств (А-множеств).15. Факультет вычислительной математики и кибернетики МГУ.16. Ответ: «В аудитории найдется хотя бы один студент, который не знает ни баскского, ни чукотского языка».17. Например, решим две задачи. (1) В ящике лежат 2 черных носка и 2 серых. Из ящика (не глядя) вынимают носок и потом еще один. Какова вероятность, что носки составили пару одного цвета? Ответ: 1/3. (2) В ящике лежат 2 черных носка и 2 серых. Из ящика (не глядя) вынимают носок, кладут обратно и потом опять вынимают носок. Какова вероятность, что были вынуты носки одного цвета? Ответ: 1/2.18. В. А. Успенский. Математическое и гуманитарное: преодоление барьера. Изд. 2е. М.: МЦНМО, 2012 — 48 с.19. «Википедия». Статья «Лузин, Николай Николаевич».
elementy.ru
Математика возникла очень давно. Человек собирал фрукты, выкапывал плоды, ловил рыбу и запасал все это на зиму. Чтобы понять, сколько запасено пищи человек изобрел счет. Так начала зарождаться математика.
Затем человек стал заниматься земледелием. Надо было измерять участки земли, строить жилища, измерять время.
То есть человеку стало необходимо использовать количественное отношение реального мира. Определить сколько собрали урожая, каковы размеры участка под застройку или как велик участок неба, на котором определенное количество ярких звезд.
Кроме того, человек стал определять формы: солнце круглое, короб квадратный, озеро овальное, и как эти предметы располагаются в пространстве. То есть человек стал интересоваться пространственными формами реального мира.
Таким образом, понятие математика можно определить как науку о количественных отношениях и пространственных формах реального мира.
В настоящее время нет ни одной профессии, где бы можно было бы обойтись без математики. Известный немецкий математик Карл Фридрих Гаусс, которого назвали «королем математики» как-то сказал:
«Математика – царица наук, арифметика – царица математики».
Слово «арифметика» происходит от греческого слова «арифмос» – «число».
Таким образом, арифметика это раздел математики, изучающий числа и действия над ними.
В начальной школе, прежде всего, изучают арифметику.
Как же развивалась эта наука, давайте, исследуем этот вопрос.
Основным периодом накопления математических знаний считается время до V века до нашей эры.
Первым, кто стал доказывать математические положения – древнегреческий мыслитель Фалес Милетский, живший в VII веке до нашей эры предположительно 625 – 545 года. Этот философ путешествовал по странам востока. Предания говорят, что он учился у египетских жрецов и вавилонских халдеев.
Фалес Милетский принес из Египта в Грецию первые понятия элементарной геометрии: что такое диаметр, чем определяется треугольник и так далее. Он предсказал солнечное затмение, проектировал инженерные сооружения.
В этот период постепенно складывается арифметика, развивается астрономия, геометрия. Зарождается алгебра и тригонометрия.
Это период начинается с VI до нашей эры. Теперь математика возникает как наука с теориями и доказательствами. Появляется теория чисел, учение о величинах, об их измерении.
Наиболее известным математиком этого времени является Евклид. Он жил в III веке до нашей эры. Этот человек является автором первого из дошедших до нас теоретического трактата по математике.
В трудах Евклида даны основы, так называемой евклидовой геометрии – это аксиомы, упирающиеся на основные понятия, такие как точка, прямая, плоскость и их отношение.
В период элементарной математики зарождается теория чисел, а также учение о величинах и их измерении. Впервые появляются отрицательные и иррациональные числа.
В конце этого периода наблюдается создание алгебры, как буквенного исчисления. Сама наука «алгебра» появляется у арабов, как наука о решении уравнений. Слово «алгебра» в переводе с арабского означает «восстановление», то есть перенос отрицательных значений в другую часть уравнения.
Основоположником этого периода считается Рене Декарт, живший в XVII веке нашей эры. В своих трудах Декарт впервые вводит понятие переменной величины.
Благодаря этому ученые переходят от изучения постоянных величин к изучению зависимостей между переменными величинами и к математическому описанию движения.
Наиболее ярко этот период охарактеризовал Фридрих Энгельс, в своих трудах он писал:
«Поворотным пунктом в математике была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика, и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление, которое тотчас и возникает, и, которое было в общем и целом завершено, а не изобретено Ньютоном и Лейбницем».
В 20 годах XIX века Николай Иванович Лобачевский становится основоположником, так называемой неевклидовой геометрии.
С этого момента начинается развитие важнейших разделов современной математики. Такие как теория вероятности, теория множеств, математическая статистика и так далее.
Все эти открытия и исследования находят обширное применение в самых разных областях науки.
И в настоящее время наука математика бурно развивается, расширятся предмет математики, включая новые формы и соотношения, доказываются новые теоремы, углубляются основные понятия.
Спасибо, что Вы с нами!
Понравилась статья - поделитесь с друзьями:
Подпишитесь на новости сайта:
Оставляйте пожалуйста комментарии в форме ниже
beginnerschool.ru
Это древнегреческое слово является однокоренным с глаголом μανθάνω (manthanō) - учиться, изучать, понимать. А существительное ὁ μαθητής (mathētēs), встречающееся и в Новом Завете, обозначает вовсе не математика, а ученика или последователя какого-то учителя или учения.
В связи с такой любопытной этимологией я хотел бы отметить две очень важные, как мне кажется, вещи.
1) Во-первых, конечно, есть четкая логика в том, что слово, значившее сначала науку или знание вообще, потом закрепилось за наукой математикой. Ведь математика очень долго считалась образцом строгости и научности для всех других наук, своего рода королевой в царстве знаний. Например, «Начала» древнегреческого математика Евклида больше двух тысячелетий служили образцом для любого научного труда, а классическая евклидова геометрия считалась единственно возможной геометрией.
Галилео Галилей, заложивший основы математической физики, говорил, что книга природы написана на языке математики, и что надо уметь ее читать. Философ Спиноза строил свою знаменитую «Этику» more geometrico, т.е., по евклидову образцу - с аксиомами, теоремами, их доказательствами и леммами. А Карл Маркс однажды сказал даже, что любая наука лишь тогда станет совершенной, когда ей удастся воспользоваться математикой.
Современную физику нельзя представить нематематической. Знаменитый физик, лауреат Нобелевской премии по физике 1979 года Стивен Вайнберг говорит, что суть современной физики - по-прежнему количественное понимание явлений. И даже в квантовой физике то, что «материя исчезла», что стало совершенно непонятно, что же такое атом и его составные части (волны это или частицы), что они совершенно непредставимы и неизобразимы, эту неуловимость вещества поставили под численный учет и контроль (принцип неопределенности Гейзенберга). Современная неклассическая физика все равно измеряет неизмеримое, потому что она в принципе не может перестать считать, измерять и смотреть на мир через призму количественных отношений.
Однако где-то со второй половины XIX века все более и более ясным становилось то, что и математика тоже не является безусловным и строгим знанием, что ее основания тоже проблематичны. Кроме евклидовой геометрии были открыты геометрии неевклидовы - геометрии Лобачевского и Римана. С открытием теории относительности даже обнаружилось, что неевклидова геометрия согласно ей более адекватно описывает свойства космоса, мира в целом.
К началу ХХ века в математике также обнаружился кризис ее оснований, как и в других науках. Например, были обнаружены логико-математические парадоксы, которые сделали явной невыполнимость такой программы исследований оснований математики, которая получила название логицизма, то есть сведения всех математических положений к основоположениям логики. Поэтому доказать, что математика является логически непротиворечивой системой, не удалось. Самым знаменитым логико-математическим парадоксом, не имеющим решения, является парадокс Рассела. В более легкой формулировке он известен как парадокс брадобрея:
Единственному деревенскому брадобрею приказали: «Брить всякого, кто сам не бреется, и не брить того, кто сам бреется». Кто побреет брадобрея, и как ему поступить с сами собой? Брить или нет?
Словом, математика разделила судьбу всех других наук - от веры в их незыблемость и истинность до осознания их проблематичности и ненадежности самых главных основ. В ней произошло то, что можно назвать утратой определенности. Именно так - «Математика: утрата определенности» - называется блестящая научно-популярная книга о трудном историческом пути математики как науки известного американского математика Мориса Клайна.
Как он писал в «Введении», «эта книга - горестный рассказ о бедствиях, выпавших на долю математики - наиболее древнего и не имеющего себе равных творения людей, плода их неустанных и многообразных усилий, направленных на использование способности человека мыслить. Можно также сказать, что эта книга на общедоступном уровне повествует о расцвете и закате величия математики...
В настоящий момент положение дел в математике можно обрисовать примерно так. Существует не одна, а много математик, и каждая из них по ряду причин не удовлетворяет математиков, принадлежащих к другим школам. Стало ясно, что представление о своде общепринятых, незыблемых истин - величественной математике начала XIX в., гордости человека - не более чем заблуждение. На смену уверенности и благодушию, царившим в прошлом, пришли неуверенность и сомнения в будущем математики. Разногласия по поводу оснований самой "незыблемой" из наук вызвали удивление и разочарование (чтобы не сказать больше). Нынешнее состояние математики - не более чем жалкая пародия на математику прошлого с ее глубоко укоренившейся и широко известной репутацией безупречного идеала истинности и логического совершенства».
2) Второе обстоятельство, связанное с математикой, имеет отношение к тому, что христианская вера - это именно вера, к ней неприложимы рациональные критерии, действующие в научном знании.
Ведь самые основы христианства - учение о Боге-Троице - вступают в полное противоречие с самыми элементарными математическими положениями. Ибо как можно рационально понять и осмыслить то, что Бог един и одновременно троичен?
Что Он - един в Трех Лицах? Что Святая Троица - Бог-Отец, Бог-Сын и Бог-Дух Святой - это три Лица Единственного и Единого Бога? Что три здесь равно одному, единице? Это входит в полное противоречие с нашими элементарными умственными и математическими навыками и привычками, с правилами счета, которые любой человек осваивает, как правило, еще в дошкольном возрасте.
Кстати, интересно и показательно, что великий английский физик Исаак Ньютон, основоположник математизированной классической физики в молодости учился в Кембриджском университете в колледже Святой Троицы и даже подумывал стать священником, но в итоге решил не связывать свою судьбу со священническим служением именно из-за сомнений в учении о Троице. Да и позже он активно высказывал свои антитринитарские воззрения.
Так что, наверно, прав был Тертуллиан, автор знаменитого «Верую, ибо абсурдно», и не менее знаменитого риторического вопроса «Что общего между Афинами и Иерусалимом?» В данном случае он просто выразил то, как следует грамотно думать о христианской вере, то, что она не знание, а именно вера, которая в своей основе радикально противоречит нашему логическому и математическому рацио, рассудку. Верить можно только в то, что не можешь знать сам по себе.
ПУЩАЕВ Юрийhttp://foma.ru/matematika-nauka.html
ruskline.ru
математика - наука о количественных зависимостях.
арифметика - изучает свойства целых и рациональных чисел.
теория чисел.
геометрия.
планиметрия. стереометрия. топология. начертательная геометрия.
неэвклидова геометрия. гиперболическая геометрия. тригонометрия.
теория вероятностей. математическая статистика.
дискретная математика.
теория игр. исследование операций. теория множеств. теория графов.
теория алгоритмов. теория кодирования. теория цифровых автоматов.
вычислительная математика.
Идеографический словарь русского языка. — М.: Издательство ЭТС. Баранов О.С.. 1995.
Математическая биология — это теория математических моделей биологических процессов и явлений. Математическая биология может быть отнесена к прикладной математике и активно использует её методы. Критерием истины в ней является математическое доказательство. Важнейшую роль … Википедия
НАУКА — особый вид познавательной деятельности, направленный на выработку объективных, системно организованных и обоснованных знаний о мире. Взаимодействует с др. видами познавательной деятельности: обыденным, художественным, религиозным, мифологическим … Философская энциклопедия
МАТЕМАТИЧЕСКАЯ ГЕОГРАФИЯ — (греч.). Часть землеописания, имеющая своим предметом положение земли относительно других небесных тел. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МАТЕМАТИЧЕСКАЯ ГЕОГРАФИЯ греч. Наука о положении земли… … Словарь иностранных слов русского языка
Наука и гипотеза — «НАУКА И ГИПОТЕЗА» книга выдающегося франц. математика, физика и философа Анри Пуанкаре, вышедшая в 1902 г., в рус. пер. вошла в состав его книги «О науке» (М., 1983). Основное содержание «Н. и г.» составляют е г о доклады на… … Энциклопедия эпистемологии и философии науки
Математическая статистика — [mathematical statistics] раздел математики, посвященный методам и правилам обработки и анализа статистических данных (т.е. сведений о числе объектов, обладающих определенными признаками, в какой либо более или менее обширной совокупности). Сами… … Экономико-математический словарь
математическая статистика — Раздел математики, посвященный методам и правилам обработки и анализа статистических данных (т.е. сведений о числе объектов, обладающих определенными признаками, в какой либо более или менее обширной совокупности). Сами методы и правила строятся… … Справочник технического переводчика
наука — НАУКА особый вид познавательной деятельности, нацеленный на выработку объективных, системно организованных и обоснованных знаний о мире. Социальный институт, обеспечивающий функционирование научной познавательной деятельности. Как … Энциклопедия эпистемологии и философии науки
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Истоки математической статистики можно найти в сочинениях ученых конца 17 начала 19 вв. Во многих… … Современная энциклопедия
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность … Большой Энциклопедический словарь
Математическая статистика — МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Истоки математической статистики можно найти в сочинениях ученых конца 17 начала 19 вв. Во многих… … Иллюстрированный энциклопедический словарь
ideographic.academic.ru
|
|
|
|
|
|
