Скачать эту презентацию
Скачать эту презентацию
№ слайда 1
Описание слайда: Математика в ребусах Выполнила: Сергеева Анна 5 а класс Учитель: Таренко Е.А.
№ слайда 2
Описание слайда: Введение Я выбрала эту тему, потому что сама очень люблю разгадывать ребусы. Ребусы всегда подаются в увлекательной форме, они прогоняют интеллектуальную лень, вырабатывают привычку к умственному труду, воспитывают настойчивость в преодолении трудностей. В отличие от простой загадки, где основа идет на словесное описание, ребус развивает еще и логическое образное мышление, учит ребенка нестандартно воспринимать графическое изображение, а также тренирует зрительную память и правописание.В процессе выполнения этой работы мы узнаем:когда и где появились первые ребусы,какими бывают ребусы,научимся разгадывать ребусы,я придумаю и нарисую свои ребусы,- составлю кроссворд с помощью ребусов
Описание слайда: Из история ребусовРебус – это загадка изображенная рисунками, знаками, буквами и другими фигурами, ответ на которую получается путём сопоставления составных его частей по расположению, форме, виду. В основном ребусы - это детские загадки. Детям ребусы разгадывать очень интересно, так как это в основном они составлены из картинок. Более сложным видом являются математические ребусы - загадка, представляющая собой математическое вычисление. Название образовано
№ слайда 4
Описание слайда: Из история ребусовПервые ребусы появились во Франции в XV веке. Со временем характер ребуса изменился. Ребусом стали называть каламбур, построенный на игре слов. Приблизительно тогда же появились и первые рисованные ребусы. В XVI веке рисованные ребусы становятся известны в Англии, Германии, Италии. В их оформлении принимали участие профессиональные художники. Первый печатный сборник ребусов появился во Франции в 1582 году. В России ребусы появились позднее - в середине XIX века. Сначала они появляются в журнале "Иллюстрация", а в 1880 году начинает издаваться журнал "Ребус". Им увлекались многие взрослые и дети, и разгадывание ребусов вскоре стало одной из любимых семейных игр.
Описание слайда: Какими бывают ребусыКлассический ребусКлассический ребус — это головоломка, в которой необходимо разгадать зашифровывание с помощью рисунков, букв и знаков — слова и фразы.Арифметический ребусСуществует разновидность ребусов, называемых арифметическими. Эти ребусы представляют собой примеры обычных арифметических действий (вычитания, сложения, деления и умножения), в которых часть или даже все цифры заменены на точки, звездочки, буквы или другие символы. каждый символ может обозначать любую цифру от 0 до 9. В таких ребусах некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе. Решить ребус - восстановить первоначальный вид примера.
№ слайда 6
Как разгадывать ребусыОзнакомившись с правилами как разгадывать ребусы, вы сможете без особого труда не только справиться с любым ребусом, но и узнаете как составить ребус самому.1) Название всего, что изображено на картинках в ребусе, читается только в именительном падеже.2) Картинка в ребусе может иметь не одно название. Пример: нога и лапа, глаз и око; или изображение может иметь общее или частное название (птица - общее название; петух, голубь, чайка - частное название).3) Запятые (не имеет значения, перевёрнутые или нет) указывают, что из слова следует убрать крайние буквы. Сначала слова, если запятые стоят перед картинкой, или с конца слова, если запятые после картинки. Количество букв, которые нужно убрать, соответствует количеству запятых. ЛЕС
№ слайда 7
Описание слайда: Как разгадывать ребусы4) Зачёркнутые буквы - такие буквы следует убрать из слова. Если зачёркнутые буквы повторяются, то они убираются все. КАССА5) Зачёркнутые цифры указывают, что в слове такую по счёту букву надо убрать.6) Знак равенства между буквами (А=Е) указывает, что нужно заменить все буквы А на Е. Равенство 1=Е указывает на замену только первой буквы в слове.7) Стрелка между буквами (Е -> В) тоже указывает на соответствующую замену букв.8) Цифры 1,2,7,5 над картинкой указывают, что из данного слова нужно взять буквы под номерами 1,2,7,5 и составить их в том порядке, в котором расположены цифры.
Описание слайда: Как разгадывать ребусы9) Перевёрнутый вверх ногами рисунок указывает, что слово следует читать справа налево. (КОТ - ТОК)10) Стрелка, остриём влево, изображённая над картинкой указывает, что после того как слово разшифровано его нужно прочитать задом наперёд. КОТ11) Когда в ребусе используется дробь, это разгадывается как "НА" (разделить НА). Если же в ребусе используется дробь со знаменателем 2, то это разгадывается как "ПОЛ" (половина).
№ слайда 9
Описание слайда: Как разгадывать ребусы13) Внутри буквы "О" расположен слог "ДА", получается В-О-ДА, т.е. "ВОДА". Также это можно прочитать как "ДА-В-О". Выбирается вариант, подходящий по смыслу. ВОЛЯ14) Когда картинки расположены друг над другом, это читается как "НАД", "НА", "ПОД" (в зависимости от того, что подходит по смыслу).15) Буква, состоящая из других букв, читается как предлог "ИЗ". Например из буквы "Б" составим букву "А", то получим: из «Б» «А» (ИЗБА).
Описание слайда: Как разгадывать ребусы16) Буква, расположенная поверх другой буквы, читается как "ПО". ПОЛЕ17) Буква, изображённая за другой буквой, читается как предлог "ЗА" или «ПЕРЕД». Выбирается вариант, подходящий по смыслу. ЗАЯЦ18) Знак "+" означает предлог "К" (Прим. 2+3 можно прочитать: К Двум прибавить Три или Три прибавить К Двум). Следует выбирать вариант подходящий по смыслу.
№ слайда 11
Описание слайда: Как разгадывать ребусы19) Двойная стрелка между цифрами означает, что буквы под этими номерами нужно поменять местами друг с другом. 20) Перечёркнутый знак "=" между картинками следует читать как "НЕ" (Прим.: «С» НЕ равно «Г»). Лапка
№ слайда 12
Классический ребус
№ слайда 13
Описание слайда: ОТРЕЗОК
№ слайда 14
Описание слайда: Классический ребус
№ слайда 15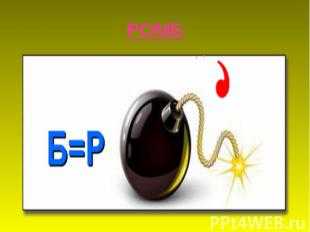
Описание слайда: РОМБ
№ слайда 16
Описание слайда: Классический ребус
№ слайда 17
Описание слайда: Дробь
№ слайда 18
Описание слайда: Классический ребус
№ слайда 19
Описание слайда: Знаменатель
№ слайда 20
Описание слайда: Классический ребус
№ слайда 21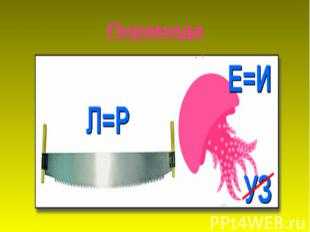
Описание слайда: 
Описание слайда: Классический ребус
№ слайда 23
Описание слайда: Задача
№ слайда 24
Описание слайда: Какое число должно стоять вместо «?»?
№ слайда 25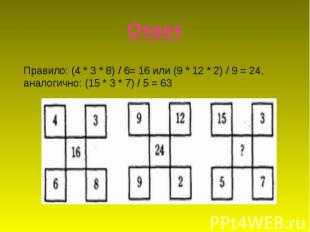
Описание слайда: ОтветПравило: (4 * 3 * 8) / 6= 16 или (9 * 12 * 2) / 9 = 24, аналогично: (15 * 3 * 7) / 5 = 63
№ слайда 26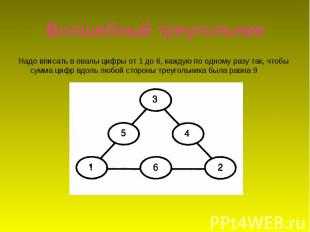
Описание слайда: Волшебный треугольникНадо вписать в овалы цифры от 1 до 6, каждую по одному разу так, чтобы сумма цифр вдоль любой стороны треугольника была равна 9
№ слайда 27
Описание слайда: Арифметический ребусК Р О С С + К Р О С С = С П О Р Т Ответ35977 + 35977 = 71954
№ слайда 28
Описание слайда: 
Описание слайда: Арифметический ребус С Л О В О + С Л О В О = П Е С Н Я ответ 14565 + 14565 = 29130
№ слайда 30
Описание слайда: Кроссворд 2 3 5 6 8 910
№ слайда 31
Описание слайда: ВыводВыполнив эту работу я узнала какие бывают ребусы, как их разгадывать, где и когда появились первые из них. Важно и то, что я сама придумала ребусы и кроссворд с их применением. В творческой работе специально был подобран интересный материал, который не встречается в школьном курсе, а если и встречается, то менее ярко преподносится. В эту работу было внесено много примеров и задач, которые помогают лучше понять данный материал. Думаю, данная работа может послужить методическим пособием для проведения краткого факультатива, а так же использоваться на уроках математики в школе.
Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.
Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до н.э.). Задач в сборнике много — ниже одна из них.
Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем одну из них — настолько «бородатую», что ее знают школьники во всем мире.
Как крестьянину перевезти все в целости и сохранности?
На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.
Попробуйте сосчитать, сколько равносторонних треугольников изображено на печати.
Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.
«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».
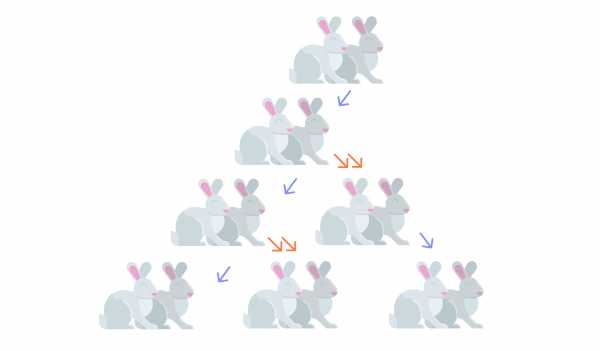
Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?
Смотреть подсказку и ответВспомните последовательность Фибоначчи или запаситесь терпением — и считайте.
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, …, …).
Ответ: 233 пары.
Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.
Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.
Как выполнить завещание?
Показать решениеСам Тарталья предложил следующее решение. Для раздела имеющихся лошадей необходимо заимствовать еще одну, после чего их общее количество станет 18. Раздел этого количества даст 2, 6 и 9 лошадей, которых в сумме окажется 17. Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть владельцу после раздела имущества.
Можно решить головоломку и арифметическим способом: пропорцию 1/2 : 1/3 : 1/9 достаточно умножить на 18 и получится тот же результат.
Ответ: 2, 6 и 9 лошадей.
Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику. Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:
Нарисуйте фигуру, изображенную на рисунке.
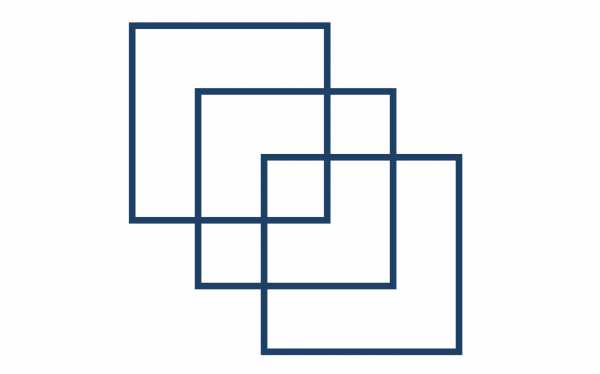
Задача усложняется особыми условиями ее выполнения:
Ниже мы изобразили 2 варианта решения. Возможно, вам удастся найти и другие.
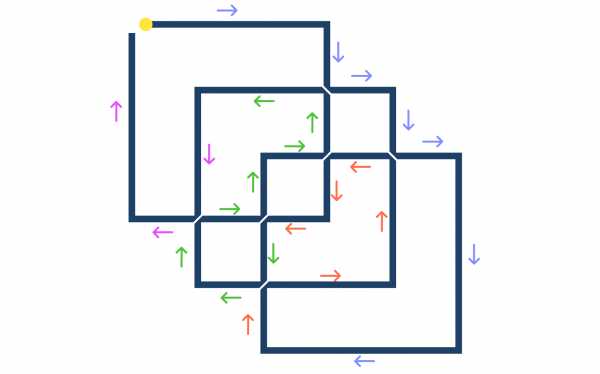
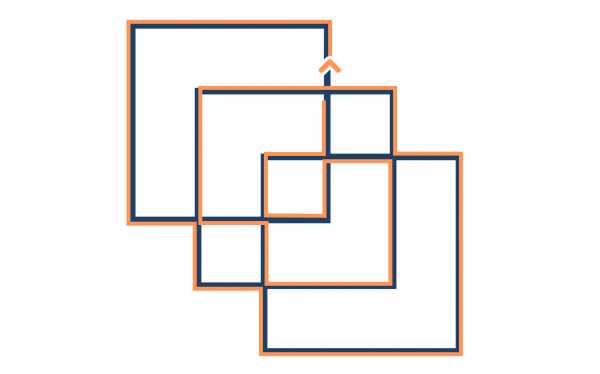
Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.
Предлагаем решить одну из самых популярных головоломок Гарднера.
Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.
Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.
Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.
Шерил показала поклонникам 10 возможных дат:
Затем она показала Альфреду месяц своего рождения, а Бернарду — день.
Чтобы решить головоломку, друзья обменялись парой реплик:
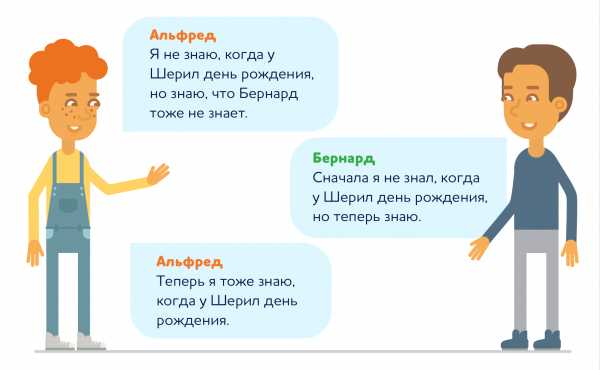
Так когда же у Шерил день рождения?
Смотреть решение и ответДаты находятся в промежутке от 14 до 19. Числа 18 и 19 встречаются по разу. Если день рождения в эти даты, то Бернард сразу бы сказал месяц.
Если Шерил сказала Альфреду, что родилась в мае или июне, значит, день рождения может быть 19 мая или 18 июня. Раз Альфред точно знает, что Бернард не знает ответ, значит, речь не о мае или июне. Остаются июль или август.
В июле и августе остались даты в диапазоне от 15 до 17, а 14 встречается дважды. Если бы день рождения был 14-го, то Бернард после реплики Альфреда еще не мог бы дать точного ответа. Значит, речь не о 14-ом. Остаются 16 июля, 15 августа и 17 августа.
Если бы Шерил сказала Альфреду, что родилась в августе, то после ответа Бернарда, Альфред не мог бы точно узнать дату рождения — ведь целых 2 даты приходятся на август.
Значит, Шерил родилась 16 июля.
Ответ: 16 июля.
Эту задачку Конгу показала племянница друга. Она же разыграла телеведущего, сказав, что головоломка предназначена для 10-летних школьников. Дебаты о том, как решить «простую» задачку, развернулись нешуточные. Спустя 2 дня, когда большинство участников сдались, выяснилось, что задача — олимпиадная, для 14-летних школьников.
Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.
Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей: 5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.
Суть «свободной» игры в танграм - собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ. Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.
Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.
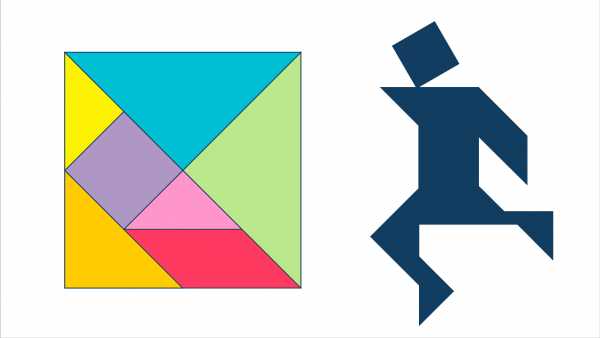
Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.
Помните 2 правила головоломки: 1) необходимо использовать все 7 фигурок головоломки; 2) фигуры не должны накладываться друг на друга.
Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд. В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.
Со всеми головоломками успешно справились? Великие математики и логики мира гордились бы вами!
Делитесь ссылкой с друзьями — пусть и они проверят свои силы!
На ЛогикЛайк вас ждут более 2500 заданий на развитие логического, математического и пространственного мышления.
logiclike.com
Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-278579
Похожие материалы
Оставьте свой комментарийinfourok.ru
|
|
|
|
|
|
