"Математические ребусы" разработка может быть использована при проведении различных игр или соревнований, для детей 4-6 классов. Содержит теоретический материал,а именно, основные правила, руководствуясь которыми, разгадываются ребусы и практические задания для соревнования.
Математические ребусы
Конкурс для проведения недели математики для 5-7 классов
МАОУ СОШ№2им.ТрубилинаИ.Т.
Учитель математики Колган М.А
Ребус - вид загадки, в которой разгадываемые слова даны в виде рисунков в сочетании с буквами или цифрами.
Правила разгадывания ребусов:
1. Запятая слева от слова означает количество букв, которые нужно удалить с начала слова.
Было "ШПРИЦ" стало " ПРИЦ".
2. Перевернутая запятая справа означает количество букв, которые нужно удалить с конца слова.
Было " ПАЛЬМА " стало " ПАЛЬ ".
3. Если над словом перечеркнутые буквы, то это означает, что их нужно вычеркнуть. Если в слове несколько таких букв, то все они вычеркиваются.
Было "СТОЛ" стало "СТ".
4. Для замены букв внутри используют равенство типа И=Е, которое означает, что следует заменить все буквы И на Е. Если указано равенство типа 2=Р, то следует вторую букву заменить на Р.
Было "САЧОК" стало "САКОК".
5. Строчка вида 2,4,6,7 означает, что из слова необходимо использовать только буквы под номерами 2,4,6 и 7.
Было "БУДИЛЬНИК" стало "ИДУ".
6. Перевернутая картинка означает, что слово нужно читать справа-налево.
Было "КРОТ" стало "ТОРК".
7. При шифровании часто используют структуру начертания изображения.
Буква "Х" содержатся в букве "О", получаем х-в-о, т.е. "ХВО". Может быть обратный вариант в-о-х, т.е. "ВОХ". В зависимости от смысла выбирается один или другой.
Ребус №1
Ребус №2
Ребус №3
Ребус №4
Ребус №5
Ребус №6
Ребус №7
Ребус №8
Ребус №9
Ребус №10
ОТВЕТЫ:
Ребус 1
Ребус 2
ЗАДАЧА
Ребус 3
ТОЧКА
Ребус 6
Ребус 4
Ребус 7
МИНУС
УГОЛ
Ребус 5
ОТРЕЗОК
ЛИНЕЙКА
Ребус 8
Ребус 9
ПОДВАЛ
ТРАНСПОРТИР
Ребус 10
ЧИСЛО
АЛГЕБРА
multiurok.ru
Криптарифм. Математические буквенные ребусы
Криптарифм (cryptarithm) - это математический ребус, в котором зашифрован пример на выполнение одного из арифметических действий. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Считается, что никакое число не должно начинаться с нуля.
Криптарифм можно считать хорошим, если в результате шифрования получилась какая-то осмысленная фраза. Например, классическим криптарифмом является пример на сложение, придуманный Генри Э. Дьюдени еще в начале нашего века: SEND+MORE=MONEY. Кроме того, еще одно требование к правильному криптарифму: он должен иметь единственную возможную расшифровку.
Математические ребусы - прекрасная зарядка для ума. Вот лишь некоторые основные правила решения этих увлекательных математических загадок:
В буквенных ребусах каждой буквой зашифрована одна определенная цифра: одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы.
В ребусах зашифрованных, например, звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе.
Перед началом решения математического буквенного ребуса (например, криптарифма), убедитесь, что в нём использовано не более 10 различных букв. В противном случае, такой ребус не будет иметь решений.
Начните решение ребуса с правила, согласно которому ноль не может быть крайней левой цифрой в числе. Таким образом, все буквы и знаки, с которых начинается число в ребусе, уже не могут обозначать ноль. Круг поиска нужных цифр сузится.
В ходе решения отталкивайтесь от основных математических правил. Например, умножение на ноль всегда дает ноль, а при умножении любого числа на единицу, мы получим в результате исходное число.
Очень часто математические ребусы представляют собой примеры сложения двух чисел. Если при сложении сумма имеет больше знаков нежели слагаемые, значит сумма начинается с "1"
Обращайте внимание на последовательность арифметических действий. Если числовой ребус состоит из нескольких рядов знаков, он может решаться как по вертикали, так и по горизонтали.
Не бойтесь совершать ошибки. Возможно, они подскажут вам верный ход решения. Не пренебрегайте методом перебора. Некоторые ребусы потребуют длительного поэтапного решения, но в итоге вы будете вознаграждены верным ответом и отличной разминкой для вашей сообразительности.
Попробуем решить простой криптарифм.
Задача 1. АВССумма в последней строке зашифрована буквами. А обозначает одну из цифр от 1 до 9, В — другую цифру и С — третью. Необходимо определить каждую из этих цифр.
А А В ВС В В
Чтобы получить ответ, для начала найдем самый очевидный ключ к значению одной из букв. В данном случае таким ключом является значение крайней левой буквы С. Откуда могла появиться эта буква-цифра? Поскольку непосредственно над ней никаких символов нет, она получена в результате сложения А и В. А поскольку А и В не могут быть больше 8 и 9, То их сумма не может превышать 17 или 18, если добавится единица от сложения в правой колонке. Получается, что С - 1.
infourok.ru
Математические ребусы , кроссворды , кросснамберыИспользованы материалы книг: Ященко И. В. "Приглашение на математический праздник". - М.: МЦНМО, ЧеРо, 1998; Мантуленко В. Г., Гетманенко О. Г. "Кроссворды для школьников. Математика". - Ярославль: "Академия развития", 1998; Бизам Д., Герцег Я. "Многоцветная логика. 175 логических задач". - М.: "Мир", 1978.Задания 1 - 4. Решите числовые ребусы, где одинаковым буквам соот-ветствуют одинаковые цифры, а разным - разные. Задание 5. Угадав все слова и записав их в клеточки по горизонтали, в выделенном вертикальном столбце вы прочтете фамилию известного ученого-математика Древней Греции. 1. Отрезок прямой, образующий прямой угол с данной прямой и имеющий одним из своих концов их точку пересечения, есть ... к данной прямой. 2. Элемент прямоугольного треугольника. 3. Треугольник есть геометрическая ... . 4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны. 5. Два луча, исходящие из одной точки. 6. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 7. Замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки O. Задание 6. По горизонтали:3. Отрезок прямой, соединяющий точку окружности с ее центром. 6. Утверждение, не требующее доказательства. 9. Конструкция, система мысли. 10. Вид четырехугольника. 15. Отрезок прямой, соединяющий две точки кривой. 16. Мера длины. 17. Тригонометрическая функция. 18. Точка пересечения диаметров окружности. 19. Тригонометрическая функция. 20. Часть окружности. 21. Старинная мера длины.По вертикали:1. Символ какого-либо алфавита. 2. Вид параллелограмма. 4. Хорда, проходящая через центр окружности. 5. Геометрический элемент. 7. Луч, делящий угол пополам. 8. Символ греческого алфавита. 10. Сумма длин сторон треугольника. 11. Вспомогательное предложение, используемое для доказательства. 12. Элемент прямоугольного треугольника. 13. Одна из замечательных линий треугольника. 14. Тригонометрическая функция.
|
trig.zodorov.ru
Теперь рассмотрим среднюю колонку. От сложения А и В помучилось то же В плюс единица «в уме». Чтобы это получилось, А должна иметь приличную величину, вероятно, 9. Поскольку при сложении этой цифры с той же единицей «в уме» из крайней правой колонки получится 10, при сложении которой с В внизу получится снова В. Значит, А = 9.
Наконец посмотрим на правую колонку. А и В дают С, которая, как уже известно, равна 1. Отсюда получается, что В=2. Итак, А = 9, В = 2 и С = 1.
Обратите внимание, как последовательно накапливается информация по ходу решения. Если говорить точнее, исходный ключ не всегда легко обнаружить. Для этого может потребоваться небольшой интуитивный щелчок. Однако в целом та же пошаговая схема сохраняется во всех случаях.
А теперь, давайте на примере самого известного математического ребуса - криптарифма рассмотрим цепочку логических рассуждений приводящих к его решению.
Задача 2. SEND+MORE=MONEY
Как решить известный математический ребус - криптарифм SEND+MORE=MONEY
Прежде всего, классифицируем этот ребус как "буквенный математический ребус - криптарифм" в котором использовано 8 различных букв (допустимо не более 10). Для удобства дополним ребус строкой сверху, в которой будем отмечать перенос из младших разрядов ("в уме"). Зелёным цветом будем отмечать значения установленные окончательно. Жёлтым цветом будем отмечать предположения. Красным - ошибки.
Для удобства решения, можно записать в строчку или столбец от 0 до 9 для того, чтобы видеть цифры, которые свободны и вычеркивать те, которые заняты.
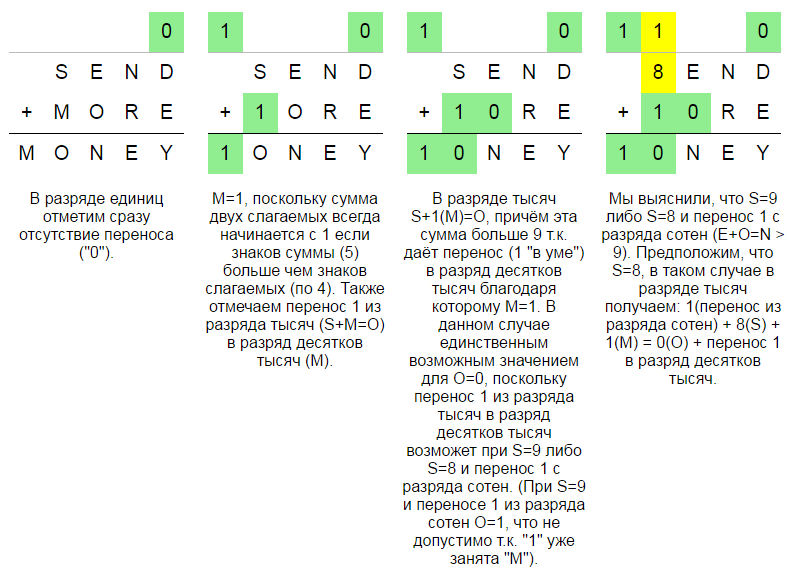
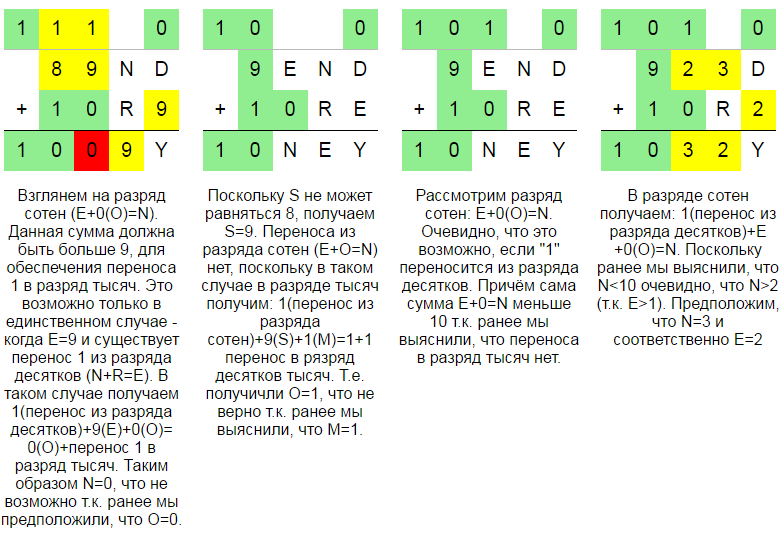
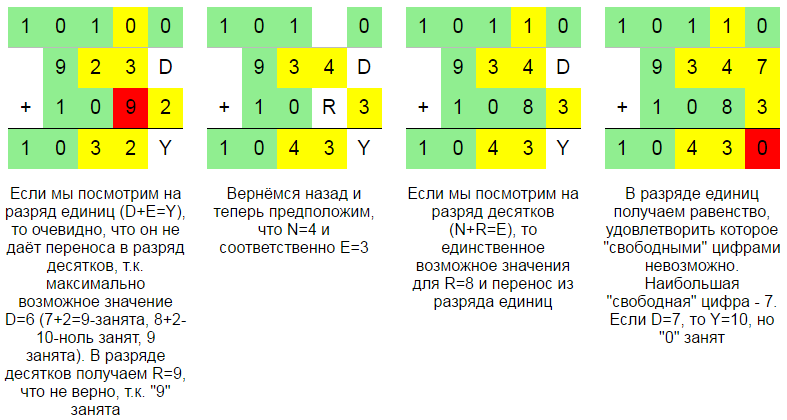
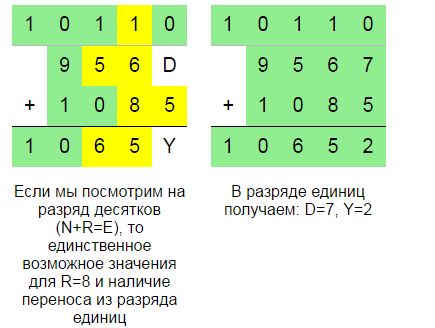
Рассмотрим ещё несколько задач.
Задача 3. Число палиндром
Умножив два числа, получаем число, обратное первому множителю. Что это за числа?
Замечаем, что
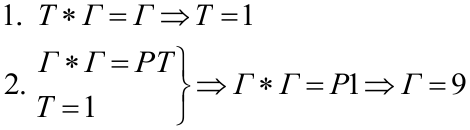
Получили:
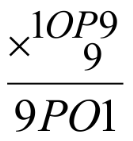
3. Так как при умножении четырехзначного числа (первая цифра, которого равна 1) на 9, получаем четырехзначное число первая цифра, которого равна 9, следовательно, вторая цифра (первого множителя) может быть только 0 или 1 при умножении на 9 (иначе число-результат будет пятизначным числом ). Но 1 мы уже использовали, поэтому буква О – это цифра 0. Т.е. получаем
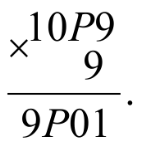
4. Осталось найти букву Р. Начнем умножать столбиком: 9*9=81.1 пишем в разряд единиц, 8 переносим в следующий разряд
т. е. при умножении Р на 9 число единиц равно 2. Следовательно Р=8. Таким образом, получаем:1089*9=9801.
Задача 4. Каникулярная
1. Сумма двух целых положительных однозначных чисел не может превосходить 18, поэтому при поразрядном сложении двух чисел в высший разряд может быть перенесена лишь 1. Отсюда П=1, а Л, Е, Т, О не равны 1.
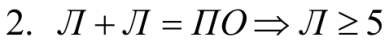
3. 
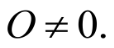Так как если бы О=0, то О+О=О, а у нас О+О=Т.
4. О+О=Т, следовательно Т- четное.
5. Л не равно 5. Так как если бы Л=5, то
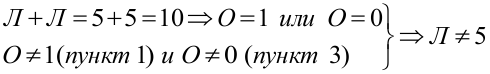
6. Л не равно 6. Так как если бы Л=6, то
7. Л не равно 7. Так как если бы Л=7, то
8. Л=8. Так как
9. Л не равно 9. Так как если бы Л=9, то
Получаем: 8947+8947=17894
Задача 5. Умножение
Первый множитель – число большее 90. Так как, если бы первый множитель был меньше 90, то умножая его на двузначное число ( второй множитель), меньшее 100, получили бы число, меньшее 90*100=9000. Но если первый множитель больше 90, то вторая цифра второго множителя 1 (третья строка двузначное – число), а первая – 9. Если допустить, что она меньше 9, например, 8, то умножая 81 на первый множитель (двузначное число), меньшее 100, получим в произведении число, меньшее 81*100=8100. Получаем, второй множитель равен 91. Пусть первый множитель равен 98, тогда 98*91=8918. Не подходит, так как произведение – 4-значное число, большее 9000.Окончательно получаем 99*91=9009.
infourok.ru
|
|
|
|
|
|
.jpg)
