Арифметика изучает числа, их виды (натуральные, действительные, комплексные, рациональные, целые), арифметические действия, выполняемые над ними (сложение, вычитание, умножение, деление), а так же свойства чисел.
Наука арифметика появилась из-за потребности в счете, и огромный вклад в ее развитие внесли греческие ученые.
Арифметика изучает самые элементарные свойства чисел, то, как эти числа можно записывать, а также действия, которые можно выполнять с этими числами. Существует также учебный предмет с одноименным названием.
Происходит слово quot;арифметикаquot; от греческого слова arithmos, что в переводе означает quot;числоquot;. Соответственно и объект изучения арифметики - это число.
Арифметика - это наука, изучающая действия над числами, изучающая правила обращения с ними. Наука эта обучает решению задач, которые сводятся к вычитанию, сложению, делению и умножению. То есть получается, что арифметика учит азам счета.
Слово Арифметика происходит от греческого слова arithmos число). Это наука о числах и разных операциях над ними. Арифметика изучает натуральные и дробные числа, эта наука является одной из древних отраслей человеческого знания.
Арифметика тесно связана с такими науками как алгебра, геометрия и теория чисел (последнюю еще называют высшей арифметикой).
Изучать арифметику начинают с начальных классов школы, даже с детского сада.
Арифметика ничего не изучает. Арифметика это инструмент для изучения чего либо нового, неизвестного. А в арифметике все известно. Например, что можно изучать в отвертке? Когда-то, на заре становления это была наука. Так же, как например астрология. Раньше это была наука - изучала влияние положения планет на судьбу человека, теперь, когда доказано, что никакого влияния нет - это просто один из видов досуга.
Арифметика в переводе с древнегреческого означает число. Соответственно, арифметика, изучает числа, их свойства и действия с ними - сложение, вычитание, умножение, деление. Можно сказать, что арифметика, это начальный раздел математики.
Арифметика-это раздел математики,изучающий простые виды чисел-целые,натуральные и рациональные,и действия с этими числами-сложение,вычитание,умножение,деление.Является одной из основных математических наук.
Арифметика это часть математики. Арифметика изучает числа. Наука арифметика была известна ещ до нашей эры. И берт свое название с греческого языка. Основные способы работы с числами в арифметике это сложение, умножение, вычитание и деление.
Наиболее правильным определением будет следующее:

На сегодняшний день, насколько мне известно, арифметику переименовали в математику, с 1 по 6 классы. Начиная с 7 и до 11 математику конкретизируют и разделяют на два предмета - алгебру и геометрию.
Арифметика это один из разделов в математике, который изучает числа, их свойства и отношения. Арифметика вводит в понятие о числах (натуральные, целые и т.д.) и их свойствах, рассматривает элементарные операции (сложение, вычитание и т.д.), приемы вычислений и измерения.
info-4all.ru

7 Найдите в учебнике, справочной литературе или Интернете ответы на следующие вопросы:От какого слова происходит слово «арифметика»?
Арифметика – от древнегреческого – число
Что изучает арифметика?
Арифметика — раздел математики, изучающий числа, их отношения и свойства.
В какое время и где жил Диофант – автор наиболее известного в древние времена учебника «Арифметика»?
Диофа́нт Александри́йский— древнегреческий математик, родился предположительно в III веке н. э. Жил в Александрии (Египет)
В каком году вышло первое издание известного в России учебника «Арифметика» Леонтия Филипповича Магницкого?
В 1703 году Магницкий Л. Ф. составил первую в России учебную энциклопедию по математике под заглавием «Арифметика, сиречь наука числительная с разных диалектов на славенский язык переведеная и во едино собрана, и на две книги разделена» тираж 2400 экземпляров.Как учебник эта книга более полувека употреблялась в школах.
В каких странах число нуль считают натуральным числом?
Во французской традиции, восходящей к работам Н. Бурбаки, в отличие от других математических школ натуральными принято считать числа, выражающие количество предметов в группе. Поэтому в этой традиции наименьшим натуральным числом считается ноль («0»), а не единица, и, соответственно, французские математики, в отличие от других, признают ноль натуральным числом.
8 В те далекие времена, когда счет не был хорошо развит, слово «семь» использовалось также в значении «много», что отражено в поговорках и загадках, например: семеро одного не ждут; семь одежек и все без застежек. Приведите как можно больше таких примеров.
Семеро с ложкой, один – с сошкойСемь раз отмерь, один раз отрежь.За семь вёрст киселя хлебать.Семеро одну соломинку подымают.Семь вёрст до небес и все лесом.Потерял пять, а нашёл семьЗа семью печатямиС одной коровы семь шкур не дерут.Седьмая вода на киселе.Семеро по лавкам сидят.Семи пядей во лбу.Семь бед — один ответ.
playroom.ru
Что такое арифметика? Когда человечество начало использовать числа и работать с ними? Куда уходят корни таких обыденных понятий, как числа, дроби, вычитание, сложение и умножение, которые человек сделал неотделимой частью своей жизни и мировоззрения? Древнегреческие умы восхищались такими науками, как математика, арифметика и геометрия, как прекраснейшими симфониями человеческой логики.

Возможно, арифметика не так глубока, как другие науки, но что было бы с ними, забудь человек элементарную таблицу умножения? Привычное нам логическое мышление, использующие цифры, дроби и другие инструменты, нелегко давалось людям и долгое время было недоступно для наших предков. Фактически до развития арифметики ни одна область человеческого знания не была по-настоящему научной.
Арифметика – это наука о числах, с которой любой человек начинает знакомство с увлекательным миром математики. Как говорил М. В. Ломоносов, арифметика – это врата учености, открывающие нам путь к миропознанию. А ведь он прав, разве познание мира можно отделить от знания цифр и букв, математики и речи? Возможно, в былые времена, но не в современном мире, где бурное развитие науки и техники диктует свои законы.
Слово "арифметика" (греч. "арифмос") греческого происхождения, обозначает "число". Она изучает число и все что может быть с ними связано. Это мир чисел: различные действия над числами, числовые правила, решение задач, которые связаны с умножением, вычитанием и т. д.

Общепринято считать, что арифметика является начальной ступенькой математики и твердой основой для более сложных ее разделов, таких, как алгебра, матанализ, высшая математика и т. д.
Основа арифметики – это целое число, свойства и закономерности которого рассматриваются в высшей арифметике или теории чисел. По сути, от того, насколько верный подход взят в рассмотрении такого небольшого блока, как натуральное число, зависит прочность всего здания – математики.

Поэтому на вопрос о том, что такое арифметика, можно ответить просто: это наука о числах. Да, о привычной семерке, девятке и всем этом разнообразном сообществе. И подобно тому, как и хороших, и самых посредственных стихов не напишешь без элементарной азбуки, без арифметики не решить даже элементарной задачи. Вот почему все науки продвинулись только после развития арифметики и математики, будучи до этого всего лишь набором предположений.
Что такое арифметика - натуральная наука или фантом? На самом деле, как рассуждали древнегреческие философы, ни чисел, ни фигур в реальности не существует. Это всего лишь фантом, который создается в человеческом мышлении при рассматривании окружающей среды с ее процессами. В самом деле, что такое число? Нигде вокруг мы не видим ничего подобного, что можно было бы назвать числом, скорее, число - это способ человеческого разума изучать мир. А может быть, это изучение нас самих изнутри? Об этом спорят философы много веков подряд, поэтому дать исчерпывающий ответ мы не беремся. Так или иначе, арифметике удалось настолько прочно занять свои позиции, что в современном мире никто не может считаться социально адаптированным без знания ее основ.
Конечно, основной объект, которым оперирует арифметика, – натуральное число, такое, как 1, 2, 3, 4, …, 152... и т.д. Арифметика натуральных чисел является результатом счета обычных предметов, например, коров на лугу. Все-таки определение "много" или "мало" когда-то перестало устраивать людей, и пришлось изобретать более совершенные техники счета.

Но настоящий прорыв случился, когда человеческая мысль дошла до того, что можно одним и тем же числом «два» обозначить и 2 килограмма, и 2 кирпича, и 2 детали. Дело в том, что нужно абстрагироваться от форм, свойств и смысла предметов, тогда можно производить некоторые действия с этими предметами в виде натуральных чисел. Так родилась арифметика чисел, которая дальше развивалась и ширилась, занимая все большие позиции в жизни общества.
Такие углубленные понятия числа, как ноль и отрицательное число, дроби, обозначения чисел цифрами и другими способами, имеют богатейшую и интереснейшую историю развития.
Два древнейших спутника человека в исследовании окружающего мира и решении бытовых задач – это арифметика и геометрия.

Считается, что история арифметики берет свое начало на Древнем Востоке: в Индии, Египте, Вавилоне и Китае. Так, папирус Ринда египетского происхождения (назван так, поскольку принадлежал одноименному владельцу), датируемый XX в. до н.э, кроме других ценных данных содержит разложение одной дроби на сумму дробей с разными знаменателями и числителем, равным единице.
Например: 2/73=1/60+1/219+1/292+1/365.
Но в чем смысл такого сложного разложения? Дело в том, что египетский подход не терпел абстрагированных размышлений о числах, наоборот, вычисления производились только с практической целью. То есть египтянин станет заниматься таким делом, как расчеты, исключительно для того, чтобы построить гробницу, например. Нужно было высчитать длину ребра сооружения, и это заставляло садиться человека за папирус. Как видно, египетский прогресс в расчетах был вызван, скорее массовым, строительством, нежели любовью к науке.
По этой причине расчеты, найденные на папирусах, нельзя назвать размышлениями на тему дробей. Скорее всего, это практическая заготовка, которая помогала в дальнейшем решать задачи с дробями. Древние египтяне, не знавшие таблицы умножения, производили довольно длинные вычисления, разложенные на множество подзадач. Возможно, это одна из таковых подзадач. Нетрудно заметить, что расчеты с такими заготовками весьма трудоемки и малоперспективны. Может быть, по этой причине мы не видим большого вклада Древнего Египта в развитие математики.
Многие знания Древнего Востока были успешно освоены древними греками, известными любителями отвлеченных, абстрактных и философских размышлений. Практика их интересовала не меньше, но лучших теоретиков и мыслителей найти сложно. Это пошло на пользу науке, поскольку в арифметику невозможно углубиться, не разорвав ее с реальностью. Конечно, можно умножать 10 коров и 100 литров молока, но далеко продвинуться не удастся.

Мыслящие глубоко греки оставили значительный след в истории, и их труды дошли до нас:
И, конечно, превращающие все в философию греки, а особенно продолжатели дела Пифагора, настолько были увлечены числами, что считали их таинством гармонии мира. Числа настолько были изучены и исследованы, что некоторым из них и их парам приписывали особые свойства. Например:

Греки, считавшие, что науку нужно любить, а не быть с ней ради выгоды, достигли больших успехов, исследуя, играя и складывая числа. Нужно отметить, что не все их изыскания нашли широкое применение, некоторые из них остались лишь "для красоты".
Точно так же и в Средние века арифметика своим развитием обязана восточным современникам. Индийцы передали нам цифры, которые мы активно используем, такое понятие как "нуль", и позиционный вариант системы исчисления, привычный современному восприятию. От Аль-каши, который в 15 веке работал в Самарканде, мы унаследовали десятичные дроби, без которых трудно представить современную арифметику.
Во многом знакомство Европы с достижениями Востока стало возможно благодаря труду итальянского ученого Леонардо Фибоначчи, который написал произведение "Книга абака", знакомящее с восточными новшествами. Оно стало краеугольным камнем развития алгебры и арифметики, исследовательской и научной деятельности в Европе.
И, наконец, арифметика, нашедшая свое место и укоренившаяся в Европе, стала распространяться и на русские земли. Первая русская арифметика вышла в 1703 году – это была книга об арифметике Леонтия Магницкого. Долгое время она оставалась единственным учебным руководством по математике. Она содержит начальные моменты алгебры и геометрии. Цифры, которые использовал в примерах первый в России учебник арифметики, арабские. Хотя арабские цифры встречались и ранее, на гравюрах, датирующихся 17 веком.
Сама книга украшена изображениями Архимеда и Пифагора, а на первом листе - образ арифметики в виде женщины. Она сидит на престоле, под ней написано на иврите слово, обозначающее имя Бога, а на ступенях, которые ведут к престолу, начертаны слова «деление», «умножение», «сложение» и т. д. Можно только представить, какое значение предавали таким истинам, которые сейчас считаются обыденным явлением.
Учебник из 600 страниц описывает как основы вроде таблицы сложения и умножения, так и приложения к навигационным наукам.
Не удивительно, что автор выбрал изображения греческих мыслителей для своей книги, ведь он и сам был пленен красотой арифметики, говоря: «Арифметика есть числительница, есть художество честное, независтное… ». Такой подход к арифметике вполне обоснован, ведь именно ее повсеместное внедрение можно считать началом бурного развития научной мысли в России и общего образования.
Простое число – это такое натуральное число, которое имеет только 2 положительных делителя: 1 и само себя. Все остальные числа, не считая 1, называют составными. Примеры простых чисел: 2, 3, 5, 7, 11, и все другие, которые не имеют прочих делителей, кроме числа 1 и себя самого.
Что же касается числа 1, то оно на особом счету – существует уговор, что его нужно считать ни простым, ни составным. Простое на первый взгляд простое число таит множество неразгаданных тайн внутри себя.
Теорема Евклида говорит, что простых чисел бесконечное множество, а Эратосфен придумал специальное арифметическое «решето», которое отсеивает непростые числа, оставляя только простые.
Ее суть в том чтобы подчеркивать первое невычеркнутое число, а в последующем вычеркивать те, которые ему кратны. Многократно повторяем эту процедуру - и получаем таблицу простых чисел.
Среди наблюдений о простых числах нужно особым образом упомянуть основную теорему арифметики.
Основная теорема арифметики гласит, что любое целое число, большее 1, либо является простым, либо его можно разложить на произведение простых чисел с точностью до порядка следования сомножителей, причем единственным образом.
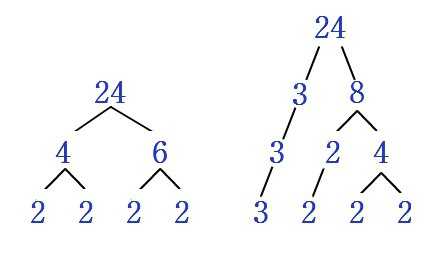
Основная теорема арифметики доказывается достаточно громоздко, да и понимание ее уже не похоже на простейшие основы.
На первый взгляд простые числа - элементарное понятие, однако это не так. Физика также некогда считала атом элементарным, пока не нашла внутри него целую вселенную. Простым числам посвящен прекрасный рассказ математика Дона Цагира «Первые пятьдесят миллионов простых чисел».
Что поистине можно назвать армированным фундаментом всей науки – это законы арифметики. Еще в детстве все сталкиваются с арифметикой, изучая количество ножек и ручек у кукол, количество кубиков, яблочек и т. д. Так мы изучаем арифметику, которая дальше переходит в более сложные правила.

Вся наша жизнь знакомит нас с правилами арифметики, которые стали для простого человека наиболее полезными из всего, что дает наука. Изучение чисел - это "арифметика-малышка", которая знакомит человека с миром чисел в виде цифр еще в раннем детстве.
Высшая арифметика - дедуктивная наука, которая изучает законы арифметики. Большинство из них нам известно, хотя, возможно, мы и не знаем их точных формулировок.
Два любых натуральных числа a и b могут быть выражены в виде суммы a+b, которая также будет числом натуральным. Касательно сложения действуют следующие законы:
Правила арифметики, такие, как сложение, - одни из элементарных, но их используют все науки, не говоря уже о повседневной жизни.
Два любых натуральных числа a и b могут быть выражены в произведении a*b или a*b, которое также является числом натуральным. К произведению применимы те же коммутативные и ассоциативные законы, что и к сложению:
Интересно, что существует закон, который объединяет сложение и умножение, называемый также распределительным, или дистрибутивным законом:
a(b+c)= ab+ac
Этот закон фактически учит нас работать со скобками, раскрывая их, тем самым мы можем работать уже с более сложными формулами. Это именно те законы, которые будут вести нас по причудливому и непростому миру алгебры.
Закон порядка человеческая логика использует каждый день, сверяя часы и считая купюры. И, тем не менее, и его нужно оформить в виде конкретных формулировок.
Если мы имеем два натуральных числа a и b, то возможны следующие варианты:
Из трех вариантов справедливым может быть только один. Основной закон, который управляет порядком, говорит: если a < b и b < c, то a< c.
Существуют также и законы, связывающие порядок с действиями умножения и сложения: если a< b, то a + c < b+c и ac< bc.
Законы арифметики учат нас работать с числами, знаками и скобками, превращая все в стройную симфонию чисел.
Можно сказать, что числа – это математический язык, от удобства которого зависит многое. Существует множество систем исчисления, которые, как и алфавиты разных языков, отличаются между собой.
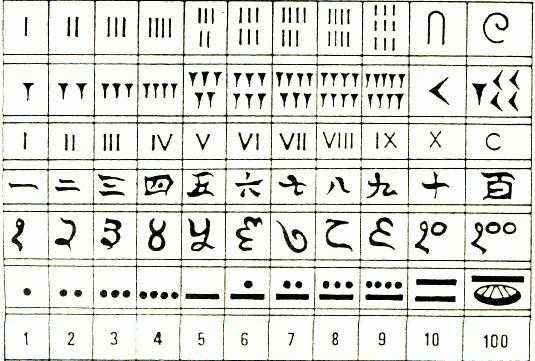
Рассмотрим системы счисления с точки зрения влияния позиции на количественное значение цифры на этой позиции. Так, например, римская система является непозиционной, где каждое число кодируется определенным набором специальных символов: I/ V/ X/L/ C/ D/ M. Они равны, соответственно, числам 1/ 5/10/50/100/500/1000. В такой системе цифра не изменяет своего количественного определения в зависимости от того, на какой она стоит позиции: первой, второй и т. д. Чтобы получить другие числа, нужно сложить базовые. Например:
Более привычная для нас система счисления с использованием арабских цифр является позиционной. В такой системе разряд числа определяет количество цифр, например, трехразрядные числа: 333, 567 и т.д. Вес любого разряда зависит от позиции, на которой находится та или иная цифра, например цифра 8 на второй позиции имеет значение 80. Это характерно для десятичной системы, существуют и другие позиционные системы, например двоичная.
Нам знакома десятичная система исчисления, состоящая из одноразрядных чисел и многоразрядных. Цифра слева у многоразрядного числа в десять раз больше по значимости той, которая справа. Так, мы привыкли читать 2, 17, 467 и т. д. Совершенно другая логика и подход у раздела, который носит название "двоичная арифметика". Это и неудивительно, ведь двоичная арифметика создана не для человеческой логики, а для компьютерной. Если арифметика чисел произошла от счета предметов, что в дальнейшем абстрагировалось от свойств предмета к "голой" арифметике, то с компьютером такое не пройдет. Чтобы можно было поделиться своими знаниями с ЭВМ, человеку пришлось изобрести такую модель исчисления.

Двоичная арифметика работает с двоичным алфавитом, который состоит всего из 0 и 1. А использование этого алфавита называется двоичной системой исчисления.
Отличие двоичной арифметики от десятичной в том, что значимость позиции слева больше не в 10, а в 2 раза. Двоичные числа имеют вид 111, 1001 и т. д. Как понимать такие числа? Итак, рассмотрим число 1100:
То есть при переходе на новый разряд слева его значимость в двоичной системе умножается на 2, а в десятичной - на 10. Такая система имеет один минус: это слишком большой рост разрядов, которые необходимы для записи чисел. Примеры представления десятичных чисел в виде двочиных можно посмотреть в следующей таблице.
Десятичные числа в двоичном виде изображены ниже.

Используются также и восьмеричная, и шестнадцатеричная системы исчисления.
Что такое арифметика, «дважды два» или неизведанные тайны чисел? Как видим, арифметика, может, и кажется на первый взгляд простой, но ее неочевидная легкость обманчива. Ее можно изучать и детям вместе с тетушкой Совой из мультика «Арифметика-малышка», а можно погрузиться в глубоко научные изыскания чуть ли не философского порядка. В истории она прошла путь от счета предметов до поклонения красоте чисел. Одно только точно известно: с установлением основных постулатов арифметики вся наука может опираться на ее крепкое плечо.
fb.ru
Слово «арифметика» происходит от греческого arithmos, что значит «число» . Эта наука изучает действия над числами, различные правила обращения с ними, учит решать задачи, сводящиеся к сложению, вычитанию, умножению и делению чисел. Часто представляют себе арифметику как некоторую первую ступень математики, основываясь на которой можно изучать более сложные ее разделы - алгебру, анализ математический и т. д. Даже целые числа - основной объект арифметики - относят, когда рассматривают их общие свойства и закономерности, к высшей арифметике, или теории чисел. Такой взгляд на арифметику, конечно, имеет основания - она действительно остается «азбукой счета» , но азбукой «многополезнейшей» и «удобнопонятной» . (в переводе с латыни: "сосновая шишка" - "конус", "валик" - "цилиндр", "столик" - "трапеция", "бубен" - "ромб"
Арифме́тика (др. -греч. ἀριθμητική от ἀριθμός — число) — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа в развитии представлений о нём (натуральные, целые и рациональные, действительные, комплексные числа) и его свойствах. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук, она тесно связана с алгеброй, геометрией и теорией чисел
Арифметика - от греч. арифмос - число.
с греческого число
с греческого языка Арифметика - число
Слово «арифметика» происходит от греческого arithmos, что значит «число». Эта наука изучает действия над числами, различные правила обращения с ними, учит решать задачи, сводящиеся к сложению, вычитанию, умножению и делению чисел.
спасибо большое что сказали не правильно
дебилы вы все лохи пидары гандоны пиздаболы
карл +++ Пиздаболы ебанные
Арифме́тика (др. -греч. ἀριθμητική; от ἀριθμός – число) — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа в развитии представлений о нём (натуральные, целые и рациональные, действительные, комплексные числа) и его свойствах. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел
Слово «арифметика» происходит от греческого arithmos, что значит «число» . Эта наука изучает действия над числами, различные правила обращения с ними, учит решать задачи, сводящиеся к сложению, вычитанию, умножению и делению чисел. Часто представляют себе арифметику как некоторую первую ступень математики, основываясь на которой можно изучать более сложные ее разделы - алгебру, анализ математический и т. д. Даже целые числа - основной объект арифметики - относят, когда рассматривают их общие свойства и закономерности, к высшей арифметике, или теории чисел. Такой взгляд на арифметику, конечно, имеет основания - она действительно остается «азбукой счета» , но азбукой «многополезнейшей» и «удобнопонятной» . (в переводе с латыни: "сосновая шишка" - "конус", "валик" - "цилиндр", "столик" - "трапеция", "бубен" - "ромб"
где жил диофант и в какое время
<img src="//otvet.imgsmail.ru/download/176914974_fc6ff21c5b87d4e14643db9d3cbd2542_800.jpg" alt="" data-lsrc="//otvet.imgsmail.ru/download/176914974_fc6ff21c5b87d4e14643db9d3cbd2542_120x120.jpg" data-big="1">
арифметика это арифметика
Слово «арифметика» происходит от греческого arithmos, что значит «число» . Эта наука изучает действия над числами, различные правила обращения с ними, учит решать задачи, сводящиеся к сложению, вычитанию, умножению и делению чисел. Часто представляют себе арифметику как некоторую первую ступень математики, основываясь на которой можно изучать более сложные ее разделы - алгебру, анализ математический и т. д. Даже целые числа - основной объект арифметики - относят, когда рассматривают их общие свойства и закономерности, к высшей арифметике, или теории чисел. Такой взгляд на арифметику, конечно, имеет основания - она действительно остается «азбукой счета» , но азбукой «многополезнейшей» и «удобнопонятной» . (в переводе с латыни: "сосновая шишка" - "конус", "валик" - "цилиндр", "столик" - "трапеция", "бубен" - "ромб"
touch.otvet.mail.ru