 Продолжаю публиковать числовые ребусы. Сегодня, уважаемые читатели сайта ВСЕ РАЗГАДАЕМ, предлагаю вашему вниманию 10 ребусов с числом 100. Предложенные ребусы будут разной степени сложности, требующие разного подхода к разгадыванию. Но объединит все эти ребусы, конечно же, прекрасное число – 100 🙂 .
Продолжаю публиковать числовые ребусы. Сегодня, уважаемые читатели сайта ВСЕ РАЗГАДАЕМ, предлагаю вашему вниманию 10 ребусов с числом 100. Предложенные ребусы будут разной степени сложности, требующие разного подхода к разгадыванию. Но объединит все эти ребусы, конечно же, прекрасное число – 100 🙂 .
Начинаю с самых простых ребусов:
Ребус с числом 100 № 1
Ребус с числом 100 № 2
Переходим к более сложным числовым ребусам. Как вы заметили, в данных ребусах используются еще и картинки:
Числовой ребус № 3

Числовой ребус, ребус с числом 100 № 4
Если вы обратите внимание, то увидите, что у следующих двух ребусов с числительными есть одно сходство (общее число 100 и цвет фона – не считается).
Числовой ребус № 5
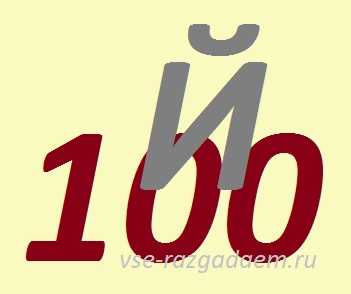
Числовой ребус № 6

Ну и «на закуску» - самые интересные ребусы с числом 100:
Ребус с числом 100 № 7

Числовой ребус № 8
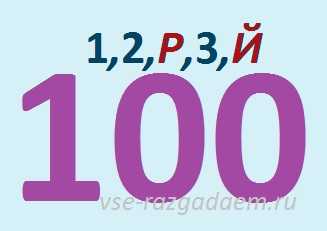
Числовой ребус № 9

Десятый ребус с числом 100 расположен в самом начале этой статьи. Приятного вам разгадывания!
Примечание: ответы к числовым ребусам этой статьи опубликую в конце следующей статьи с числовыми ребусами.
Предлагаю также ребусы с цифрами от 1 до 10.
Ну а теперь, в конце статьи, как обещала, рассказ с подсказками-ответами к ребусам о весне.
Пришла весна. Стало ярче светить … (ребус № 1). Все: и растения, и животные, и люди испытали большую … (ребус № 2) от того, что стало … (ребус № 3). Повсюду побежали … (ребус № 4). Набухли … (ребус № 5). Стали возвращаться … (ребус № 6). А женщины с удовольствием принимали в подарок прекрасные веточки … (ребус № 7), похожие на весеннее яркое солнышко.
vse-razgadaem.ru
К ребусам такие головоломки не имеют никакого отношения, но исторически сложилось, что подобные задачки называют именно так.
Это примеры обычных арифметических действий (на сложение, вычитание, умножение, деление, иногда возведение в степень и извлечение корня), в которых все или большая часть цифр заменена какими-либо символами или буквами. В буквенном арифметическом ребусе каждая буква означает одну определённую цифру. В символьных ребусах со звёздочками, кружочками и точками каждый значок может обозначать любую цифру от 0 до 9. Причём цифры могут повторяться, какие-то могут вообще не использоваться. Единственное исключение - числа не начинаются на 0. Иногда вместо всего числа ставят знак «?», то есть даже сколько цифр в числе не известно. Решить такой ребус - это значит восстановить первоначальную запись примера.
При решении задач такого типа требуется внимательность к очевидным арифметическим действиям, хорошее знание арифметики и умение логически рассуждать. Арифметика - это не только 2+2=4. Это также глубокое понимание принципов порядкового исчисления, знание правил раскрытия скобок, признаков делимости, разложения на множители, правил действия с дробями и степенями, пропорциями, что такое натуральные, простые и составные числа, как найти НОК и НОД, как посчитать сумму последовательности и многое другое.
Некоторые математические задачи могут оказаться слишком сложными для использования в обычных (не математических) квестах, поэтому выбирать их следует внимательно.
Арифметических ребусов, как и обычных ребусов, - бесконечное множество. Но все их можно поделить на несколько видов.
В таких арифметических ребусах все цифры заменены на точки, звёздочки, кружочки, в общем, на одинаковые символы.
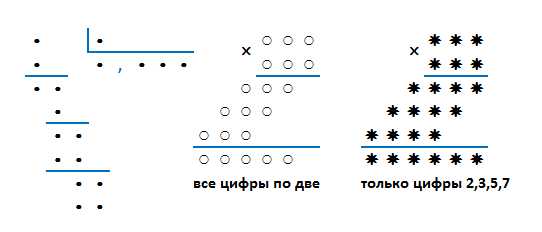
В обычных «пустышках» часто для подсказки открывают некоторые цифры, либо какую-то из цифр (какую точно, не известно) помечают специальным знаком. Получаются «пустышки с подсказками».
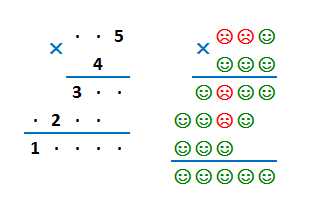
Чётные цифры (0,2,4,6,8) помечены буквой Ч, а нечётные (1,3,5,7,9) - буквой Н.
Это классика математических ребусов, в них цифры заменены буквами. Чаще всего авторы подобных задач стараются так подобрать буквы, чтобы в отдельных местах читались слова. Остальные же места, где слова не получаются, остаются, как в пустышках. Иногда в некоторых местах также оставляют подсказки.
У нас есть 10 цифр, а в русском языке довольно много слов, состоящих из 10-ти разных неповторяющихся букв. Их можно использовать как ключевые слова в головоломках, которые некоторые называют «ребусы с ключевыми словами», а я называю «Рамки».
Каждая такая задачка состоит из 6-ти уравнений, связанных между собой знаками « + », « – », « x », « : », « = ». Цифры зашифрованы буквами, разным цифрам соответствуют разные буквы. Обычно используется 10 букв для 10-ти цифр, но можно составить пример и из меньшего количества цифр, тогда и букв будет меньше.
Это настоящая математическая задача, причём довольно сложная, поэтому подойдёт не для каждого квеста.
Решается задача так.
Рассмотрим первый столбец ПЗ+УУ=ИГЕ. Сумма двух двузначных чисел не может быть больше 99+99=198, значит, И=1.
В равенстве ПЕП-ЗТ=ИНЗ (третий столбец) видно, что к трёхзначному числу, начинающемуся на 1, прибавили двузначное число. П - не 1, так как 1 уже занято буквой И. Выходит, П=2.
В третьей строке ИГЕ+НО=ИНЗ при сложении Г десятков с Н десятками снова получается Н десятков. Это может быть только если Г=0 или Г=9. Но если бы Г было равно 9, то был бы перенос единицы в разряд сотен, а у нас было И и осталось И. Значит, Г=0.
Итак, Г=0, И=1, П=2. А поэтому в равенстве ПЗ+УУ=ИГЕ У может быть или 7, или 8, ведь нам надо к двум с чем-то десяткам прибавить двузначное число, и чтобы получилось больше сотни. Пусть, У=8. Тогда из УУ+У=ЗТ следует, что Т=6 и З=9. Но тогда в разности ПЕП-ЗТ=ИНЗ получаем П=5. Но ведь П=2! Значит, У≠8. Следовательно, У=7. Тогда из УУ+У=ЗТ получаем Т=4, З=9. Равенство ПЗ+УУ=ИГЕ при З=8 и У=7 даёт нам ещё одну букву: Е=5.
В сумме ИГЕ+НО=ИНЗ Е=5, З=8, а значит, О=3. В третьем столбце нам уже стали известны все буквы, кроме Н. Поэтому, значение её легко находится: Н=6. И, наконец, из равенства АxУ=НО получаем А=9.
В результате имеем: 0123456789=ГИПОТЕНУЗА. Слово разгадано, его можно как-то использовать дальше в виде ключевого слова или подсказки для решения следующих квестовых задач.
Ниже приведены примеры «математических ребусов».
Ответы: 1-гипотенуза, 2-справочник, 3-демократия, 4-крестовина, 5-струбцина, 6-хлопчатник, 7-деформация, 8-заповедник, 9-лесотундра, 10-метилоранж, 11-проявитель, 12-экспертиза, 13-вольфрамит, 14-пятидневка, 15-республика, 16-дегустация, 17-дешифровка, 18-подсвечник, 19-глубиномер, 20-трудолюбие, 21-фильмотека, 22-погремушка, 23-ускоритель, 24-демография, 25-центрифуга, 26-манускрипт, 27-эскадрилья, 28-меблировка, 29-этнография, 30-умывальник, 31-Лев Яшин, 32-сподумен.
Внешний вид задачек такого рода напоминает столбики, сложенные из кирпичей, поэтому назову их «кирпичики».
Правила такие:
каждый квадратик - это одна цифра;
ни одно число не начинается на 0;
сумма чисел каждого вертикального ряда равна результату соответствующей горизонтальной строки;
действия производятся последовательно слева направо, то есть правила приоритета не работают.
Решим для примера вот такие «кирпичики»:
Для начала, используя правило [3], зеркально относительно диагонали отразим и дополним результаты столбцов и строк. Шестёрка из результата второго столбца скопируется во вторую строку, а тройка из результата первой строки скопируется в первый столбец.
Посмотрим на вторую строку. Первые два числа однозначные, значит их сумма не больше 18, а значит отнять можно только 16, иначе у нас получится отрицательное число. Значит, третье число во второй строке 16. Допустим, сумма двух первых чисел 17. Тогда 17-16=1. Один умножить на однозначное число и получается двузначное - так не бывает. Значит, сумма двух первых чисел строки не 17, а 18. Значит, это обе девятки, 9+9-16=2. А на какое однозначное число надо умножить двойку, чтобы получилось двузначное с шестёркой на конце? На 8! Итого, получили целиком вторую строку: 9+9-16×8=16. Не забываем, что порядок действий - слева направо, то есть как будто запись вот такая: [(9+9)-16]×8=16.
Теперь смотрим на второй столбец. 16-2-9=5. То есть третье и четвёртое числа во втором столбце дают в сумме 5. Теперь посмотрим на третью строку. Результат сложения двузначного числа, оканчивающегося семёркой и второго числа должен делиться на 5, а значит должен заканчиваться на 5 или 0. А значит, третье число во втором столбце должно быть или 3 или 8. Но оно ведь должно быть меньше пяти! Значит, это тройка. А тогда четвёртое число во втором столбце - это двойка.
Результат первой строки - это 30 или 35, так как в конце стоит умножение на 5. Значит, сумма первого столбца тоже 30 или 35.
В первом столбце третье число - это 17, или 27, или 37, или т.д. Допустим, 27. Тогда 27+9=36, а это уже больше, чем весь возможный результат столбца - 35. Значит, у нас не 27, а 17. Итого, получилась третья строка: 17+3:5×8=32.
Итак, результат первой строки 30 или 35. Пусть 35. Тогда сумма первых двух чисел равна 7, а третье число - единица. Значит, третий столбец начинается с единицы. Получается, что четвёртое число в третьем столбце должно равняться 32-1-16-5=10. Но оно однозначное! Мы допустили, что результат первой строки 35 и пришли к противоречию. Значит, не 35, а 30.
А раз 30, думаем над первой строкой. Третье число, как мы уже установили, не единица. Значит, двойка. Любого другого будет уже много. Получаем первую строку: 1+2x2x5=30. Ну и тут уже легко получается четвёртая строка: 3+2×9-12=33. И вот он результат:
Как вы заметили, самое нижнее правое число (сумма последней строки, она же сумма последнего столбца) получилось в самом конце решения головоломки. Его невозможно получить в результате промежуточных вычислений, а значит, что такие типы задач можно применять, если в квесте нужно загадать какое-то трёхзначное число. Например, шифр от сейфа. Хотя не, 1000 комбинаций и перебрать можно. Допустим, надо ввести код для отключения бомбы и ошибаться нельзя. Вот тогда три цифры - самый раз .
Ниже набор из 24 готовых «кирпичиков» с ответами:
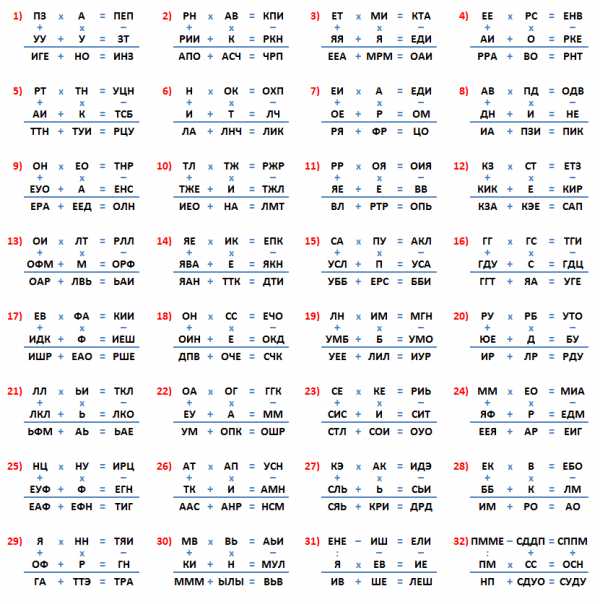
Этот тип задач похож на зашифрованные определённым кодом «кирпичики». Выглядит код так, как будто цифры прикрыли квадратиками, но выступающие части цифр остались видны. Символы, которыми зашифрованы цифры, похожи на амбарные замки, поэтому их так и называют, «замочки» (иногда их называют «коврики», потому что в целом задачка похожа на квадратный вышитый половичок).
Если бы у каждой цифры был свой значок, то это был бы полноценный шифр замены, но здесь один символ соответствует разным цифрам. И понять, какая цифра где скрылась, помогут знания математики. Знаки показывают действия, которые производятся с числами по горизонтали и по вертикали. Последовательность действий такая же, как и в «кирпичиках» - слева-направо и сверху-вниз без учёта приоритета. И решаются «замочки», соответственно, так же, как и «кирпичики». А применять их в квестах можно, например, для открывания «цифровых замочков» на закрытых дверях. Отгадывающим надо будет либо решить такой ребус и узнать правильные 4 цифры, либо перебрать 10000 возможных вариантов комбинаций из 4 цифр.
Разберём пример:
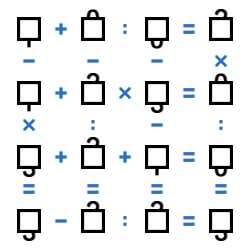
Во второй строке сумма первых двух цифр заведомо больше двух. Третья цифра - это 3, 5 или 9. Результат - однозначное число, значит третья цифра строки 3, а тогда в результате может быть только 9. И значит, первые две цифры - 1 и 2. Получили вторую строку: (1+2)x3=9.
Теперь посмотрим на первый столбец. Первая цифра не равна второй, иначе в результате получился бы ноль. Возможны варианты: 4-1 и 7-1, и оба они больше 2, а третья цифра - 3,5 или 9. Значит, первая цифра - 4, третья - 3, а в результате 9. Получаем (4-1)x3=9.
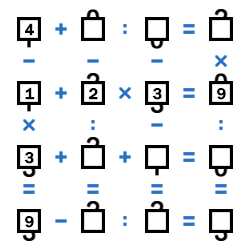
В третьей строке третья цифра не может быть равна 7, иначе в результате получилось бы двузначное число. Не может она быть и 4, так как при второй цифре 2 или 3 в результате было бы 9 или 10, а это не подходит. Значит, третья цифра третьей строки - это 1. Тогда вторая цифра - это 2, а результат - 6, т.е. 3+2+1=6.
Третий столбец отличается от третьей строки только взаимным расположением цифр, поэтому для третьего столбца получаем 6-3-1=2.
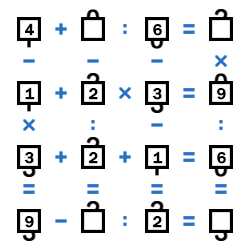
Смотрим на первую строку. В результате 2 или 3, а значит делится на 6 число 12 или 18. 18-4=14 не подходит, значит вторая цифра первой строки - это 8. Получаем первую строку (4+8):6=2.
Осталось посчитать результаты второго и четвёртого столбцов - 3 и 3. Всё, задача решена.
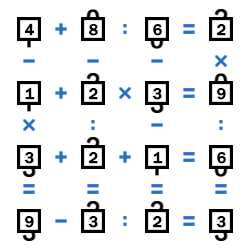
Ниже приведены примеры «замочков» и результаты их решения.
Чтобы не сильно мучиться в отрисовке этих картинок, пришлось немного покодить на яваскрипте (посмотрите исходный код страницы): http://nozdr.ru/coll/carpets.html.
games/quest/math/arith.txt · Последние изменения: 2017/11/25 19:05 — NoZDR
nozdr.ru
Решение числовых ребусовЧисловые ребусы – это примеры, в которых все или некоторые цифры заменены звёздочками или буквами. При этом одинаковые буквы заменяют одинаковые цифры, разные буквы - разные цифры.1.Пусть дан числовой ребус:Решение:Число 8126 является решением ребуса, так как при замене буквы У на цифру 8, буквы Д на 1, буквы А на 2, буквы Р на 6 получается верный пример на сложение.2. Проверьте, является ли число 5621 решением числового ребуса: ^ УДАР + УДАР = ДРАКА.3.Решите числовой ребус: Разберем решение первого ребуса.Сумма И+С (в разряде десятков) оканчивается на С, но ИО (см. разряд единиц). Значит, И = 9 и 1 десяток в разряде единиц запомнили (решение ниже). Теперь легко найти К в разряде сотен: К = 4. Для С остается одна возможность: С = 5.
4.Реши ребус: Решение:В ребусе буква Г обозначает цифру 1, так как при сложении двух пятизначных чисел получается шестизначное число. При этом, чтобы произошел переход через десяток в разряде десятков тысяч, буква К должна обозначать цифру 8 или 9 ( меньше 8 буква К обозначать не может, так как буква Г обозначает цифру 1). Буква К заменяется на цифру 8, если при
сложении чисел произойдёт переход через десяток в разряде тысяч. Независимо от того будет ли буква К заменена на цифру 8 или 9, буква О должна обозначать цифру 0(нуль). Теперь можно выстроить последовательность замены букв цифрами: Г=1; О=0; Р=5; У=4; К=9; А=8; С=3; Д=7.Ответ: 94539+10539=105078
5.Задания для самостоятельной работы.а)б)в)г) Б + БЕЕЕ = МУУУ д) найти значение дроби:Ответы на задания для самостоятельной работы: 6. а) 35977 б) 6823 в) 28375
35977 + 6823 + 28375
71954 13646 28375
85125г) 1+1999 = 2000 Так как при сложении данных чисел цифра Е в разряде десятков поменялась на цифру У , то суммой однозначных чисел Б и Е является двузначное число, начинающееся с единицы. Так как, помимо увеличения на единицу цифры в разряде десятков, так же изменилась и цифра в разряде сотен, то Е=9 и Б=1. Тогда У=0.
д) 0. Поскольку в этом ребусе 10 различных букв, то встречаются все цифры, включая нуль. На нуль делить нельзя, поэтому множитель 0 – в числителе.
infourok.ru
Числовые ребусы
Миллионы людей во всех частях света любят разгадывать ребусы. И это не удивительно. “Гимнастика ума” полезна в любом возрасте. Ведь ребусы тренируют память, обостряют сообразительность, вырабатывают настойчивость, способность логически мыслить, анализировать и сопоставлять.
Вся наша жизнь – беспрерывная цепь игровых ситуаций. Они бывают, значительны, а бывают, пустячны, но и те, и другие требуют от нас принятия решений. Еще в Древней Элладе без игр не мыслилось гармоническое развитие личности. И игры древних не были только спортивными. Наши предки знали шахматы и шашки, не чужды им были ребусы и загадки. Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они и создавали их. С древних времен известны головоломки Пифагора и Архимеда, русского флотоводца С.О. Макарова и американца С. Лойда.
Существует такая разновидность ребусов, которые называются числовыми. Они представляют из себя выражения, требующие арифметического решения, составленные в виде математических равенств, где числа заменяются другими знаками – буквами, фигурками геометрии, звездочками и т.д.
Под числовыми ребусами подразумевают те задачки, в которых необходимо использовать логические рассуждения. Именно они являются способом решения и расшифровывания каждого символа, который ведет к восстановлению числовой записи.
Числовым ребусам уже почти тысяча лет. Впервые они появились в Китае, затем в Индии. В европейских странах числовые ребусы поначалу называли крипт-арифметические задачи. Их появление в Европе впервые было отмечено только в двадцатом веке, несмотря на то, что развитие математики началось много столетий назад.
При составлении ребусов числового типа пользуются следующими правилами. Все использующиеся цифры заменяют буквами. При наличии в задаче одинаковых цифр, соответственно, используется такое же количество букв. Промежуточные стадии математических операций обозначаются звездочками. Различают на основе этих правил несколько типов ребусов. Первый – это ребусы, в которых заменены на цифры все имеющиеся буквы. При этом зашифровывается какое-либо выражение, которое обозначает житейские ситуации в оригинальном изложении.
ТРИ БУЛОК
+ ДВА + БЫЛО
ПЯТЬ МНОГО
СНЕГ МОРЕ ЛЕТО
+ СНЕГ + МОРЕ + ЛЕТО
ВЬЮГА ОКЕАН ТЕПЛО
В записи могут присутствовать не только цифры, но и звездочки, - это второй тип ребусов. Третий тип – это ребусы, в которых практически все символы заменены звездочками.
Числовые ребусы являются очень сложными, порой попадаются такие, которые требуют поэтапного длительного решения. Числовые ребусы являются увлекательными математическими задачами, которые сильно развивают логику и сообразительность.
Числовые ребусы могут быть составлены из нескольких рядов символов, а между ними ставится определенное количество математических знаков, которые являются указателями для того, какие действия необходимо произвести по вертикали, а какие по горизонтали.
1) ТА+ ИТ = ЛЕТ 2) КРА + ОЛИ = ИАЯ
X - + X : -
ЕС х СН = ЛЛАС Л х АР= КЯИ
ЛЕАА + ЕЦ = ЛЕЕЦ ОИИ + АЛ = РКА
Числовые ребусы являются очень популярными не только в школах на обычных уроках, но и на математических олимпиадах. решить числовые ребусы можно с помощью компьютерных программ, однако ни с чем несравнимое удовольствие может получить человек, который самостоятельно ломает голову над разгадкой и в конце концов ее находит.
Задачи, представленные в занимательной форме, очень интересны. Их хочется решать, они увлекают своей необычностью, неочевидностью ответа. Появляется желание совершить пусть даже нелёгкий путь поиска решения. Занимательность и строгость вполне совместимы. Каждое самостоятельно решенное задание – это возможно, небольшая, но всё же победа.
В буквенных ребусах каждой буквой зашифрована одна определенная цифра: одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы.
В ребусах зашифрованных, например, звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе.
Перед началом решения математического буквенного ребуса (например, криптарифма), убедитесь, что в нём использовано не более 10 различных букв. В противном случае, такой ребус не будет иметь решений.
Начните решение ребуса с правила, согласно которому ноль не может быть крайней левой цифрой в числе. Таким образом, все буквы и знаки, с которых начинается число в ребусе, уже не могут обозначать ноль. Круг поиска нужных цифр сузится.
В ходе решения отталкивайтесь от основных математических правил. Например, умножение на ноль всегда дает ноль, а при умножении любого числа на единицу, мы получим в результате исходное число.
Очень часто математические ребусы представляют собой примеры сложения двух чисел. Если при сложении сумма имеет больше знаков нежели слагаемые, значит сумма начинается с "1"
Обращайте внимание на последовательность арифметических действий. Если числовой ребус состоит из нескольких рядов знаков, он может решаться как по вертикали, так и по горизонтали.
Не бойтесь совершать ошибки. Возможно, они подскажут вам верный ход решения. Не пренебрегайте методом перебора. Некоторые ребусы потребуют длительного поэтапного решения, но в итоге вы будете вознаграждены верным ответом и отличной разминкой для вашей сообразительности.
Прежде чем приступить к разгадыванию сложных задач, потренируйтесь на простом примере: ВАГОН+ВАГОН=СОСТАВ. Запишите его в столбик, так будет удобнее решать. Вы имеете два неизвестных пятизначных числа, сумма которых шестизначное число, значит В+В больше 10-ти и С равно 1. Замените символы С на 1.
Сумма А+А – однозначное или двухзначное число с единицей на конце, это возможно в том случае, если сумма Г+Г больше 10 и А равно либо 0, либо 5. Попробуйте предположить, что А равно 0, тогда О равно 5-ти, что не удовлетворяет условиям задачи, т.к. в этом случае В+В=2В не может равняться 15-ти. Следовательно, А=5. Замените все символы А на 5.
Сумма О+О=2О – четное число, может быть равна 5 или 15 лишь в том случае, если сумма Н+Н – двухзначное число, т.е. Н больше 6-ти. Если О+О=5, то О=2. Это решение неверно, т.к. В+В=2В+1, т.е. О должно быть число нечетное. Значит, О равно 7-ми. Замените все О на 7.
Легко заметить, что В равно 8-ми, тогда Н=9. Замените все буквы на найденные числовые значения.
Замените в примере оставшиеся буквы на числа: Г=6 и Т=3. Вы получили верное равенство: 85679+85679=171358. Ребус отгадан.
infourok.ru

Сегодня, уважаемые любители ребусов с цифрами и числами, предлагаю вашему вниманию 10 новых числовых ребусов. На этот раз это будут ребусы с числом 40. Или, говоря по-другому, ребусы с цифрами 4 и 0.
Небольшая подсказка-уточнение: во всех числовых ребусах эти две цифры (4 и 0) будут читаться как единое число-слово - 40 (сорок).
Это будут ребусы с разной степенью сложности. Ребусы с использованием только букв и цифр, а также ребусы, в которых будут присутствовать дополнительные картинки.
Начинаем разгадывание ребусов с самых легких.
Ребус с числом 40 № 1
Ребус с числом 40 № 2

Числовой ребус № 3
Числовой ребус № 4
Числовой ребус № 5
Ребус с числом 40 № 6
Ребус с числом 40 № 7

Ребус с числом 40 № 8
Ребус с числом 40 № 9
Картинку с числовым ребусом № 10 смотрите в самом начале статьи.
Примечание: ответы к ребусам с числом 40 будут напечатаны в конце следующей статьи с ребусами "Детские ребусы про животных".
А вот ответы к предыдущим десяти числовым ребусам с числом 100: стол, пост, постель, росток, настой, восток, рост, строй, рот, подсолнух.
Предлагаю разгадать ребусы и с другими числами (цифрами):Ребусы с цифрой 3
vse-razgadaem.ru