Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
Ячейки Рэлея — Бенара являются одним из трёх стандартных примеров самоорганизации, наряду с лазером и реакцией Белоусова — Жаботинского.
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия из-за возникшей неоднородности плотности. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестеренки)[1]. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
В тонком слое при подогреве снизу образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки[2]. Такая постановка эксперимента исторически была первой, однако здесь на самом деле наблюдается конвекция Марангони, возникающая за счёт действия сил поверхностного натяжения и зависимости их от температуры жидкости.
Важным в задаче о конвекции в плоском слое является тот факт, что для записи её в приближении Буссинеска возможно получить точное аналитическое решение уравнений гидродинамики. Правда, простое точное решение удаётся найти лишь при абстрактной постановке с двумя свободными недеформируемыми границами слоя (как сверху, так и снизу), более реалистичные варианты таких решений не имеют (но для них хорошо работают приближённые аналитические методы, например метод Галёркина).
Приведём здесь решение задачи[3],[4]. Примем, что ось z направлена вверх, перпендикулярно слою, оси x и y параллельны границе. Начало координат удобно выбрать на нижней границе слоя. Исходные уравнения конвекции:
Безразмерная форма уравнений конвекции для малых возмущений равновесия, в предположении экспоненциального роста возмущений во времени (т. н. «Нормальные» возмущения) — :
где — единичный вектор оси z, — соответственно число Прандтля и число Рэлея, — инкремент (скорость роста) возмущений. После обезразмеривания переменная z изменяется от 0 до 1. Т. н. «Нормальные» возмущения являются частными решениями линейной системы дифференциальных уравнений, и поэтому находят широкое применение при исследовании задач в самых различных областях.
Постановка граничных условий производится в предположении, что обе границы недеформируемые, но свободные — при этом отсутствуют касательные напряжения в жидкости. Граничные условия:
, — недеформируемость границ.
, — отсутствие касательных напряжений. Так как считаем, что работаем с жидкостью, для которой справедливо уравнение Навье — Стокса, то можем явно записать вид тензора вязких напряжений и получить граничные условия для компонент скорости.
— закон Навье,
Принимая обозначения для компонент скорости: , перепишем гран.условие для касательных напряжений в терминах скорости:
.
Для возмущений температуры на границе принимается нулевое значение. В итоге, система гран.условий задачи такова:
Теперь, предполагая возмущения нормальными по пространству — (здесь — волновой вектор возмущения, параллельный плоскости ) и заменяя операторы дифференцирования — , можем переписать систему уравнений конвекции в виде системы ОДУ:
Взяв двойной ротор от первого уравнения и спроектировав его на ось z, получим окончательную систему уравнений для возмущений:
Исходя из граничных условий, а также из того, что все производные в системе чётного порядка, удобно представить решение в виде тригонометрических функций:
где n — целое число. Решение в виде синусов удовлетворяет сразу всем граничным условиям.
Далее, обозначая , и подставляя предполагаемый вид решения в уравнения, получим линейную однородную алгебраическую систему для a, b. Из её определителя можно выразить зависимость :
Полагая здесь — граница монотонной устойчивости, невозрастание нормальных возмущений — получим формулу для определения критического числа Рэлея n-ой моды возмущений:
Наименьшее число Рэлея получится при . Минимум зависимости, как несложно убедиться, приходится на , а само минимальное число Рэлея равно . В соответствии с критическим волновым числом в слое возникают структуры в виде валов ширины (в безразмерных единицах).
Для задач с другими вариантами границ критическое число Рэлея оказывается выше. К примеру, для слоя с двумя твёрдыми границами оно равно 1708[5], для слоя с твёрдой верхней и свободной нижней границами — 1156, меняются и критические волновые числа. Однако качественно картина конвективных валов не изменяется.
dic.academic.ru
Важным в задаче о конвекции в плоском слое является тот факт, что для записи её в приближении Буссинеска возможно получить точное аналитическое решение уравнений гидродинамики. Правда, простое точное решение удаётся найти лишь при абстрактной постановке с двумя свободными недеформируемыми границами слоя (как сверху, так и снизу), более реалистичные варианты таких решений не имеют (но для них хорошо работают приближённые аналитические методы, например метод Галёркина).
Приведём здесь решение задачи[3][4]. Примем, что ось z направлена вверх, перпендикулярно слою, оси x и y параллельны границе. Начало координат удобно выбрать на нижней границе слоя. Исходные уравнения конвекции:
∂v→∂t+(v→⋅∇)v→=−1ρ0∇p+νΔv→−βTg→,{\displaystyle {\frac {\partial {\vec {v}}}{\partial t}}+({\vec {v}}\cdot \nabla ){\vec {v}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \Delta {\vec {v}}-\beta T{\vec {g}},}
∂T∂t+v→⋅∇T=χΔT,{\displaystyle {\frac {\partial T}{\partial t}}+{\vec {v}}\cdot \nabla T=\chi \Delta T,}
divv→=0.{\displaystyle \operatorname {div} {\vec {v}}=0.}
Безразмерная форма уравнений конвекции для малых возмущений равновесия, в предположении экспоненциального роста возмущений во времени (т. н. «Нормальные» возмущения) — v→,θ∼eλt{\displaystyle {\vec {v}},\theta \sim e^{\lambda t}} :
λPrv→=−∇p+Δv→+Raθe→z,{\displaystyle {\frac {\lambda }{Pr}}{\vec {v}}=-\nabla p+\Delta {\vec {v}}+Ra\theta {\vec {e}}_{z},}
λθ=Δθ+v→⋅e→z,{\displaystyle \lambda \theta =\Delta \theta +{\vec {v}}\cdot {\vec {e}}_{z},}
divv→=0,{\displaystyle \operatorname {div} {\vec {v}}=0,}
где e→z{\displaystyle {\vec {e}}_{z}} — единичный вектор оси z, Pr,Ra{\displaystyle Pr,Ra} — соответственно число Прандтля и число Рэлея, λ{\displaystyle \lambda } — инкремент (скорость роста) возмущений. После обезразмеривания переменная z изменяется от 0 до 1. Т. н. «Нормальные» возмущения являются частными решениями линейной системы дифференциальных уравнений, и поэтому находят широкое применение при исследовании задач в самых различных областях.
Постановка граничных условий производится в предположении, что обе границы недеформируемые, но свободные — при этом отсутствуют касательные напряжения в жидкости. Граничные условия:
v→⋅e→z=0{\displaystyle {\vec {v}}\cdot {\vec {e}}_{z}=0} , — недеформируемость границ.
σxz=σyz=0{\displaystyle \sigma _{xz}=\sigma _{yz}=0} , — отсутствие касательных напряжений. Так как считаем, что работаем с жидкостью, для которой справедливо уравнение Навье — Стокса, то можем явно записать вид тензора вязких напряжений и получить граничные условия для компонент скорости.
σij=η(∂vi∂xj+∂vj∂xi){\displaystyle \sigma _{ij}=\eta \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}\right)} — закон Навье,
Принимая обозначения для компонент скорости: v→={u,v,w}{\displaystyle {\vec {v}}=\left\{u,v,w\right\}} , перепишем граничное условие для касательных напряжений в терминах скорости:
∂u∂z=0,{\displaystyle {\frac {\partial u}{\partial z}}=0,}
∂v∂z=0{\displaystyle {\frac {\partial v}{\partial z}}=0} .
Для возмущений температуры на границе принимается нулевое значение. В итоге, система граничных условий задачи такова:
z=0,1:{\displaystyle z=0,1:}
w=0;∂u∂z=∂v∂z=0;θ=0{\displaystyle w=0;{\frac {\partial u}{\partial z}}={\frac {\partial v}{\partial z}}=0;\theta =0}
Теперь, предполагая возмущения нормальными по пространству — v→,p,θ∼eλteik→⋅r→{\displaystyle {\vec {v}},p,\theta \sim e^{\lambda t}e^{i{\vec {k}}\cdot {\vec {r}}}} (здесь k→{\displaystyle {\vec {k}}} — волновой вектор возмущения, параллельный плоскости xy{\displaystyle xy} ) и заменяя операторы дифференцирования — Δ=∂2∂z2−k2,∇={ik→;∂∂z}{\displaystyle \Delta ={\frac {\partial ^{2}}{\partial z^{2}}}-k^{2},\nabla =\left\{i{\vec {k}};{\frac {\partial }{\partial z}}\right\}} , можем переписать систему уравнений конвекции в виде системы ОДУ:
λPrv→=−∇p+Δv→+Raθe→z,{\displaystyle {\frac {\lambda }{Pr}}{\vec {v}}=-\nabla p+\Delta {\vec {v}}+Ra\theta {\vec {e}}_{z},}
λθ=Δθ+w,{\displaystyle \lambda \theta =\Delta \theta +w,}
divv→=0.{\displaystyle \operatorname {div} {\vec {v}}=0.}
Взяв двойной ротор от первого уравнения и спроектировав его на ось z, получим окончательную систему уравнений для возмущений:
λPrΔw=Δ2w+k2Raθ,{\displaystyle {\frac {\lambda }{Pr}}\Delta w=\Delta ^{2}w+k^{2}Ra\theta ,}
λθ=Δθ+w.{\displaystyle \lambda \theta =\Delta \theta +w.}
Исходя из граничных условий, а также из того, что все производные в системе чётного порядка, удобно представить решение в виде тригонометрических функций:
w=asinnπz,{\displaystyle w=a\sin n\pi z,}
θ=bsinnπz,{\displaystyle \theta =b\sin n\pi z,}
где n — целое число. Решение в виде синусов удовлетворяет сразу всем граничным условиям.
Далее, обозначая D=n2π2+k2{\displaystyle D=n^{2}\pi ^{2}+k^{2}} , и подставляя предполагаемый вид решения в уравнения, получим линейную однородную алгебраическую систему для a, b. Из её определителя можно выразить зависимость Ra(λ){\displaystyle Ra(\lambda )} :
Ra(λ)=1Prk2(Dλ2+D2(1+Pr)λ+PrD3){\displaystyle Ra(\lambda )={\frac {1}{Prk^{2}}}\left(D\lambda ^{2}+D^{2}(1+Pr)\lambda +PrD^{3}\right)}
Полагая здесь λ=0{\displaystyle \lambda =0} — граница монотонной устойчивости, невозрастание нормальных возмущений — получим формулу для определения критического числа Рэлея n-ой моды возмущений:
Ra∗=(k2+n2π2)3k2.{\displaystyle Ra^{*}={\frac {(k^{2}+n^{2}\pi ^{2})^{3}}{k^{2}}}.}
Наименьшее число Рэлея получится при n=1{\displaystyle n=1} . Минимум зависимости, как несложно убедиться, приходится на k=π2{\displaystyle k={\frac {\pi }{\sqrt {2}}}} , а само минимальное число Рэлея равно Ra∗=274π4≈657{\displaystyle Ra^{*}={\frac {27}{4}}\pi ^{4}\approx 657} . В соответствии с критическим волновым числом в слое возникают структуры в виде валов ширины 2{\displaystyle {\sqrt {2}}} (в безразмерных единицах).
Для задач с другими вариантами границ критическое число Рэлея оказывается выше. К примеру, для слоя с двумя твёрдыми границами оно равно 1708[5], для слоя с твёрдой верхней и свободной нижней границами — 1156, меняются и критические волновые числа. Однако качественно картина конвективных валов не изменяется.
ru-wiki.org
Ячейки Бенара в гравитационном поле.
Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
В качестве жидкости используется, как правило, силиконовое масло.
Ячейки Рэлея — Бенара являются одним из трёх стандартных примеров самоорганизации, наряду с лазером и реакцией Белоусова — Жаботинского.
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестеренки). При определенных граничных условиях и вязкости жидкости образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
Wikimedia Foundation. 2010.
Ячейки Бенара — Механика сплошных сред … Википедия
Ячейки Рэлея-Бенара — Ячейки Бенара в гравитационном поле. Ячейки Бенара или Рэлея Бенара возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом… … Википедия
Ячейка Бенара — Ячейки Бенара в гравитационном поле. Ячейки Бенара или Рэлея Бенара возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом… … Википедия
самоорганизация — Термин самоорганизация Термин на английском self organization Синонимы самосборка Аббревиатуры Связанные термины биомиметические наноматериалы, капсид Определение самопроизвольное образование упорядоченных пространственных или временных структур… … Энциклопедический словарь нанотехнологий
Тороидальный вихрь — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии … Википедия
САМООРГАНИЗАЦИЯ — самопроизвольное (не требующее внеш. организующих воздействий) образование упорядоченных пространственных или временных структур в сильно неравновесных открытых системах (физ., хим., биол. и др.). Непрерывные потоки энергии или в ва, поступающие… … Химическая энциклопедия
Аттрактор Лоренца — решение системы при r=0,3 … Википедия
ДИССИПАТИВНЫЕ СТРУКТУРЫ — устойчивые пространственно неоднородные структуры, возникающие в результате развития неустойчиво стей в однородной неравновесной диссипативной среде. Термин предложен И. Пригожиным. Примеры Д. с. ячейки Бенара (чередование восходящих и нисходящих … Естествознание. Энциклопедический словарь
Конвекция — Течение жидкостей и газа Ползучее течение Ламинарное течение Потенциальное течение Отрыв течения Вихрь Неустойчиво … Википедия
Диссипативная система — (или диссипативная структура, от лат. dissipatio «рассеиваю, разрушаю») это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде… … Википедия
dic.academic.ru
Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
Ячейки Рэлея — Бенара являются одним из трёх стандартных примеров самоорганизации, наряду с лазером и реакцией Белоусова — Жаботинского[источник не указан 1701 день].
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия из-за возникшей неоднородности плотности. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестерёнки)[1]. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
В тонком слое при подогреве снизу образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки[2]. Такая постановка эксперимента исторически была первой, однако здесь на самом деле наблюдается конвекция Марангони, возникающая за счёт действия сил поверхностного натяжения и зависимости их от температуры жидкости.
Важным в задаче о конвекции в плоском слое является тот факт, что для записи её в приближении Буссинеска возможно получить точное аналитическое решение уравнений гидродинамики. Правда, простое точное решение удаётся найти лишь при абстрактной постановке с двумя свободными недеформируемыми границами слоя (как сверху, так и снизу), более реалистичные варианты таких решений не имеют (но для них хорошо работают приближённые аналитические методы, например метод Галёркина).
Приведём здесь решение задачи[3],[4]. Примем, что ось z направлена вверх, перпендикулярно слою, оси x и y параллельны границе. Начало координат удобно выбрать на нижней границе слоя. Исходные уравнения конвекции:
Безразмерная форма уравнений конвекции для малых возмущений равновесия, в предположении экспоненциального роста возмущений во времени (т. н. «Нормальные» возмущения) — 
:
где 
— единичный вектор оси z, 
— соответственно число Прандтля и число Рэлея, 
— инкремент (скорость роста) возмущений. После обезразмеривания переменная z изменяется от 0 до 1. Т. н. «Нормальные» возмущения являются частными решениями линейной системы дифференциальных уравнений, и поэтому находят широкое применение при исследовании задач в самых различных областях.
Постановка граничных условий производится в предположении, что обе границы недеформируемые, но свободные — при этом отсутствуют касательные напряжения в жидкости. Граничные условия:
, — недеформируемость границ.
, — отсутствие касательных напряжений. Так как считаем, что работаем с жидкостью, для которой справедливо уравнение Навье — Стокса, то можем явно записать вид тензора вязких напряжений и получить граничные условия для компонент скорости.
— закон Навье,
Принимая обозначения для компонент скорости: 
, перепишем гран.условие для касательных напряжений в терминах скорости:
.
Для возмущений температуры на границе принимается нулевое значение. В итоге, система гран.условий задачи такова:
Теперь, предполагая возмущения нормальными по пространству — 
(здесь 
— волновой вектор возмущения, параллельный плоскости 
) и заменяя операторы дифференцирования — 
, можем переписать систему уравнений конвекции в виде системы ОДУ:
Взяв двойной ротор от первого уравнения и спроектировав его на ось z, получим окончательную систему уравнений для возмущений:
Исходя из граничных условий, а также из того, что все производные в системе чётного порядка, удобно представить решение в виде тригонометрических функций:
где n — целое число. Решение в виде синусов удовлетворяет сразу всем граничным условиям.
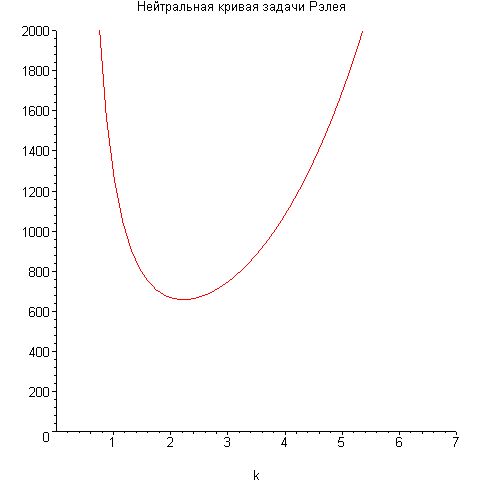
Далее, обозначая 
, и подставляя предполагаемый вид решения в уравнения, получим линейную однородную алгебраическую систему для a, b. Из её определителя можно выразить зависимость 
:
Полагая здесь 
— граница монотонной устойчивости, невозрастание нормальных возмущений — получим формулу для определения критического числа Рэлея n-ой моды возмущений:
Наименьшее число Рэлея получится при 
. Минимум зависимости, как несложно убедиться, приходится на 
, а само минимальное число Рэлея равно 
. В соответствии с критическим волновым числом в слое возникают структуры в виде валов ширины 
(в безразмерных единицах).
Для задач с другими вариантами границ критическое число Рэлея оказывается выше. К примеру, для слоя с двумя твёрдыми границами оно равно 1708[5], для слоя с твёрдой верхней и свободной нижней границами — 1156, меняются и критические волновые числа. Однако качественно картина конвективных валов не изменяется.
wp.wiki-wiki.ru
Ячейки Бенара в гравитационном поле.
Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
В качестве жидкости используется, как правило, силиконовое масло.
Ячейки Рэлея — Бенара являются одним из трёх стандартных примеров самоорганизации, наряду с лазером и реакцией Белоусова — Жаботинского.
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестеренки). При определенных граничных условиях и вязкости жидкости образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
Wikimedia Foundation. 2010.
Ячейка — Ячейка: Ячейка сота Ячейка отсек Ячейка ящик Ячейка бокс, релейный шкаф Депозитарная ячейка сейф в банке, сдаваемый клиентам внаем Ячейка Бенара понятие в физике Ячейка памяти в информатике это часть… … Википедия
Ячейка (значения) — Ячейка (Значения): Ячейка сота Ячейка отсек Ячейка ящик Ячейка бокс, релейный шкаф Депозитарная ячейка сейф в банке, сдаваемый клиентам внаем Ячейка Бенара упорядоченные структуры в жидкости, классический пример самоорганизации в физике Ячейка… … Википедия
Пригожин, Илья Романович — В Википедии есть статьи о других людях с такой фамилией, см. Пригожин. Илья Пригожин Илья Романович Пригожин Дата рождения: 25 января 1917(1917 01 25) Место рождения: Москва … Википедия
И. Р. Пригожин — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Илья Пригожин — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Илья Романович Пригожин — Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Пригожин, Илья — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Пригожин И. — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Пригожин И. Р. — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
Пригожин Илья Романович — Илья Романович Пригожин Дата рождения: 25 января 1917 Место рождения: Москва, Российская империя Дата смерти: 28 мая 2003 Место смерти: Остин … Википедия
dic.academic.ru
Ячейки Бенара в гравитационном поле.
Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
В качестве жидкости используется, как правило, силиконовое масло.
Ячейки Рэлея — Бенара являются одним из трёх стандартных примеров самоорганизации, наряду с лазером и реакцией Белоусова — Жаботинского.
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестеренки). При определенных граничных условиях и вязкости жидкости образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
Wikimedia Foundation. 2010.
Ячейки бенара — в гравитационном поле. Ячейки Бенара или Рэлея Бенара возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то… … Википедия
Ячейки Бенара — Механика сплошных сред … Википедия
Ячейка Бенара — Ячейки Бенара в гравитационном поле. Ячейки Бенара или Рэлея Бенара возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом… … Википедия
Самоорганизация — Самоорганизация процесс упорядочения элементов одного уровня в системе за счёт внутренних факторов, без внешнего специфического воздействия (изменение внешних условий может также быть стимулирующим воздействием). Результат появление единицы … Википедия
Аттрактор Лоренца — решение системы при r=0,3 … Википедия
dic.academic.ru
Ячейки Бенара или Рэлея — Бенара — возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры, то есть равномерно подогреваемой снизу.
Ячейками Бенара можно объяснить происхождение вулканических образований в форме пучка вертикальных колонн — такими являются памятники природы «Девилс-Тауэр» (США) и «Мостовая гигантов» (Северная Ирландия).
Управляющим параметром самоорганизации служит градиент температуры. Вследствие подогрева в первоначально однородном слое жидкости начинается диффузия из-за возникшей неоднородности плотности. При преодолении некоторого критического значения градиента, диффузия не успевает привести к однородному распределению температуры по объёму. Возникают цилиндрические валы, вращающиеся навстречу друг другу (как сцепленные шестерёнки)[1]. При увеличении градиента температуры возникает второй критический переход. Для ускорения диффузии каждый вал распадается на два вала меньшего размера. При дальнейшем увеличении управляющего параметра валы дробятся и в пределе возникает турбулентный хаос, что отчетливо видно на бифуркационной диаграмме или дереве Фейгенбаума.
В тонком слое при подогреве снизу образуются ячейки правильной гексагональной формы, внутри которых жидкость поднимается по центру и опускается по граням ячейки[2]. Такая постановка эксперимента исторически была первой, однако здесь на самом деле наблюдается конвекция Марангони, возникающая за счёт действия сил поверхностного натяжения и зависимости их от температуры жидкости.
Важным в задаче о конвекции в плоском слое является тот факт, что для записи её в приближении Буссинеска возможно получить точное аналитическое решение уравнений гидродинамики. Правда, простое точное решение удаётся найти лишь при абстрактной постановке с двумя свободными недеформируемыми границами слоя (как сверху, так и снизу), более реалистичные варианты таких решений не имеют (но для них хорошо работают приближённые аналитические методы, например метод Галёркина).
Приведём здесь решение задачи[3][4]. Примем, что ось z направлена вверх, перпендикулярно слою, оси x и y параллельны границе. Начало координат удобно выбрать на нижней границе слоя. Исходные уравнения конвекции:
∂v→∂t+(v→⋅∇)v→=−1ρ0∇p+νΔv→−βTg→,{\displaystyle {\frac {\partial {\vec {v}}}{\partial t}}+({\vec {v}}\cdot \nabla ){\vec {v}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \Delta {\vec {v}}-\beta T{\vec {g}},}
∂T∂t+v→⋅∇T=χΔT,{\displaystyle {\frac {\partial T}{\partial t}}+{\vec {v}}\cdot \nabla T=\chi \Delta T,}
divv→=0.{\displaystyle \operatorname {div} {\vec {v}}=0.}
Безразмерная форма уравнений конвекции для малых возмущений равновесия, в предположении экспоненциального роста возмущений во времени (т. н. «Нормальные» возмущения) — v→,θ∼eλt{\displaystyle {\vec {v}},\theta \sim e^{\lambda t}}:
λPrv→=−∇p+Δv→+Raθe→z,{\displaystyle {\frac {\lambda }{Pr}}{\vec {v}}=-\nabla p+\Delta {\vec {v}}+Ra\theta {\vec {e}}_{z},}
λθ=Δθ+v→⋅e→z,{\displaystyle \lambda \theta =\Delta \theta +{\vec {v}}\cdot {\vec {e}}_{z},}
divv→=0,{\displaystyle \operatorname {div} {\vec {v}}=0,}
где e→z{\displaystyle {\vec {e}}_{z}} — единичный вектор оси z, Pr,Ra{\displaystyle Pr,Ra} — соответственно число Прандтля и число Рэлея, λ{\displaystyle \lambda } — инкремент (скорость роста) возмущений. После обезразмеривания переменная z изменяется от 0 до 1. Т. н. «Нормальные» возмущения являются частными решениями линейной системы дифференциальных уравнений, и поэтому находят широкое применение при исследовании задач в самых различных областях.
Постановка граничных условий производится в предположении, что обе границы недеформируемые, но свободные — при этом отсутствуют касательные напряжения в жидкости. Граничные условия:
v→⋅e→z=0{\displaystyle {\vec {v}}\cdot {\vec {e}}_{z}=0}, — недеформируемость границ.
σxz=σyz=0{\displaystyle \sigma _{xz}=\sigma _{yz}=0}, — отсутствие касательных напряжений. Так как считаем, что работаем с жидкостью, для которой справедливо уравнение Навье — Стокса, то можем явно записать вид тензора вязких напряжений и получить граничные условия для компонент скорости.
σij=η(∂vi∂xj+∂vj∂xi){\displaystyle \sigma _{ij}=\eta \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}\right)} — закон Навье,
Принимая обозначения для компонент скорости: v→={u,v,w}{\displaystyle {\vec {v}}=\left\{u,v,w\right\}}, перепишем граничное условие для касательных напряжений в терминах скорости:
∂u∂z=0,{\displaystyle {\frac {\partial u}{\partial z}}=0,}
∂v∂z=0{\displaystyle {\frac {\partial v}{\partial z}}=0}.
Для возмущений температуры на границе принимается нулевое значение. В итоге, система граничных условий задачи такова:
z=0,1:{\displaystyle z=0,1:}
w=0;∂u∂z=∂v∂z=0;θ=0{\displaystyle w=0;{\frac {\partial u}{\partial z}}={\frac {\partial v}{\partial z}}=0;\theta =0}
Теперь, предполагая возмущения нормальными по пространству — v→,p,θ∼eλteik→⋅r→{\displaystyle {\vec {v}},p,\theta \sim e^{\lambda t}e^{i{\vec {k}}\cdot {\vec {r}}}} (здесь k→{\displaystyle {\vec {k}}} — волновой вектор возмущения, параллельный плоскости xy{\displaystyle xy}) и заменяя операторы дифференцирования — Δ=∂2∂z2−k2,∇={ik→;∂∂z}{\displaystyle \Delta ={\frac {\partial ^{2}}{\partial z^{2}}}-k^{2},\nabla =\left\{i{\vec {k}};{\frac {\partial }{\partial z}}\right\}}, можем переписать систему уравнений конвекции в виде системы ОДУ:
λPrv→=−∇p+Δv→+Raθe→z,{\displaystyle {\frac {\lambda }{Pr}}{\vec {v}}=-\nabla p+\Delta {\vec {v}}+Ra\theta {\vec {e}}_{z},}
λθ=Δθ+w,{\displaystyle \lambda \theta =\Delta \theta +w,}
divv→=0.{\displaystyle \operatorname {div} {\vec {v}}=0.}
Взяв двойной ротор от первого уравнения и спроектировав его на ось z, получим окончательную систему уравнений для возмущений:
λPrΔw=Δ2w+k2Raθ,{\displaystyle {\frac {\lambda }{Pr}}\Delta w=\Delta ^{2}w+k^{2}Ra\theta ,}
λθ=Δθ+w.{\displaystyle \lambda \theta =\Delta \theta +w.}
Исходя из граничных условий, а также из того, что все производные в системе чётного порядка, удобно представить решение в виде тригонометрических функций:
w=asinnπz,{\displaystyle w=a\sin n\pi z,}
θ=bsinnπz,{\displaystyle \theta =b\sin n\pi z,}
где n — целое число. Решение в виде синусов удовлетворяет сразу всем граничным условиям.
Далее, обозначая D=n2π2+k2{\displaystyle D=n^{2}\pi ^{2}+k^{2}}, и подставляя предполагаемый вид решения в уравнения, получим линейную однородную алгебраическую систему для a, b. Из её определителя можно выразить зависимость Ra(λ){\displaystyle Ra(\lambda )}:
Ra(λ)=1Prk2(Dλ2+D2(1+Pr)λ+PrD3){\displaystyle Ra(\lambda )={\frac {1}{Prk^{2}}}\left(D\lambda ^{2}+D^{2}(1+Pr)\lambda +PrD^{3}\right)}
Полагая здесь λ=0{\displaystyle \lambda =0} — граница монотонной устойчивости, невозрастание нормальных возмущений — получим формулу для определения критического числа Рэлея n-ой моды возмущений:
Ra∗=(k2+n2π2)3k2.{\displaystyle Ra^{*}={\frac {(k^{2}+n^{2}\pi ^{2})^{3}}{k^{2}}}.}
Наименьшее число Рэлея получится при n=1{\displaystyle n=1}. Минимум зависимости, как несложно убедиться, приходится на k=π2{\displaystyle k={\frac {\pi }{\sqrt {2}}}}, а само минимальное число Рэлея равно Ra∗=274π4≈657{\displaystyle Ra^{*}={\frac {27}{4}}\pi ^{4}\approx 657}. В соответствии с критическим волновым числом в слое возникают структуры в виде валов ширины 2{\displaystyle {\sqrt {2}}} (в безразмерных единицах).
Для задач с другими вариантами границ критическое число Рэлея оказывается выше. К примеру, для слоя с двумя твёрдыми границами оно равно 1708[5], для слоя с твёрдой верхней и свободной нижней границами — 1156, меняются и критические волновые числа. Однако качественно картина конвективных валов не изменяется.
wikiredia.ru
|
|
|
|
|
|
