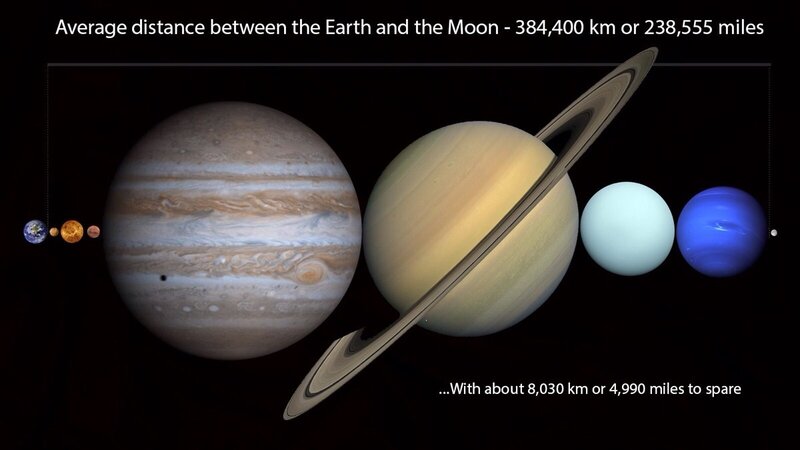
Среднее расстояние от Земли до Луны 384 400 километров. То есть, наш естественный спутник расположился не столь уж далеко. И чтобы продемонстрировать это, специалисты НАСА "затолкали" в имеющийся промежуток оставшиеся планеты Солнечной системы. На удивление, они уместились там почти точно - с небольшими зазорами.
Загадочный парад планет: этот мир придуман не нами...
Можно проверить: Диаметр Меркурия 4879 километров, Венеры - 12104, Марса - 6671, Юпитера - 139822, Сатурна - 116464, Урана -50724, Нептуна - 49244 километра. Плюсуем и получаем 380008 километров. Еще бы и Плутон влез. Но он с 2006 года планетой почему-то уже не считается.
И вот теперь ученые гадают: случайно ли совпадение или так было задумано. Кстати, оно - это совпадение - не единственное. Диаметр Луны подобран так и расположена она на таком расстоянии от Солнца, что оказавшись между ним и Землей, точно прикрывает его диск. Это красивое явление называется солнечным затмением. И мы не могли бы его наблюдать, если бы наш естественный спутник был иным - меньше или больше.
- При всей абсурдности постановки вопроса он не лишен смысла на все 100 процентов, - говорит Джон Бриджес из отделения физики и астрономии Университета Лестера. - Представим себе, что планеты действительно выстроились в ряд между Луной и Землей. Что будет? Юпитер начнет поглощать их. "Всосет" все за неделю. В итоге образуется одна гигантская планета. Подобные обнаружены в других звездных системах - называются Горячие Юпитеры.
В конце останется только один. Один Горячий Юпитер как вдругих звездных системах.
По мнению ученых, у нас катастрофическое слияние планет вроде бы исключено. Но где-то, возможно, оно случалось.
Кстати, ученые прикинули, как бы выглядел небосвод, если бы на месте Луны оказалось бы что-нибудь другое. Изобразили. Вышло потрясающе.
Так выглядел бы Юпитер, если бы встал на место Луны. Тогда бы Земля оказалась бы его спутником.
И все-таки, почему все планеты Солнечной системы укладываются в промежуток между Землей и Луной? Загадка…
www.kp.ru
Молодая Земля сразу же после своего образования была холодным космическим телом, и в ее недрах температура ещё нигде не превышала температуру плавления вещества. Об этом, в частности, свидетельствует полное отсутствие на Земле изверженных (да и любых других) пород старше 4 млрд лет. Об этом же говорят изотопно-свинцовые отношения, показывающие, что процессы дифференциации земного вещества начались значительно позже образования самой Земли и (в противоположность Луне) протекали без существенного плавления. Кроме того, на земной поверхности тогда не было ни океанов, ни атмосферы. Поэтому эффективная механическая добротность Земли в тот ранний период её развития, который в дальнейшем будем называть катархейским, была сравнительно высокой. По сейсмическим данным, в развитой океанической литосфере, т. е. в холодном земном веществе мантийного состава, фактор добротности находится в пределах от 1 000 до 2 000, тогда как в частично расплавленной астеносфере под океанами его значение снижается до 100. В холодной верхней мантии Луны этот фактор приблизительно равен 5 000, а в более прогретой средней мантии снижается до 1 500 (Жарков, 1983).
В отличие от современных условий молодая Земля, как уже отмечалось, была существенно холоднее, лишена астеносферы и ядра, и даже могла характеризоваться отрицательным градиентом температуры в нижней мантии (рис. 29). Поэтому в те далёкие времена механическая добротность Земли в её глубинных недрах скорее всего существенно превышала фактор добротности современной литосферы. Однако следует учитывать, что на приливное взаимодействие планет в основном влияют слои с наименьшими значениями фактора добротности. Учитывая сказанное и для определённости расчётов, примем, что в течение всего катархея, т.е. от момента образования Земли, приблизительно 4,6 млрд лет назад, и вплоть до начала развития в ней геологических процессов в самом начале архея, около 4 млрд. лет назад, значение приливного фактора добротности Земли равнялся 1 500.
Рисунок 29. Температура молодой Земли: 1 и 2 предельные распределения начальной температуры Земли:1 — по В. С. Сафронову (1969) с учётом ударов тел разных размеров, но вначале мелких, а затем и более крупных; 2 — по А. В. Витязеву и др. (1990) с учётом ударов крупных тел в начале процесса аккреции Земли; 3 — принятое распределение начальной температуры Земли, учитывающее как ударное нагревание планеты, так и её приливное разогревание при захвате и разрушении Протолуны.
Приведённая оценка фактора добротности Земли в катархее позволяет определить, что за этот период Луна благодаря приливным взаимодействиям с Землёй оказалась отброшенной от предела Роша (около 17 тыс. км) на расстояние до 160 тыс. км (рис. 26). При этом отодвигание Луны от Земли было неравномерным: вначале очень быстрым, а затем более спокойным.
Рисунок 26. Эволюция расстояния между Луной и Землёй.Интервал I — время развития на Луне анортозитового магматизма; интервал II — время развития базальтового магматизма на Луне (пояснения в тексте).
Количественная модель изменения фактора добротности Земли в остальные периоды геологического времени может быть рассчитана с привлечением эмпирических данных. В частности, средние значения фактора добротности в фанерозое и протерозое могут быть определены по палеонтологическим данным, позволяющим найти для некоторых моментов времени этих эпох число дней в году или, что то же, угловую скорость собственного вращения Земли. Так, по суточной микрослоистости девонских кораллов Дж. Уэллс (1963) показал, что в среднем девоне год состоял приблизительно из 400 сут., а продолжительность суток не превышала 22 ч. В дальнейшем аналогичные определения были выполнены и для других периодов фанерозоя, а также для строматолитов — отложений бактериальных и микроводорослевых плёнок раннего протерозоя (рис. 28).
Рисунок 28. Изменение числа дней в году в связи с эволюцией расстояния между Землёй и Луной.Крестиками показаны эмпирические определения числа дней в году по микрослоистости коралловых построек в фанерозое и строматолитов формации Ганфлинт (2,2 млрд. лет назад) в протерозое (Panella, 1972).
Зная современное расстояние Луны от Земли (384,4 тыс. км), далее удаётся уже рассчитать среднее значение фактора добротности в фанерозое, т.е. за последние 600 млн лет. Оно оказалось приблизительно равным 12. Полученная оценка неплохо совпала с независимым определением приливного фактора добротности Земли около 13, выполненным Г. Макдональдом (1964) на основании обработки данных по современным приливам в океанах и морях. Низкие значения приливного фактора добротности в фанерозое объясняются широким развитием в эту геологическую эпоху мелководных эпиконтинентальных морей, покрывающих сейчас на шельфах около 30% континентальной коры. Но именно в мелководных морях и происходит основное рассеивание энергии приливов за счёт трения приливных течений о дно мелководных бассейнов.
Аналогичным путём по суточной микрослоистости строматолитов в раннем протерозое возрастом около 2,2 млрд лет Г. Паннелла (1972) определил, что тогда в году было 445 сут., а продолжительность самих суток была менее 20 ч (рис. 28). Откуда удаётся определить, что в протерозое фактор приливной добротности Земли равнялся приблизительно 75. Повышенное значение фактора добротности в протерозое вполне понятно, поскольку в ту далёкую эпоху уже образовался глубокий океан, а мелководных эпиконтинентальных морей тогда ещё почти не существовало. Но диссипация приливной энергии в глубоком океане мала, поскольку в этом случае не возникают сильные придонные течения — основная причина приливного торможения Земли.
В архее приливная добротность Земли, как и в фанерозое, должна была быть достаточно низкой по двум причинам. Во-первых, тогда сами океаны ещё были мелкими и в них рассеивалась значительная часть приливной энергии и, во-вторых, в архее уже происходило расплавление верхней мантии (во всяком случае на низких широтах) с существенным её перегревом. Учитывая теперь неразрывность процесса отодвигания Луны от Земли и связывая его воедино в катархее, архее, протерозое и фанерозое, можно определить, что в архее фактор приливной добротности Земли в среднем равнялся 26.
Итак, полученная упрощённая модель изменения фактора добротности Земли Q, основанная на комбинации теоретических соображений с расчётами по эмпирическим данным, выглядит следующим образом: в катархее (от 4,6 до 4,0 млрд лет назад) Q = 1 500; в архее (от 4,0 до 2,6 млрд лет назад) Q = 26; в протерозое (от 2,6 до 0,6 млрд лет назад) Q = 75: в фанерозое (приблизительно от 600 млн лет назад до настоящего времени) Q = 12. Реальное распределение фактора добротности по времени, безусловно, могло меняться по более сложному закону, но основные его черты в приведённом распределении, по-видимому, определены все-таки правильно.
Уточнить приведённую модель возможно, если учесть, что результирующая приливная добротность Земли определяется суммой диссипативных функций мантии и гидросферы, а сами эти функции обратно пропорциональны факторам добротности рассматриваемых геосфер. Кроме того, следует отдельно учитывать приливные диссипативные функции для мантии под океанами (Q ~ 150) и континентами (Q ~ 500), а также для глубоких океанов и мелководных эпиконтинентальных морей, при этом факторы добротности для них можно считать пропорциональными содержащимся в них массам воды. В предыдущих работах (Сорохтин, Ушаков, 1991, 1993) были рассчитаны массы континентальной коры, воды в океанах и средние глубины океанов для всех прошлых геологических эпох. Это позволило нам рассчитать количественную модель зависимости фактора добротности Земли от времени, причём отдельно для гидросферы, мантии и всей Земли в целом. При этом принималось, что в архее и протерозое ещё не существовало мелководных эпиконтинентальных морей, происхождение же архейских мелководных морских бассейнов на океанической коре просто объясняется малыми количествами воды в океанах того времени. Объёмы эпиконтинентальных морей фанерозоя были оценены по палеореконструкциям континентов и площадям распространения морских осадков на континентах.
Построенная по этим условиям уточнённая кривая распределения фактора добротности во времени приведена на рис. 25. Рассчитанная по этой модели зависимость расстояния между центрами тяжести Земли и Луны от времени приведена на рис. 26.
Рисунок 25. Зависимость фактора приливной добротности Земли от времени,построенная с учётом данных по накоплению воды в океанах и по распространению эпиконтинентальных морей в фанерозое
Первое, на что следует обратить внимание в рассматриваемой модели, это совпадение времени эволюции лунной орбиты с возрастом самих планет. Такой вывод сегодня представляется естественным, но не следует забывать, что классические модели приливного взаимодействия Луны с Землёй обычно приводили к слишком короткой продолжительности их нормальной эволюции (около 1,8 млрд лет). Связано это было с тем, что в таких моделях современное низкое значение фактора добротности распространялось на всю историю развития Земли. В результате для выхода из явного противоречия с возрастом образования нашей планетной системы авторам таких гипотез приходилось прибегать к весьма экзотическим представлениям. Так, немецкий учёный Г. Герстенкорн (1955, 1967) считал, что Луна первоначально вращалась в обратном направлении и около 1,8 млрд лет назад подходила к Земле почти на расстояние предела Роша, но затем, после перехода через полярную орбиту, когда её вращение стало прямым, вновь начала удаляться от Земли.
Известный американский геофизик В. Манк (1968) образно описал развитие гипотетического «события Герстенкорна». По его оценкам, в короткий период наибольшего сближения Луны с Землёй океанские приливы должны были достигать высоты 1 км, и каждые 3 ч они обрушивались бы на континенты, приводя к их выравниванию. В это время диссипация (рассеивание) энергии лунных приливов была бы столь высокой, что все земные океаны вскипели бы и испарились, образовав вокруг Земли мощную атмосферу из водяного пара. При этом с учётом парникового эффекта температура у поверхности Земли поднялась бы до 1 000 °С, погубив тем самым любые проявления жизни. К этой страшной картине добавим ещё, что при столь высоких температурах произошла бы почти полная диссоциация (распад) карбонатов — известняков и доломитов с выделением в атмосферу огромных количеств углекислого газа. В результате в земной атмосфере, подобно Венере, возник бы необратимый парниковый эффект с подъёмом приземной температуры до 500-600 °С со всеми вытекающими последствиями.
Безусловно, описываемая катастрофическая ситуация оставила бы свой неизгладимый след в летописи геологической истории Земли, однако таких следов нигде не обнаружено, да и мы живём в комфортабельных климатических условиях, а не в «паровом котле». Это убедительно говорит о том, что «событие Герстенкорна» вовсе не существовало, а начало нормальной эволюции системы Земля-Луна совпадает по времени с моментом их образования как системы двойной планеты около 4,6 млрд лет назад, когда океанов на Земле ещё не существовало.
Рисунок 27. Скорость удаления Луны от Земли, см/год.Масштаб рисунка не позволил привести максимальные значения этой скорости: около 4,6 млрд лет назад она достигала 12×106 см/год, или около 12 км/год, однако уже через 1 млн лет она снизилась до 9,64 м/год, а через 10 млн лет — до 1,37 м/год; в настоящее время Луна отодвигается от Земли со средней скоростью около 3,4 см/год.
Второе обстоятельство, на которое следует обратить внимание, — это неравномерность отодвигания Луны от Земли (рис. 27). С наибольшими скоростями (около 12-10 км/год) Луна отодвигалась от Земли в самом начале своего эволюционного пути (сразу же после разрушения её материнской планеты — Протолуны), около 4,6 млрд лет назад. Однако скорость отодвигания Луны от Земли тогда быстро уменьшалась и уже через 1 млн лет она снизилась до 9,64 м/год, а ещё через 10 млн лет она упала до 1,37 м/год. К концу катархея, около 4 млрд лет назад, скорость удаления Луны от Земли уже не превышала 4,3 см/год. Второй значительный импульс резкого увеличения скорости отодвигания Луны (до 90 см/год) возник на рубеже катархея и архея около 3,9 млрд лет тому назад. Наконец, третий период относительного ускорения отодвигания Луны от Земли, правда, с существенно меньшими скоростями (около 3,4 см/год), приходится на фанерозой. При этом только первый импульс стремительного удаления спутника от планеты был связан с малым исходным расстоянием их образования (напомним, что скорость отодвигания Луны от Земли обратно пропорциональна расстоянию в степени 5,5). Природа же второго и третьего импульсов ускорения была вызвана чисто земными событиями. Архейский пик был связан с началом формирования тогда астеносферы и океанов на Земле, а фанерозойское увеличение скорости отодвигания Луны от Земли — с подъёмом поверхности растущего океана до среднего уровня континентальных шельфов, после чего на континентальной коре возникли многочисленные мелководные эпиконтинентальные моря, в которых и рассеивается основная часть приливной энергии.
Интересно теперь сопоставить полученные результаты с имеющимися эмпирическими данными. Такие данные предоставляет нам палеонтология (о чем уже было сказано выше). Результаты теоретического расчёта эволюции числа дней в году, проведённого по несколько сглаженной модели фактора добротности Q, показаны на рис. 28. На этот же график нанесены все эмпирические данные по определению числа дней в году, полученные на основании изучения микрослоистости кораллов и строматолитов (Шопф, 1982). Как видно из сопоставления теоретической кривой с такими определениями, получено неплохое совпадение теории с экспериментом. Это придаёт уверенность в том, что наши расчёты приводят в основном к верным результатам.
www.gemp.ru
Для проверки возьмем официальные данные NASA - все же, именно у данной организации в настоящий момент наибольший опыт в исследованиях планет Солнечной системы. Итак, согласны приведенным на их сайте данным:
Cредний диаметр Меркурия составляет 4879.4 километра.Средний диаметр Венеры составляет 12103.6 километра.Средний диаметр Марса составляет 6 779 километров.Средний диаметр Юпитера составляет 139 822 километра.Средний диаметр Сатурна составляет 116 464 километраСредний диаметр Урана составляет 50 724 километра.Средний диаметр Нептуна составляет 49 244 километра
Если суммировать: 380 016 километров
Расстояние между Землей и Луной составляет:
В апогее: 363 104 километровВ перигее: 405 696 километров
В среднем: 384 399 километров
А это значит, что если взять среднее расстояние между Землей и Луной, то в него действительно можно всунуть все оставшиеся планеты Солнечной системы. Правда общая цифра оставшегося свободного места будет несколько отличаться от той, что указана на инфографике.
Итак, в итоге у нас останется небольшой запас в 4 383 километра свободного пространства. При большом желании, мы можем втиснуть в него еще и одну или даже две карликовые планеты - например, Эриду, чей диаметр оценивается в 2326 ±12 километров и Макемаке (диаметр 1430±14 километров). Или некогда классифицировавшийся в качестве планеты Плутон (2306 ± 20 километров) и крупнейший из объектов пояса астероидов - 950-километровую Цереру.Разумеется, все эти построения абсолютно умозрительны: мы не учитываем планетарные атмосферы и то, что граница, определяющая где заканчивается атмосфера и начинается поверхость у газовых гигатов достаточно условна. Но все же, на мой взгляд данную картинку вполне можно исполльзовать в качестве доступной демонстрации масштабов Солнечной системы и размеров ее планет.
kiri2ll.livejournal.com
Дарова, писюны. Почитал сегодня немножко про расстояние между Землей и Луной, о чем и поведаю сегодня. "Расстояние между Землей и Луной? Что за херня мужик..." - спросишь ты и будешь прав. И ведь действительно, что тут можно такого интересного рассказать?
Давайте начнем с простых цифр: расстояние между домом и спутником = 384 400 км. Ну вроде не далеко, чуть меньше 1.5 секунды свет идет с Земли до Луны. Визуально она так близко, что можно понюхать её на вкус. Цифры - это, всегда хорошо, но давайте посмотрим на расстояние в реальном масштабе :)
Пока ничего впечатлительно, согласен. Может тогда посмотрим какое количество планеты Земля вместится в это расстояние?
Муахаха, 30 штук! Но да, я вас сюда привел не для этого, сейчас будет самое вкусненькое.
Вы знали, что расстояние настолько большое, что между домом и спутником можно расположить все планеты солнечной системы, ВСЕ СРАНЫЕ ПЛАНЕТЫ ВЛЕЗУТ И ЕЩЕ НА ПОЛ ШЫШЕЧКИ ОСТАНЕТСЯ.
"Пол шышечки" - если быть более точным, это еще 7к км расстояния, туда даже Плутон засунуть можно.
Когда открыли в 1930 году Плутон, гордо заявили о 9й планете солнечной системе. Но до начала 21 века было открыто столько массивных объектов, которые больше Плутона и которые НЕ являются планетами, что он автоматически перестал попадать под определения "планеты", поэтому одни ученые начали его хейтить, другие начали заступаться и говорить, что это свой братюня и его надо считать полноценной планетой. На данный момент это планета, карликовая планета, аля Церера и прочие огрызки.
Ну и вот вам вкусненький постер на тему холивара о Плутоне :)
vadmurzakov.ru
|
|
|
|
|
|
