Ребусы по биологии 7 класс с ответами: Ребусы по биологии

Внеклассное мероприятие «Ребусы по биологии» | Учебно-методический материал по биологии (6 класс):

Опубликовано 26.09.2020 — 6:07 — Нестерова Галина Викторовна

Разработка внеклассного мероприятия

Скачать:

Предварительный просмотр:

Предварительный просмотр:

Муниципальное казенное общеобразовательное учреждение

Купинская специальная (коррекционная) школа-интернат для детей-сирот и детей, оставшихся без попечения родителей с ограниченными возможностями здоровья Новосибирской области

(МКОУ Купинская школа-интернат)

РЕБУСЫ ПО БИОЛОГИИ

Автор-составитель :

 Нестерова Галина Викторовна, учитель биологии.

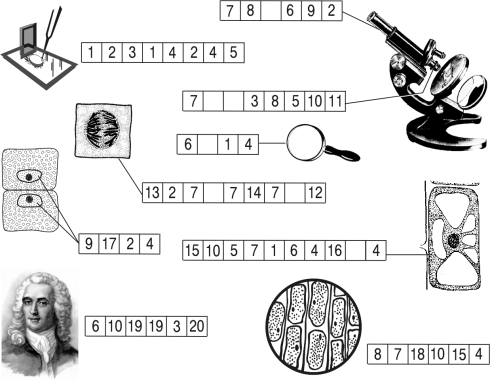
1. … вещества включают белки, жиры, углеводы. 

Слово из 12 букв

2.

3.

4.

5.

6.  

7.

8.

9.

10.

11.Питается только запасами.

12. Оно цветёт и плодоносит. 

13

.

.

14

По теме: методические разработки, презентации и конспекты

Внеклассное мероприятие по биологии «Знатоки биологии»

Игра-викторина по биологии проводится  в 5-7 классах, с целью получения дополнительных знаний по биологии ,а так же для того, чтобы лучше узнать природу, которая нас окружает….

Внеклассное мероприятие по биологии в 6 классе Игра-путешествие по стране «Занимательная биология».

Среди учащихся сформировались две команды. Ребята отправляются в путешествие по стране «Занимательная биология». Они останавливаются на разных станциях и участвуют в  конкурсах. Та команда, котор…

Внеклассное мероприятие по биологии «Абсолютное первенство по биологии 2013»

Внеклассное мероприятие по биологии для обучающихся 9-11 классов разработано таким образом, что позволяет сравнить уровень знаний по предмету учеников разных классов и выявить победителя как в личном …

Игра-путешествие «Занимательная биология» Внеклассное мероприятие по биологии в 6 классе.

Цели и задачи: расширить кругозор знаний учащихся по ботанике, зоологии, экологии; развивать умение логически мыслить; формировать познавательный интерес к биологии, развивать коммуникативность …

Внеклассное мероприятие по биологии «С точки зрения биолога»

Внеклассное мероприятие по биологии для 8-9 классов. Цель:  Развитие логического мышления, памяти, познавательной активности, интереса к предмету биология,  воспитание навыков групповой рабо…

Разработка внеклассного мероприятия по биологии «Турнир знатоки биологии»

Разработка внеклассного мероприятия по биологии  «Турнир знатоки биологии» для обучающихся 7 класса. Задания турнира содержат вопросы по теме «Ракообразные&quot…

Внеклассное мероприятие по биологии «Весёлая биология»

Цель данного мероприятия-  привитие любви к природе, дружеского заинтересованного общения обучающихся….

Поделиться:

Задание 7.

Ребусы — ГДЗ по математике 4 класс Моро Бантова учебник

1 Часть

1234567891010. Проверь себя и оцени свои успехи10. Ребусы11121314151617181920212222. Проверь себя и оцени свои успехи23242526272828. Проверь себя и оцени свои успехи293031323334353636. Проверь себя и оцени свои успехи36. Ребусы37383940414243.. Проверь себя и оцени свои успехи4343. Цепочка4445464748495051525353. Проверь себя и оцени свои успехи54555657585959. Проверь себя и оцени свои успехи606162636465666767. Проверь себя и оцени свои успехи67. Ребус68697071727373. Проверь себя и оцени свои успехи73. Ребус7475767778798080. Проверь себя и оцени свои успехи80. Цепочка8182

083.. Что узнали. Чему научились

123456789101111. Задание на полях1213141515. Вопросы для повторенияРебус8383. Странички для любознательных8485868788899091929393. Проверь себя и оцени свои успехи949596979899.. Проверь себя и оцени свои успехи9999. Задание на полях100101102103104105106106. Проверь себя и оцени свои успехи106. Цепочка107108109110111112113114115116116. Проверь себя и оцени свои успехи117118119120121122123124124. Проверь себя и оцени свои успехи124. Ребус125126127128129130131132133.. Проверь себя и оцени свои успехи133133. Задание на полях134135136137138139140141142142. Проверь себя и оцени свои успехи143144145146147.. Магический квадрат147.. Странички для любознательных147

147. Что узнали. Чему научились

123456789101111. Задание на полях121314151617Цепочка149150150. Ребус151152153154155155. Проверь себя и оцени свои успехи155. Ребус156157158159160161162163164165165. Проверь себя и оцени свои успехи166167168169170171172173174175176177177. Проверь себя и оцени свои успехи179180181182183184185186187188189190.. Проверь себя и оцени свои успехи190190. Задание на полях191192192. Цепочка193194195196197198199199. Проверь себя и оцени свои успехи200201202203204205206207208208. Проверь себя и оцени свои успехи210211212213214215216216. Проверь себя и оцени свои успехи217218219220221222222. Проверь себя и оцени свои успехи224225226227228229230230. Проверь себя и оцени свои успехи231232233234235236237238238. Проверь себя и оцени свои успехи239240241242243244245245. Проверь себя и оцени свои успехи247248249250251252253253. Проверь себя и оцени свои успехи255256257258259.. Ребус259

259. Что узнали. Чему научились

12345678910111213141516171819202122232425262728.. Задание на полях2828. Составляй и решай задачиТест260261262263264265266266. Проверь себя и оцени свои успехи266. Ребус267268269270271272273274275275. Проверь себя и оцени свои успехи276277278279280281282282. Проверь себя и оцени свои успехи282. Ребус283284285286287288289290.. Проверь себя и оцени свои успехи290290. Задание на полях291292293294295295. Проверь себя и оцени свои успехи295. Ребус296297298299300301302303304305305. Проверь себя и оцени свои успехи306307308309310311312… Проверь себя и оцени свои успехи312.. Магический квадрат312312. Задание на полях313314315316317318318. Проверь себя и оцени свои успехи319320321322323324… Ребус324.. Задание на полях324

324. Что узнали. Чему научились

123456789101112…. Задание на полях12… Странички для любознательных12.. Задачи-расчёты1212. Тест13141516171819202121. Цепочка222324252627325326327328329330331332332. Проверь себя и оцени свои успехи333334335336337338339339. Задание339. Проверь себя и оцени свои успехи340341342343344345346347348349349. Ребус350351352353354355356.. Проверь себя и оцени свои успехи356.. Ребус356356. Задание357358359360361362362. Проверь себя и оцени свои успехи363364365366367368369370371371. Проверь себя и оцени свои успехи372373374375.. Проверь себя и оцени свои успехи375375. Задание на полях376377378379379. Проверь себя и оцени свои успехи380381382383384385386387387. Проверь себя и оцени свои успехи387. Ребус388389390391392393394.. Проверь себя и оцени свои успехи394394. Задание395396397398399400401402403403. Проверь себя и оцени свои успехи403. Ребусы404405406407408409410410. Проверь себя и оцени свои успехи410. Ребус411412413414415416417.. Проверь себя и оцени свои успехи417417. Задание на полях418419420421422423424425425. Проверь себя и оцени свои успехи426427428429430431432433434435436

436. Что узнали. Чему научились

123456789101111. Ребус121314151617181920212223242526272829303132333435363738394041424343. Ребус4445464748495050. ТестТексты для контрольных работ

2 Часть

12345677. Ребус891011121313. Проверь себя и оцени свои успехи13. Ребус1415161718192020. Проверь себя и оцени свои успехи21222324252626. Проверь себя и оцени свои успехи272829303132333434. Странички для любознательных353637383939. Проверь себя и оцени свои успехи39. Ребус40414243444546.. Проверь себя и оцени свои успехи4646. Задание4748495051525353. Проверь себя и оцени свои успехи53. Ребус5455565758596060. Проверь себя и оцени свои успехи60. Цепочка6162636464. Проверь себя и оцени свои успехи64. Цепочка6566676869707172…. Проверь себя и оцени свои успехи72.. Задание на полях72.. Странички для любознательных72

072. Что узнали. Чему научились

123456789.. Ребус99. Задание на полях101112131415161718192021222324252627282930313232. Задание на поляхСтранички для любознательных737475767777. Проверь себя и оцени свои успехи77. Ребус7879808182838485868787. Проверь себя и оцени свои успехи87. Ребус8889909192939494. Проверь себя и оцени свои успехи94. Цепочка9596979899100101.. Проверь себя и оцени свои успехи101101. Задание на полях102103104105106107108108. Проверь себя и оцени свои успехи108. Ребус109110111112113113. Проверь себя и оцени свои успехи114115116117118119.. Проверь себя и оцени свои успехи119119. Задание на полях119. Ребус120121122123124.. Проверь себя и оцени свои успехи124124. Магический квадрат125126127128128. Проверь себя и оцени свои успехи128. Ребус129130131132133134135136137138. … Тест138… Наши проекты138.. Магический квадрат138

138. Что узнали. Чему научились

12345678910111212. Задание на полях131415161718192021.. Ребус2121. Задание на полях22232425262728.. Магический квадрат2828. Ребус139140141142143144145145. Проверь себя и оцени свои успехи145. Цепочка146147148149150151152153154155155. Проверь себя и оцени свои успехи157158159160.. Проверь себя и оцени свои успехи160160. Задание на полях161162163164165166167168168. Проверь себя и оцени свои успехи169170171172173173. Проверь себя и оцени свои успехи173. Ребус174175176177178179180181181. Проверь себя и оцени свои успехи181. Ребус182183184.. Проверь себя и оцени свои успехи184184. Задание на полях184. Ребус185186187188189190.. Проверь себя и оцени свои успехи190190. Задание на полях191192193194195196197198199200201202203204… Проверь себя и оцени свои успехи204.. Задания на полях204.. Странички для любознательных204

204. Что узнали. Чему научились

1234567891011. . Занимательная рамка1111. Ребус12131415171819202121. Задание на полях22232425206207208209210.. Проверь себя и оцени свои успехи210210. Цепочка211212213214215216217218.. Проверь себя и оцени свои успехи218218. Магический квадрат219220221222223224225225. Проверь себя и оцени свои успехи225. Ребус226227228229230231.. Проверь себя и оцени свои успехи231.. Цепочка231231. Ребус232233234235236237.. Проверь себя и оцени свои успехи237237. Задание на полях238239240241242243244245246.. Проверь себя и оцени свои успехи246.. Ребус246246. Задание на полях247248249250251252253254255.. Проверь себя и оцени свои успехи255255. Задание на полях256257258259260261262263264264. Проверь себя и оцени свои успехи264. Ребус265266267268269.. Проверь себя и оцени свои успехи269269. Задание на полях270271272273274275276277278

278. Что узнали. Чему научились

12345678910… Странички для любознательных10.. Занимательные рамки1010. Ребус1112131415161717. Ребус1819202122232425279280281282283. . Проверь себя и оцени свои успехи283283. Лабиринт284285286287288289289. Проверь себя и оцени свои успехи289. Цепочка290291292293294295296297298298. Проверь себя и оцени свои успехи298. Цепочка299300301302303304305306307.. Проверь себя и оцени свои успехи307.. Цепочка307307. Задание на полях308309310311312313314315.. Цепочка315315. Ребус316317318319320321322….. Проверь себя и оцени свои успехи322…. Задание на полях322…. Странички для любознательных

322.. Что узнали. Чему научились

1234567899. Ребус1011121314151617.. Задание на полях1717. Ребус1819202122232425262727. Занимательная рамка28293031323334353637322

322. Итоговое повторение всего изученного

1 Нумерация

1234567899. Задание на полях1011121314151617181920212223242526272829

2 Выражения и уравнения

12345678

3 Сложение и вычитание

12345677. Ребусы8910111213141516Магический квадрат

4 Умножение и деление

1234567899. Ребус10111213141516171819

5 Правила о порядке выполнения действий

1234567

6 Величины

1234566. РебусЗадание на полях

7 Геометрические фигуры

123456789101112

8 Задачи

123456788. Ребус910111213141516.. Ребус1616. Магический квадрат1718192021222323. Ребус24252627282930313232. Ребус3334353637383939. Задание на поляхСтранички для любознательных

322. Материал для расширения и углубления знаний

1 Доли2 Единицы площади3 Масштаб. План4 Диагонали прям-ка5 Куб6 Прям. параллелеп.7 Пирамида8 Цилиндр9 ШарТексты для контрольных работ

Средняя оценка 0 / 5. Количество оценок: 0

Оценок пока нет. Поставьте оценку первым.

Научный кроссворд для 7 класса — WordMint

Что такое кроссворд?

Кроссворды публикуются в газетах и ​​других изданиях с 1873 года. Они состоят из сетки квадратов, на которых игрок должен писать слова как по горизонтали, так и по вертикали.

Рядом с кроссвордом будет ряд вопросов или подсказок, которые относятся к различным строкам или строкам клеток в кроссворде. Игрок читает вопрос или подсказку и пытается найти слово, отвечающее на вопрос, состоящее из того же количества букв, что и прямоугольники в соответствующей строке или строке кроссворда.

В некоторых словах используются одни и те же буквы, поэтому они должны совпадать друг с другом. Слова могут различаться по длине и сложности, как и подсказки.

Кому подходит кроссворд?

Самое замечательное в кроссвордах то, что они абсолютно гибкие для любого возраста или уровня чтения, которые вам нужны. Вы можете использовать много слов, чтобы составить сложный кроссворд для взрослых, или всего пару слов для детей помладше.

В кроссвордах можно использовать любое слово, большое или маленькое, поэтому существует буквально бесчисленное количество комбинаций, которые вы можете создать для шаблонов. Шаблон легко настроить в соответствии с возрастом или уровнем обучения ваших учеников.

Как создать шаблон кроссворда?

Для самых простых шаблонов кроссвордов подойдет WordMint!

Готовые шаблоны

Чтобы быстро и легко получить готовый шаблон, просто выполните поиск среди более чем 500 000 существующих шаблонов WordMint. Из такого большого выбора вы обязательно найдете то, что подходит именно вам!

Создайте свою учетную запись с нуля

• Войдите в свою учетную запись (присоединение бесплатно!)
• Перейти к «Моим головоломкам»
• Нажмите «Создать новый пазл» и выберите «Кроссворд».
• Выберите макет, введите название и выбранные подсказки и ответы
• Вот оно! Конструктор шаблонов создаст для вас шаблон кроссворда, и вы сможете сохранить его в своей учетной записи, экспортировать в виде документа Word или PDF и распечатать!

Как выбрать подсказки для кроссворда?

Выбрав тему, выберите подсказки, соответствующие текущему уровню сложности ваших учеников. Для детей младшего возраста это может быть таким же простым вопросом, как «Какого цвета небо?» с ответом «синий».

Полезны ли кроссворды для школьников?

Кроссворды — отличное упражнение для решения задач и познавательных способностей учащихся. Им нужно не только решить подсказку и придумать правильный ответ, но и рассмотреть все остальные слова в кроссворде, чтобы убедиться, что слова сочетаются друг с другом.

Если вы впервые разгадываете кроссворд со своими учениками, вы можете создать для них шаблон часто задаваемых вопросов, чтобы дать им основные инструкции.

Могу ли я распечатать шаблон кроссворда?

Все наши шаблоны можно экспортировать в Microsoft Word для удобной печати или сохранить свою работу в формате PDF для печати для всего класса. Ваши пазлы сохраняются в вашей учетной записи для быстрого доступа и печати в будущем, поэтому вам не нужно беспокоиться о сохранении их на работе или дома!

Могу ли я создавать кроссворды на других языках?

Кроссворды — отличный ресурс для студентов, изучающих иностранный язык, поскольку они одновременно проверяют свои навыки чтения, понимания и письма. При изучении нового языка этот тип теста с использованием нескольких различных навыков отлично подходит для закрепления знаний учащихся.

Мы полностью поддерживаем шаблоны кроссвордов на таких языках, как испанский, французский и японский, с диакритическими знаками, включая более 100 000 изображений, поэтому вы можете создать целый кроссворд на целевом языке, включая все заголовки и подсказки.

Какая у тебя головоломка? | Биология генома

• Редакция
• Открытый доступ
• Опубликовано: 25 августа 2022 г.

• Итай Янаи ¹ и
• Мартин Дж. Лерчер ²  

Биология генома
том 23 , Номер статьи: 179 (2022)
Процитировать эту статью

• 2512 доступов

• 24 Альтметрический

• Детали показателей

Мы не прекратим исследования

И конец всех наших исследований

Прибудет туда, откуда мы начали

И узнаем место в первый раз

– Т. С. Eliot

Природа — это гобелен головоломок, и их решение — главный источник радости в исследованиях. Несмотря на свою сложность, головоломки природы можно классифицировать так же, как головоломки, придуманные людьми для развлечения: головоломки, логические головоломки, головоломки, в которых нам нужно найти связи с явлениями, выходящими за рамки описания задачи, и головоломки, которые требуют от нас нестандартного мышления. , часто путем выявления и отказа от неявных предположений. Эти архетипы можно различать по двум параметрам: относятся ли они к закрытому или открытому миру и требуют ли решения установления связей или более глубокого понимания структуры проблемы. Решение искусственных головоломок может быть важной практикой для развития научного творчества — и это именно то, что программы на получение степени навязывают своим студентам, особенно в области математики, физики и инженерии.

Но природные загадки отличаются от искусственных загадок в одном ключевом аспекте: в разгар продолжающегося исследовательского проекта никогда нельзя быть уверенным в том, какую головоломку ты находишься. То, что ты принимаешь за сложную головоломку, где все вам нужно правильно расположить фигуры перед собой, может на самом деле быть головоломкой, которую вы можете решить, только установив связь с другим полем. Таким образом, в исследовании вы решаете не только саму головоломку, но и соответствующую мета-головоломку: какой тип головоломки вы решаете? Осознание этой иерархической структуры проблемы и переключение между точками зрения, подходящими для разных классов головоломок, может повысить нашу научную креативность, ускоряя наш поиск открытий.

Четыре вида головоломок

Занятие наукой — в отличие от изучения науки — требует творческого решения проблем, которое мы ранее обсуждали как «ночную науку» [1]. Мы решаем проблемы, когда выясняем, какой эксперимент или анализ провести, или когда пытаемся осмыслить наблюдения и данные. Это похоже на решение головоломок, созданных для развлечения, таких как головоломки или головоломки, которые помещают нас в очень похожее ментальное пространство. Такие искусственные головоломки образуют микрокосм решения проблем. Работая над ними, мы испытываем фундаментальную асимметрию: они кажутся очень сложными или даже невозможными, пока мы ищем решение; но когда мы знаем решение, оно кажется почти очевидным.

Головоломки бывают разных видов, каждая из которых имеет свои предпосылки, ограничивающие тип ожидаемого решения. В концептуально простейшем классе головоломок вам представлены все части и возможные типы соединений — все, что вам нужно сделать, это выяснить, как они сочетаются друг с другом. Архетипом этого класса является головоломка, в которой ваши усилия по решению вознаграждаются глобальным образом, возникающим при локальном соединении частей. В качестве примера математической головоломки рассмотрим следующую (также показанную на рис. 1а):

Как получить число 25, объединив все числа 2, 4, 6 и 8 тремя различными операциями из +, −, * и /?

Рис.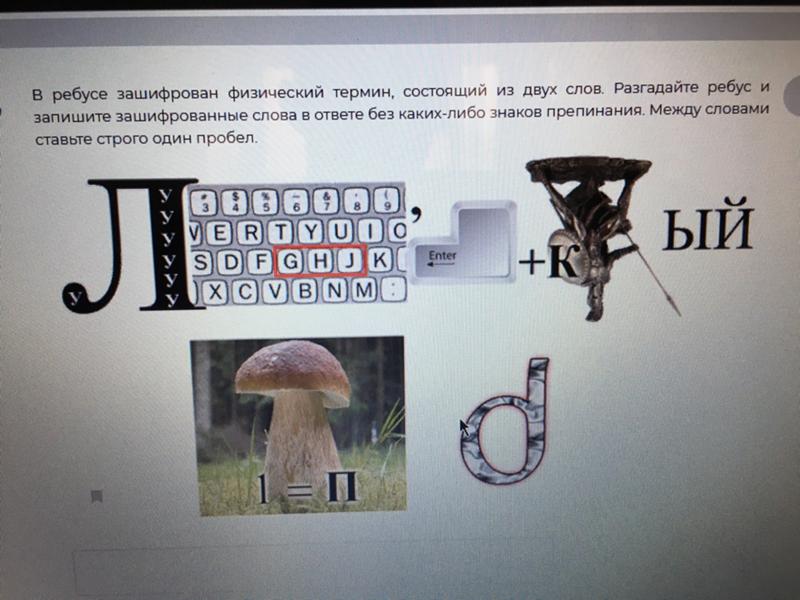 1

Четыре головоломки. a Математическая головоломка (класс I): как сложить каждое из чисел 2, 4, 6 и 8 с тремя различными операциями из +, −, * и /, чтобы получить число 25? b Логическая головоломка (Класс II): Эти весы выводят один из трех символов, соответствующих «левая тяжелее», «равные веса» и «правая тяжелее». Хотя вы можете различать символы, вы не знаете их значения. Найдите четыре взвешивания, позволяющие выделить среди 12 монет ту, которая немного тяжелее или легче остальных. c Головоломка класса III: добавьте отметку, указывающую, что 3 фрикадельки съедены. d Головоломка класса IV: Сможете ли вы соединить точки на линии, имеющей всего 4 прямых ребра?

Изображение в полный размер

Эту головоломку можно решить грубой силой, перепробовав все возможные комбинации — хотя их много. По мере увеличения масштаба таких головоломок растет и их сложность.

Во втором классе головоломок части также четко определены, но для решения требуется логический скачок. Такие «логические головоломки» — часто называемые головоломками — представляют собой четко сформулированную проблему, решение которой часто связано с использованием математических приемов. Например, рассмотрим следующую логическую загадку (рис. 1б):

Представьте, что у вас есть 12 монет, 11 из которых имеют одинаковый вес. Оставшаяся монета либо тяжелее, либо легче остальных. Сможете ли вы найти нечетную монету всего за 4 взвешивания? Вы должны использовать «уникальные» цифровые весы, которые сравнивают два веса. Он выводит один из трех символов, соответствующих следующему: «левый тяжелее», «равные веса» и «правый тяжелее». Вы можете различить три символа, но не знаете их значения.

Хотя найти решение непросто, его общая структура ясна: при первом взвешивании вы ставите n монет слева и n′ других монет справа, и так далее для трех других взвешиваний. Вот и все — никаких уловок вроде сообщения изобретателю весов или плавления монет быть не может. Какова точная логика выбора решения? Если бы мы немедленно предоставили вам решение, оно могло бы показаться простым. Но пытаясь решить ее, вы поймете, что это не так. Что потребуется, так это пролить свет на логическую структуру проблемы — упрощающее понимание, которое делает возможным решение.

Первые два класса головоломок можно рассматривать как головоломки с закрытым миром: составные части решения и их возможные связи известны заранее; задача состоит в том, чтобы собрать их осмысленным образом. Напротив, другие классы головоломок имеют открытый мир. Здесь ответ не заключен в закрытую коробку — вы упускаете важную информацию о компонентах или структуре решения. Следовательно, в третьем классе головоломок вам нужно установить связь с областью, внешней по отношению к формулировке проблемы. Рассмотрим следующее (рис. 1в):

Мужчина готовит девять фрикаделек для своего больного отца. Он отдает их своей дочери, чтобы та отнесла дедушке. Чтобы убедиться, что все фрикадельки прибудут несъеденными, он помечает кастрюлю с фрикадельками римскими цифрами «IX» с помощью несмываемого маркера. По дороге девочка съедает три фрикадельки. Однако маркер у нее есть, и хотя она не может стереть метку своего отца, она может что-то к ней добавить. Что ей сделать, чтобы дедушка не заподозрил неладного?

Вскоре вы поймете, что невозможно получить меньшее число, чем 9, оставаясь в римской системе счисления. Таким образом, эта головоломка требует, чтобы вы связали аспекты, представленные в описании головоломки, с чем-то внешним по отношению к ней. Хотя связь может быть простой, найти ее сложно из-за огромного размера пространства поиска.

Наконец, в четвертом классе головоломок не нужно подключаться к совершенно другому миру, а нужно смотреть нестандартно. Вам нужно более глубокое понимание, которое требует умственного скачка — трюк! Как правило, для этого требуется, чтобы вы сняли ограничение на область поиска, которое не было частью описания проблемы, но которое вы добавили неявно. Рассмотрим головоломку из девяти точек, показанную на рис. 1d, которую вы могли видеть раньше:

Сможете ли вы соединить точки непрерывной линией, состоящей из 4 прямых ребер?

Найти решение с помощью пяти связанных линий довольно просто. Если вы, как и большинство людей, столкнулись с этой проблемой впервые, вы можете неосознанно ограничить свои линии виртуальным прямоугольником, описывающим крайние точки. Мы можем найти решение только тогда, когда отбросим это неявное предположение и позволим себе мыслить нестандартно. Интересно отметить, что решения таких головоломок часто вызывают у нас смех из-за испуга, который мы испытываем, осознавая неожиданный, альтернативный способ увидеть тот же набор фактов.

Эти четыре архетипа головоломок можно расположить на двумерной сетке (Таблица 1). Первое измерение касается полноты формулировки проблемы: закрытый мир (классы I и II) против открытого мира (классы III и IV). Второе измерение касается типа требуемого понимания: поиск связей (классы I и III) и необходимость переформулировать проблему — либо через понимание структуры проблемы (класс II), либо путем выхода за рамки нашего мышления (класс IV). ). Если вы знаете, где вы находитесь в этой сетке, вы знаете, в каком типе головоломки вы находитесь.

Таблица 1. Четыре класса головоломок

Полноразмерная таблица

Исследование как решение головоломок

Глядя на конкретные научные открытия, мы можем видеть, что многие из них идеально подходят к одному из четырех классов головоломок. Все, что требует следования установленному протоколу — например, получение трехмерной структуры белка, сборка полного генома или определение линии эмбриональных клеток организма — является загадкой класса I. Участвующие в этом ученые знают, что решение есть, и они знают, из каких компонентов оно состоит. Ингредиенты «просто» должны быть правильно соединены. Рассмотрим создание атласа типов и состояний клеток с помощью транскриптомики (одноклеточной и пространственной). Для данного органа или всего организма можно собрать численные представления клеток (или частей) для реконструкции системы [2]. Технические препятствия должны быть преодолены, и могут быть открыты новые аспекты, но они ограничены миром, установленным частями.

В качестве примера логической головоломки класса II с закрытым миром рассмотрим, как Крик и его коллеги в годы, последовавшие за открытием двойной спирали, думали о том, какой может быть структура генетического кода [3]. Работая с ограничениями, состоящими в том, что 20 встречающихся в природе аминокислот должны кодироваться всего четырьмя нуклеотидами, они пришли к выводу, что кодирование может выполняться «без запятых»: «Эта статья посвящена математической проблеме, возникшей в связи с синтез белка. Мы приводим решение здесь, потому что оно дает «магическое число» 20, так что наш ответ, возможно, может иметь биологическое значение». Изучая проблему как логическую головоломку, Крик и его коллеги заметили, что набор из 64 триплетов (сегодняшних «кодонов») схлопывается до 20, если добавить ограничение, что должно быть сразу ясно, в каком кадре следует читать код. Четыре однобуквенных кодона («AAA», «CCC», «GGG» и «TTT») исключены, поскольку их использование привело бы к нечеткому кодированию кадра в случае повторов. Остальные 60 триплетов делятся на двадцать групп, каждая из которых содержит три «триплета», являющихся циклическими перестановками друг друга, например «ACG», «CGA» и «GAC». Если использовать только один триплет из каждого набора, а остальных избегать, будет не более 20 пригодных для использования триплетов — точное количество аминокислот. Крик и др. показали, что существует несколько наборов из 20 таких троек, которые действительно делают кадр однозначным. Это прекрасное применение логики, хотя, конечно, это не оказалось правильным решением. Но из него родилась одна очень хорошая идея: они предсказали существование молекулы-адаптера, которая впоследствии оказалась транспортной РНК.

Значительная часть научного прогресса связана с установлением связей, которые составляют головоломки класса III. Например, вслед за другими Гёдель исследовал идею создания полной, свободной от противоречий формальной системы всех математических теорем. Он обнаружил, что, связав этот вопрос с теорией чисел, можно показать существование утверждений, которые нельзя ни доказать, ни опровергнуть в таких формальных системах, тем самым продемонстрировав тщетность популярного в то время поиска единой и полной математической системы [4]. Во втором примере Дарвин лихо связал местные адаптации, которые он видел во время своего кругосветного путешествия на «Бигле», с работами экономиста Мальтуса. Мальтус пессимистично заявлял, что, поскольку неконтролируемый рост населения будет экспоненциальным, войны и болезни должны быть постоянными аспектами человеческого существования. Дарвин понял, что в этой ситуации лучше приспособленные особи имеют больше шансов оставить потомство. Он назвал соответствующий процесс естественным отбором и предположил, что он объясняет, как адаптация в биологических популяциях происходит на протяжении эпох [5].

Однако некоторые из самых удивительных открытий происходят при решении головоломок класса IV. Когда научная проблема кажется неразрешимой, возможно, неправильное предположение — явное или неявное — ограничивает наше пространство поиска. В этих случаях нам нужно мыслить нестандартно. Ярким примером является открытие функции кластеризованных регулярно расположенных коротких палиндромных повторов (CRISPR). В 2000 году Мохика и его коллеги сделали загадочное наблюдение: ранее наблюдаемые наборы коротких геномных повторов, разделенных одинаково короткими спейсерами, не были странной аномалией нескольких изолированных видов, а вместо этого были широко распространены среди прокариот [6]. Как возникли эти повторы? Были ли они эгоистичными элементами какой-то формы или выполняли какие-то полезные для бактерий функции? Последовательности повторов сопротивлялись всем попыткам расшифровать их происхождение или функцию. Так что же было плохим предположением, ограничивающим пространство поиска? Исследователи всего мира отклонили прокладки между повторами, которые, казалось, не имели заметных свойств, как неважные. Как оказалось, спейсеры вместо этого несут функционально важную информацию. Они составляют основу адаптивной системы бактериальной защиты, соответствующей последовательности таких угроз, как вирусы [7].

Наука — это метаголоволомка

Решение проблем глубоко интегрировано в формальную подготовку ученых. Хорошо разработанные курсы бакалавриата ставят перед студентами искусственные задачи, похожие на головоломки. Однако, когда вам предлагают такие образовательные головоломки, вы обычно знаете, в каком классе вы находитесь, точно так же, как вы знаете, когда вам представляют головоломки для развлечения: головоломка — это головоломка, а логическая головоломка — логична, никакие трюки не допускаются. Почти всегда это будут головоломки с закрытым миром, поскольку вопросы упражнений будут основаны на фактах и ​​методах, которые вы узнали в предыдущие недели.

Точно так же, если рассматривать научно-исследовательский проект в ретроспективе, кажется, что он явно вписывается в определенный класс головоломок. Но такая простая классификация основана на ретроспективном взгляде — заниматься наукой в ​​реальном времени — это другое. Когда мы активно работаем над научной проблемой, у нас нет возможности быть уверенным в том, в какой загадке мы находимся, и есть ли у загадки, как мы ее видим, решение. Решение исследовательских головоломок является иерархической задачей. Вам предстоит не только найти решение головоломки, принадлежащей одному из четырех классов. Вы также должны решить мета-головоломку, чтобы узнать, к какому классу головоломки вы относитесь. На языке алгоритмов проблема классификации головоломки образует внешний цикл вокруг самой головоломки. В любой момент головоломка может измениться, заставив вас понять, что вы находитесь в головоломке другого типа, чем вы думали изначально.

Мы приводим два конкретных примера из нашей собственной работы, где мы можем точно определить, когда произошло переключение между классами головоломок. Нас интересовала дупликация генов как механизм создания новых функций, и нам было интересно, какие аспекты могут определять размер генного семейства (таким образом делая это загадкой класса III). Это привело нас к связи с альтернативным сплайсингом: мы рассудили, что новые изоформы могут возникать как в результате дупликации генов, как дополнительные копии генов, так и в результате альтернативного сплайсинга, как дополнительные варианты сплайсинга [8]. Доказательства, подтверждающие эту связь, пришли в виде отрицательной корреляции, которая предполагала, что разные семейства генов, как правило, больше полагаются на тот или иной механизм: семьи с большим количеством копий генов, как правило, имеют меньше изоформ альтернативного сплайсинга на ген, и наоборот. Однако несколько лет спустя мы поняли, что у этой связи была более глубокая причина: были два связанных нестандартных приема, которые изменили то, как мы видели эту связь [9].]. Первый прием заключается в рассмотрении длины гена, которая, как мы обнаружили, коррелирует как с дупликацией генов, так и с альтернативным сплайсингом. Чем длиннее ген, тем больше вероятность того, что он будет генерировать различные варианты сплайсинга, и тем меньше вероятность того, что локальные перестройки генома будут дублировать полную длину гена. Второй трюк связан с уровнем экспрессии гена. Экспрессия, по-видимому, влияет как на дупликацию генов, так и на альтернативный сплайсинг: гены с более высоким уровнем экспрессии с меньшей вероятностью будут продублированы, а также имеют больше вариантов сплайсинга. При контроле этих двух первичных свойств генов корреляция между дупликацией генов и альтернативным сплайсингом исчезает. Нам нужно было переформулировать головоломку с класса III на головоломку класса IV (рис. 2b), чтобы глубже понять природу взаимосвязи между дупликацией генов и альтернативным сплайсингом. Только сместив наше внимание с самих двух процессов на другие свойства генов — думая нестандартно, — мы смогли понять наблюдаемую корреляцию.

Рис. 2

Переключение головоломок в исследовательских проектах. a Схема классов головоломок (см. Таблицу 1). b Переключение классов головоломок в проекте по изучению дупликации генов и альтернативного сплайсинга. c Переключатели в проекте глубокого обучения, направленном на прогнозирование области субстрата ферментов

Изображение в полный размер

Второй пример — это проект, который использует глубокое обучение для прогнозирования области субстрата ферментов [10]. Наша первоначальная идея состояла в том, чтобы просто модифицировать конвейер прогнозирования, который мы разработали ранее для констант Михаэлиса ферментов, К _м [11]. Поэтому мы начали с того, что мы считали типичной задачей класса I. Вскоре после этого мы поняли, что у нас слишком мало отрицательных примеров — субстратов , а не , связанных данным ферментом. Нам пришлось создать случайные отрицательные примеры, но они должны были быть выбраны таким образом, чтобы полученная модель достигла максимальной точности. Эта задача требовала более глубокого понимания структуры проблемы, превращая ее в проблему класса II. Но даже тогда точность предсказаний была относительно низкой. Преобразовав проблему в класс III, мы искали вдохновение в изучении методов обработки естественного языка — источника многих методов ИИ, используемых для решения биологических задач. Мы действительно нашли решение: мы добавили еще один «слой» к существующему числовому представлению [12] аминокислотных последовательностей. Обучив эту модель на наших данных о ферментах, мы могли научить ее выдавать более информативные результаты для наших прогнозов [10].

Интересно, что могут быть типичные шаблоны, согласно которым головоломки меняют классы. Мы сами часто начинаем новый проект с оптимистичным мышлением первого класса, рассматривая его как головоломку. Мы предполагаем, что все компоненты модели и их потенциальные связи просты, и все, что нужно сделать, это собрать их вместе в правильном порядке. Однако чаще всего впоследствии мы обнаруживаем препятствия, которые заставляют нас следовать непредвиденным связям с другими явлениями (класс III), погружаться в более глубокие логические или математические проблемы (класс II) или выявлять неверные предположения, которые мы изначально не подвергали сомнению. (Класс IV).

Незнание загадки, в которой мы находимся, подчеркивает неопределенность, присущую любому исследовательскому проекту. Обратной стороной этой неопределенности является психологическое напряжение, которое она может вызвать. Принятие образа мышления решателя головоломок может помочь нам переосмыслить эту неопределенность — мы можем рассматривать ее как часть игрового процесса, позволяющего нам быть непредвзятыми и не придерживаться жёстко исходной концепции проекта. Без этого игривого отношения к решению головоломок мы можем не только ограничить удовольствие от занятий наукой. Мы также можем упустить немало идей, больших или малых.

История изменений

• 02 сентября 2022 г.

  Ссылка в тексте исправлена.

Литература

1. Янаи И., Лерхер М. Ночная наука. Геном биол. 2019;20:179.

   Артикул

   Google ученый

2. Консорциум Tabula Sapiens, Jones RC, Karkanias J, Krasnow MA, Pisco AO, Quake SR, et al. Tabula Sapiens: многоорганный одноклеточный транскриптомный атлас человека. Наука. 2022;376:eabl4896.

   Артикул

   Google ученый

3. «>

   Крик Ф.Х., Гриффит Дж.С., Оргел Л.Е. Коды без запятых. Proc Natl Acad Sci U S A. 1957; 43:416–21.

   Артикул
   КАС

   Google ученый

4. Гёдель К. Курт Гёдель: собрание сочинений: том I: публикации 1929-1936 гг. Нью-Йорк: издательство Оксфордского университета, США; 1986.

   Google ученый

5. Дарвин С. О происхождении видов путем естественного отбора, или о сохранении привилегированных рас в борьбе за жизнь; 1859.

   Книга

   Google ученый

6. Mojica FJ, Díez-Villaseñor C, Soria E, Juez G. Биологическое значение семейства регулярно расположенных повторов в геномах архей, бактерий и митохондрий. Мол микробиол. 2000; 36: 244–6.

7. Mojica FJM, Díez-Villaseñor C, García-Martínez J, Soria E. Промежуточные последовательности регулярно расположенных прокариотических повторов происходят от чужеродных генетических элементов. Дж Мол Эвол. 2005; 60: 174–82.

   Артикул
   КАС

   Google ученый

8. Копельман Н.М., Ланцет Д., Янаи И. Альтернативный сплайсинг и дупликация генов являются обратно коррелированными эволюционными механизмами. Нат Жене 2005; 37: 588–589. https://doi.org/10.1038/ng1575.

   Артикул
   КАС
   пабмед

   Google ученый

9. Гришкевич В., Янаи И. Длина гена и уровень экспрессии формируют геномные новизны. Геном Res. 2014;24:1497–503.

   Артикул
   КАС

   Google ученый

10. Кролл А., Ранджан С., Энгквист М.К.М., Лерхер М.Дж. Объем субстрата ферментов: общая модель прогнозирования, основанная на машинном и глубоком обучении. нд https://doi.org/10.1101/2022.05.24.493213.

11. Кролл А., Энгквист М.К.М., Хекманн Д., Лерхер М.Дж. Глубокое обучение позволяет прогнозировать константы Михаэлиса в масштабе генома на основе структурных особенностей. PLoS биол. 2021;19:e3001402.

    Артикул
    КАС

    Google ученый

12. Ривз А., Мейер Дж., Серку Т., Гоял С., Лин З., Лю Дж. и др. Биологическая структура и функция возникают в результате масштабирования неконтролируемого обучения до 250 миллионов белковых последовательностей. Proc Natl Acad Sci U S A. 2021; 118. https://doi.org/10.1073/pnas.2016239118.

Ссылки на скачивание

Благодарности

Мы посвящаем эту статью Моше Янаи, любимому разгадывателю головоломок и выдающемуся решателю головоломок. Мы благодарим Далию Баркли и Густаво Франку за их критическое прочтение рукописи.

Информация об авторе

Авторы и организации

1. Институт вычислительной медицины, NYU Langone Health, New York, NY, 10016, USA

   Itai Yanai

2. Институт компьютерных наук Herichine & University Herichine &

   , 40225, Дюссельдорф, Германия

   Martin J. Lercher

Авторы

1. Itai Yanai

   Посмотреть публикации автора

   Вы также можете искать этого автора в
   PubMed Google Академия

2. Martin J. Lercher

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

Contributions

IY и MJL вместе написали рукопись. Авторы прочитали и одобрили окончательный вариант рукописи.

Авторы переписки

Переписка с
Итай Янаи или Мартин Дж. Лерчер.

Декларации этики

Конкурирующие интересы

Авторы заявляют, что у них нет конкурирующих интересов.

Дополнительная информация

Примечание издателя

Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Права и разрешения

Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4. 0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/. Отказ Creative Commons от права на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если иное не указано в кредитной линии данных.