Измерьте время вытекания воды из бутылки физика 7 класс: Измерьте время вытекания воды из бутылки…

Удивительное давление – внеурочная деятельность (конкурсная работа) – Корпорация Российский учебник (издательство Дрофа – Вентана)

Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.

• Участник: Котякина Анна Владиславовна
• Руководитель: Федорова Светлана Ивановна

         Опыты на тему «Удивительное давление»

Опыт 1. Учебник А.В. Перышкин, Физика -7, (Задание после § 40 на стр.118 )

Цель опыта: выяснить, почему вода вытекает из отверстий и проверить гипотезу, что давление жидкости увеличивается с глубиной.

Оборудование: пластиковая бутылка, скотч, вода.

Ход эксперимента: Возьмем пластиковую бутылку. Проколем шилом или толстой нагретой иголкой три отверстия на разной высоте. Заклеим их скотчем. Нальем в бутылку воды и уберем скотч. Вода начнет вытекать из отверстий. Но что мы заметим? Чем ниже расположено отверстие, тем сильнее бьет из нее вода. По мере понижения воды в бутылке дальность вытекания воды уменьшается.

Объяснение эксперимента: Почему же так происходит? На жидкости, как и на все тела, находящиеся на Земле, действует сила тяжести. Поэтому каждый слой жидкости, налитый в сосуд, имеет свой вес. Верхние слои воды давят своим весом на расположенные ниже слои. А ниже лежащие передают давление во все стороны, в том числе и на стенки бутылки. Под действием этого давления вода выливается из бутылки с разным напором струи: чем ниже слой, тем давление жидкости будет больше.

Вывод: Опыт показывает, что внутри жидкости существует давление и на одном уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.

Применение рассматриваемого явления на практике: На глубинах более 1,5 м разность между давлением воды, сжимающим грудную клетку, и давлением воздуха внутри нее возрастает настолько, что у человека уже не хватает сил увеличивать объем грудной клетки при вдохе и наполнять свежим воздухом легкие. Поэтому при погружении более чем на 1,5 м можно дышать только таким воздухом, который сжат до давления, равного давлению воды на этой глубине. Человек при специальной тренировке может без особых предохранительных средств погружаться на глубины до 80 м, давление воды на таких глубинах около 800 кПа. На больших глубинах, если не принять специальных мер защиты, грудная клетка человека может не выдержать давления воды. На глубину до 90 м водолазы могут опускаться под воду, беря с собой запас сжатого воздуха, накачанного в прочные стальные баллоны. Такое снаряжение называют аквалангом. Аквалангом пользуются и спортсмены-пловцы.

На какую глубину может погрузиться человек?

• искатели жемчуга – 30 м.
• рекордное погружение человека без специального оснащения – 124 м. Новозеландский фридайвер Уильям Трабридж установил свой 16 мировой рекорд. Близ Багамских Островов он погрузился на глубину в 124 метра.
• погружение с аквалангом – 143 м. Опытный египетский инструктор по дайвингу и профессиональный технический дайвер Ахмед Габр установил новый мировой рекорд по наибольшей глубине погружения. 18 сентября 2014 г. ему удалось достичь отметки 332,4 метров ниже поверхности воды Красного моря неподалеку от города Дахаб. Чтобы побить предыдущий рекорд, Ахмед должен был опуститься по крайней мере на 330 метров (1083 футов) – именно таким был мировой рекорд француза Паскаля Бернабе, установленный 5 июня 2005 года в Порто-Веккьо. В конце концов, Ахмед Габр благополучно удалось достичь отметки – 332,4 метров (–1 090,5 футов).
• в мягком скафандре – 180 м
• в жестком скафандре – 250 м
• в батискафе – 10 919 м.

Интересные факты

Давление воды в глубинах океана огромно. Если пустую закупоренную бутылку опустить на значительную глубину, затем извлечь вновь, то обнаружится, что давление воды вогнало пробку внутрь бутылки, и она вся будет полна воды. 

Опыт 2. Учебник А.В. Перышкин, Физика -7, (Упр. 16, задание №4 на стр. 111).

Цель опыта: экспериментально доказать справедливость закона Паскаля.

Оборудование: целлофановый пакет, вода, игла.

Ход эксперимента: Возьмем целлофановый пакет, проделаем несколько отверстий. Нальем воды и немного надавим. Напор вытекающих струй увеличится. Причем вода будет вытекать из всех отверстий сразу.

Объяснение эксперимента: Почему же так происходит? Все дело в строении вещества. В отличие от твердых тел отдельные молекулы жидкости могут перемещаться относительно друг друга по всем направлениям. Частицы воды, находящиеся в пакете, уплотняясь при надавливании, передают давление другим слоям жидкости, заполняющей пакет. Таким образом, давление передается в каждую точку жидкости согласно закону Паскаля, который гласит, что давление, производимое на жидкость или газ, передается в любую точку без изменения во всех направлениях.

Применение рассматриваемого явления в жизни и быту: закон Паскаля лежит в основе работы таких устройств как гидравлические прессы, гидравлические подъемники, опрыскиватели, в пневматической системе водоснабжения, водометов, а также в гидравлических тормозах автомашин. При выдавливании краски для волос при окрашивании в парикмахерских используют специальные устройства для того, чтобы выжать краску из тюбика. При надавливании рукой на тюбик краска по закону Паскаля будет передавать давление в разных направлениях, и, если не применять это устройство, то краску полностью не получиться выдавить.

1. гидравлический домкрат

2. Использование действия закона Паскаля для полива огорода

3. гидравлический тормоз

4. Приспособление для выдавливания зубной пасты

Опыт 3.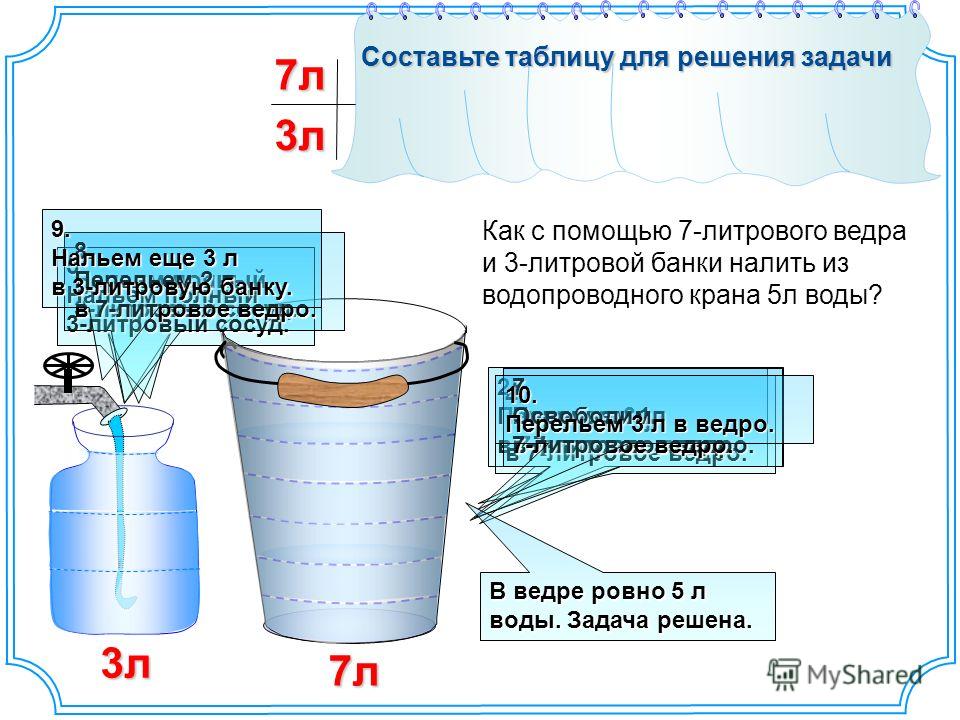 Учебник А.В. Перышкин, Физика -7 (Задание №2 на стр. 125)

Цель опыта: выяснить, почему вода вытекает из отверстий только в том случае, когда крышка в бутылке открыта. В случае, когда бутылка закрыта, вода не вытекает.

Оборудование: пластиковая бутылка, вода

Ход эксперимента: Нальем воду в пластиковую бутылку. Закроем бутылку крышкой. Шилом проткнем отверстие. Что мы видим? Вода не вытекает из бутылки. Когда мы откроем крышку, вода свободно начнет выливаться из бутылки. Можно сделать вывод: вода вытекает из отверстий только в том случае, когда крышка в бутылке открыта. В случае, когда бутылка закрыта, вода не вытекать не будет.

Объяснение опыта: Это происходит потому, что на нее действует только внутреннее давление в бутылке, а оно мало по сравнению с давлением атмосферы снаружи, т.е. мало для того, чтобы вытеснить воду из бутылки. Но как только мы откроем крышку, вода начнет выливаться, так как на воду еще начнет действовать атмосферное давление, а оно уже способно вытолкнуть воду из отверстия. Такое же явление можно наблюдать при работе ливера. Принцип действия, так же как и в предыдущем опыте, основан на действии атмосферного давления. Ливер опускают в воду или любую другую жидкость, Закрывают верхнее отверстие и вынимают из жидкости. Вода не вытекает из ливера. Открываем верхнее отверстие ливера и жидкость выльется. Это происходит потому, что когда мы закрываем пальцем верхнее отверстие, то на столб жидкости, который находится в ливере, действует только внутренне давление, а оно мало, и не способно вытолкнуть жидкость. Открываем верхнее отверстие ливера и жидкость выливает. Это происходит потому, что атмосферное давление сверху на жидкость и давление жидкости, вместе взятые, больше атмосферного давления снизу на жидкость.

Применение рассматриваемого явления на практике и в быту: Данное явление используется в жизни. Зная объяснение данного явления можно изготовить простейшего румойник из пластиковой бутылки. Такой рукомойник можно использовать в походных условиях или на даче. Также это явление лежит в основе работы ливера, который используют для проведения анализов различных жидкостей, в том числе и анализе качества молока.

5. Рукомойник в походных условиях

6. Анализ молока

Ссылка на видео опытов Котякиной Анны https://drive.google.com/drive/u/1/folders/0B21IX7I1ibJmVnZ4MGFKSGxaNWc

Физика. 7 класс ‘Лабораторные работы на дом’

для домашних практических работ

по физике

7 класс

Практическая работа №1.

Задание 1.

Пользуясь масштабной линейкой, измерьте следующие длины предметов и расстояний.

1.длину указательного или среднего пальца ……….

2.длину локтя, т. е. расстояние от конца локтя до конца среднего пальца…………..

3.длину ступни от конца пятки до конца большого пальца………………….

4.окружность шеи………………

5.окружность головы………………..

6.длину…….. ширину…… высоту…… спичечной коробки.

7.длину спички……….. иголки……..

Задание 2.

Ознакомьтесь с рулеткой, осмотрите ее устройство, научитесь разматывать и сматывать рулетку.

1. пользуясь рулеткой, измерьте длину… ширину…….своей комнаты.

2.измерьте высоту……… входной двери.

Задание 3.

Научитесь отмечать при помощи рук и пальцев длины в 1дм. и 1см.

1. возьмите масштабную линейку, отметьте на бумаге карандашом длину 1дм.и раздвинув указательный и средний пальцы, запомните как их нужно раздвигать, чтобы откладывать 1дм. уже без линейки.

2. проверьте длину линии при помощи «собственных» дециметров и при помощи масштабной линейки.

А Б

М К

Сделай вывод.

Практическая работа № 2.

Измерение длины.

Задание1.

1. вечером перед сном, снимите обувь и станьте спиной к косяку раскрытой двери.

2. плотно прикоснитесь к косяку пятками, тазом, спиной и затылком и держите голову прямо.

3. попросите кого-нибудь отметить на косяке небольшую черточку.

4. измерьте расстояние от пола до черточки в сантиметрах и миллиметрах.

5. проделайте тоже самое утром.

6. результаты запишите в таблицу

Вечером

Утром

разница

Задание 2.

Определите среднюю длину своего шага

1. пройдите спокойной и ровной походкой 10 шагов.

3. измерьте пройденное расстояние в метрах и сантиметрах и полученное число разделите

на 10……………………

3. установите среднюю длину своего шага …………….

4. после измерения расстояний шагами обязательно измерьте его рулеткой ………………….

Задание 3.

1. измерьте диаметры монет достоинством 1, 2, 5, 10, 25, 50.копеек

Диаметр монет

1 коп …………..

2 коп…………

5 коп…………

10 коп………….

25 коп………….

50 коп……….

.

Сделай вывод.

Практическая работа № 3.

Измерение диаметров малых тел.

Задание 1.

1.намотайте на цилиндрическую ручку несколько витков проволоки, прижимая как можно туже один виток к другому.

2. измерьте с помощью линейки длину полученного ряда …………….

3.подсчитайте число витков …………….

4. разделите длину полученного ряда на число витков, и вы получите диаметр проволоки ………..

Задание 2.

1.измерьте, диаметры нитей определенного номера как вы делали это в задании № 1.

Нитки № 10 ………………..

№ 30 ………………..

№ 40 ……………….

Задание 3.

1.возмите несколько одинаковых монет, сложите их стопкой и измерьте толщину стопки ——

2. разделите полученный результат на число монет, и вы получите диаметр одной монеты ——

Сделайте вывод

Практическая работа № 4.

Измерение площадей.

Задание 1.

1. возьмите бумагу в клетку и поставьте на него свой ботинок.

2. обведите карандашом края подметки и каблука.

3. посчитайте число полных клеток …………..

4. подсчитайте число не полных клеток ………….

5. площадь опоры ног вычислите так

Задание 2.

1. определите площадь дна чайного стакана, используя тот же прием что и в задании 1.

2. вычисли площадь того же круга по формуле

Задание 3.

1. определи площадь поперечного сечения проводника.

2. сначала определи его диаметр, как это ты делал в п.р. № 3.

3. а затем узнав радиус( это половина диаметра ), вычисли площадь его поперечного сечения ( это площадь круга) по формуле

Сделай вывод.

Практическая работа № 5.

Определение объемов.

Задание 1.

Определите объем спичечной коробки или резинки.

1. измерьте длину……………..мм

2. измерьте ширину…………….мм

3. измерьте высоту………………мм

4. перемножьте полученные числа, и вы получите объем …………………куб. мм.

5. выразите данный объем в………………куб. см. ……………………куб. м.

Задание 2.

Научитесь капать капли.

1. отломите головку от спички, надломите конец палочки, согните ее под углом и положите на край наклоненного стакана, в котором налито немного воды. Вода по спичке будет стекать каплями.

2.подсчитай сколько капель содержится в 50 мл. воды

………………………………………..

3.более совершенную капельницу можно устроить из

трубочки того изолятора, которым покрыт цветной радио провод.

Сняв с провода кусок такой трубочки длиной 20 см, нужно опустить один конец его в стакан с водой, а из другого конца,

предварительно опустив его вниз, отсосать воздух.

5. 4.сравни, как вытекают капли.

Задание 3.

1. подсчитайте, сколько капель воды можно поместить в

чайную ложку до краев……………………..

2. попробуйте теперь на эту воду накапать столько же капель,

сколько их уже поместилось в ложке до краев………………….

Сделайте вывод.

Практическая работа № 6.

Измерение времени.

Задание 1.

1. научитесь быстро находить свой пульс

2. возьмите часы с секундной стрелкой и установите, сколько ударов пульса наблюдается у вас за 1 мин……………………..

3. проделайте обратную работу, считая удары пульса, установите продолжительность одной минуты ( следите за секундной стрелкой)…………………………….

Задание 2.

1. возьмите чистую пол-литровую бутылку, наполните ее водой и, зажав пальцем, горло бутылки, переверните ее вверх дном.

2. отметьте точное время по секундной стрелке часов, отпустите палец и установите, за сколько секунд вытекает вода из бутылки.

………………………………………………………………………….

Задание 3.

Установите продолжительность горения спички.

1. зажгите спичку, одновременно засекая время в секундах. Спичку держите горизонтально.

2. когда спичка будет догорать до конца, помочите пальцы и подержите догорающую спичку за обуглившуюся головку, дав спички догореть до конца.

3. в конце горения отметьте время.

Сделайте вывод.

Практическая работа № 7.

Диффузия.

Задание 1.

1. в тонкостенный стакан с водой с помощью пипетки опустите на дно несколько капель крепкого чая.

2. отметьте через, сколько времени чай окрасит воду во всем стакане ……………………….

3. проверьте наблюдаемое явление , взяв два стакана — с холодной и горячей водой

холодная вода…………………….

горячая вода………………………

Задание 2.

1. возьмите часы с секундной стрелкой, кусок шпагата, линейку ( рулетку ),флакон духов и

встаньте в один коней комнаты.

2.пусть ваш товарищ заметит время и откроет флакон. Вы отметьте время, когда почувст

вуете запах духов. Измерьте расстояние между вами и найдите скорость диффузии.

расстояние

Скорость = ——————— ………………………….м/с

время

Задание 3.

1.налейте в тарелку воды и на ее поверхность капните пипеткой каплю масла. Когда капля

растечется, измерьте диаметр пленки линейкой, положив ее на края тарелки.

…………………………………………

2. вычислите площадь пленки S = ²

Сделайте вывод.

Практическая работа № 8.

Траектория движения.

Задание 1.

Сделайте рисунки, иллюстрирующих приводимые здесь примеры механического движения.

1.мячика, брошенного горизонтально

2.стального шарика, выпушенного из руки

3.снаряда, выпущенного из орудия под углом к горизонту

4.кончика карандаша при письме

5.метеорита

6.полета мухи

7. движение Земли вокруг своей оси

8.движение воды в водопаде

9.движение волчка

10.движение пальцев пианиста

Практическая работа № 9.

Инерция.

Задание 1.

Сделайте иллюстрации, используя приводимые здесь примеры.

1. мальчик сидит на санках. Другой мальчик резко дергает санки за веревку и бежит, но по дороге он спотыкается о кочку.

2. санки, нагруженные ребятами, скатываются с горы и по дороге наезжают на пенек.

3. трамвай резко останавливается. Люди наклоняются.

4. желая стряхнуть ртуть в медицинском термометре, или кляксу с пера ручки, мы делаем

рукой.

4. сделав несколько ударов веслами по воде и подняв весла вверх, мы замечаем, что лодка.

Задание 2.

1. возьмите два железных молотка — один очень маленький,а другой большой.Возьмите также несколько одинаковых орехов.

2. положите орех на что- нибудь твердое и слегка ударьте его большим молотком. Подберите и запомните ту наименьшую высоту, с какой нужно опускать молоток, чтобы разбить орех.

3. теперь возьмите другой орех и опустите на него маленький молоточек с такой же высоты, с какой был опушен большой молоток.

4. опишите что вы наблюдаете

Сделайте вывод.

Практическая работа № 10.

Плотность.

Задание 1.

Рассчитайте среднюю плотность человеческого тела.

1. необходимо знать свою массу………………….кг.

2. объем тела можно определить в ванне

уровень воды до погружения уровень воды после погружения

Заметьте уровень воды до погружения, и после погружения, отметив цветным мелком или клейкой лентой.

3. определите объем воды между этими двумя уровнями, подсчитав, сколько литровых банок воды необходимо вылить в ванну, чтобы вода поднялась от первого уровня до второго.

V = …………………………………………

4. можно сделать иначе, заметить по часам , за сколько времени струя воды из крана наполнит

одну банку и сколько времени эта же струя будет наполнять ванну до отмеченного уровня.

V =………………………………………

5. зная, объем вашего тела и массу, определите его среднюю плотность.

МАССА

ПЛОТНОСТЬ = ————————

ОБЪЕМ

5. по таблице плотностей посмотрите плотность воды и сравните ее c плотностью вашего тела.

Сделайте вывод.

Практическая работа № 11.

Деформация.

Задание 1.

1. возьмите резинку для белья длиной 15 см. и подвесьте на нее груз, масса которого вам известна ………………………кг

2. на сколько растянулась резинка ……………………………см.

Задание 2.

1. положите на два спичечных коробка полоску бумаги

2. затем поочередно кладите монеты, отмечая на сколько

прогибается полоска бумаги

5 коп. на ……………..см.

25 коп на ……………….см.

50 коп на …………………..см.

3. измените форму бумажки, загнув, края и повторите

измерения

5коп на …………………см.

25коп на…………………см.

50кап на…………………см

Сделайте вывод.

Практическая работа № 12.

Трение.

Задание 1.

1. перевяжите книгу ниткой и прикрепите к нитке резинку длиной 20 см.

2. положите книгу на стол и тяните за конец резинки.

3. измерьте длину растянувшейся резинки при равномерном движении книги

L = ……………………см.

4. положите, под книгу две цилиндрические ручки и также тяните за конец резинки

5. измерьте длину растянувшейся резинки при равномерном движении « на катках»

L = ……………………………. см

6. сравните результаты.

Задание 2.

1. измерьте длину растянувшейся резинки при равномерном движении по полированному столу

L = ……………………….. см.

2. положите книгу на шелковую ткань и измерьте длину растянувшейся резинки при

равномерном движении книги.

L = ……………………….

. см.

3. сравните полученные результаты

Сделайте вывод.

Практическая работа № 13.

Простые механизмы.

Задание 1.

1. возьмите большой шуруп ( винт ) и при помощи миллиметровой линейки измерьте длину окружности его головки. Для этого нужно приложить головку винта к делениям миллиметровой линейки.

2. длина окружности головки винта

L = 2 ……………… мм.

3. .возьмите теперь измерительный циркуль и миллиметровую линейку и измерьте расстояние между двумя соседними выступами винтовой нарезки. Это расстояние называется шагом или ходом винта.

H=………………мм.

4. разделите теперь длину окружности головки на шаг винта и узнаете, во сколько раз вы выигрываете в силе, пользуясь этим винтом.

Задание 2.

1. вырежьте из бумаги узкий прямоугольный треугольник и прочертите вдоль ее гипотенузы яркую линию.

2.возмите карандаш и наверните на него этот треугольник, и вы получите модель винта.

Задание 3.

1. возьмите плоскую линейку и положите ее на какой либо трехгранный

брусочек так, чтобы она была в равновесии.

2. отметьте на рычаге-линейке точку опоры рычага.

3. положите на один конец рычага монету 5 коп. а на другой — 1коп.

4. добейтесь равновесия

5. измерьте длины плеч……………………………………………………………………

6. вычислите вес монет……………………………………………………………………

7. проверьте условие равновесия рычага

Формула………………………………………………………………………………………..

Сделайте вывод.

Практическая работа № 14.

Давление.

Задание 1.

1.возьмите целый кирпич с ровными гладкими краями и измерьте

линейкой его длину…………………….см.

ширину…………………..см. 1.

высоту……………………см.

2. определите объем кирпича

V = авh…………..см³

3.подсчитайте площади трех граней кирпича

самой широкой ………………см²

средней боковой………………см²

самой меньшей…………………см²3.

сила давления 2.

4. по формуле давление = ——————————

площадь опоры

подсчитайте давление производимое кирпичом, когда он лежит на широкой грани, когда он стоит на боковой средней грани, и когда он стоит на самой меньшей грани.

Р1……………………Па

Р2…………………….Па

Р3 …………………….Па

Задание 2.

1. приготовьте рисунки примеров того, как человек, уменьшая площадь опоры, увеличивает давление и примеры того , как человек , увеличивая площадь опоры, уменьшает давление.

Сделайте вывод.

Практическая работа № 15.

Воздух и его свойства.

Задание 1.

1. возьмите тонкий упругий прут и как можно быстрее и резче рассекайте им воздух.

2. возьмите широкую фанеру и как можно быстрее ударяйте ею плашмя по воздуху.

3. опишите, что вы наблюдаете при этой работе.

Задание 2

1. Возьмите стакан и медленно опускайте его вверх дном

в высокую стеклянную банку с водой.

2. Во время опускания наблюдайте, что происходит. Отметьте,

на какую часть стакана войдет снизу вода……………………мм

Задание 3

1. сделайте из бумаги воронку, и плотно вставьте ее в горлышко бутылки или пузырька, налейте в нее воды, что вы наблюдаете?

Сделайте вывод

Практическая работа № 16

Закон Паскаля.

Задание 1

1. сверните из тетрадки трубку и перевяжите ее по середине ниткой.

2. прижмите один конец трубки к ладони, а другой конец, вставив трубку в губы, прижмите к лицу.

3. дуньте в трубку с силой воздух (нить должна лопнуть)

4. подсчитайте площадь внутренней поверхности трубки (эта площадь равна приблизительно площади половины станицы тетради)…………………………..см²

5. подсчитайте силу давления, действующую на всю эту площадь, приняв давления на 1 см² , равным приблизительно 0,1 Па…………………………. Н

Сделайте вывод

Задание 2

1. используя энциклопедию, словари и справочники, составьте краткий рассказ на тему : « Гидравлические машины и их применение».

Рассказ должен быть иллюстрирован чертежами и рисунками.

Практическая работа № 17

Давление жидкости.

Задание 1

1. проделайте в стенке пластмассовой бутылке

3 дырочки на разной высоте.

2. налейте в бутылку воды и наблюдайте форму и

направление струи воды, вытекающей их дырочек.

3. во время вытекания воды зажмите большим пальцем горло

бутылки. Что происходит? Почему?…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….

4. прижмите бутылку ко рту и с силой вдувайте в нее воздух. Как будут вытекать струи воды ? ………………………………………………………………………………..

Задание 2

1. возьмите 0,5 л пластмассовую бутылку и отрежьте нижнюю половину бутылки (дно).

2. вырежьте из картона кружочек, соответствующий отрезанному дну.

3. прижмите этот кружочек к нижнему отверстию и придерживая его пальцем опустите эту бутылку в сосуд с водой.

4. отнимите палец от кружка внутри воды. Что происходит? Почему?……………………………………………………………………….………………………………………………………………………………………

5. наливайте в бутылку сверху воду и наблюдайте за кружочком. Что происходит? Почему?………………………………………………………………………………………………………………………………………………………………..

6. вычислите давления жидкости на картонный кружочек по формуле

…………………………………………………………………..Па

Сделайте вывод.

Практическая работа № 18

Сообщающиеся сосуды

Задание 1

1. возьмите 2 стеклянные трубочки или 2 ручки, предварительно вынув из них стержень.

2. соедините их по возможности мягкой эластичной резиновой трубкой.

3. налейте в трубки воды и проверьте справедливость закона сообщающихся сосудов

Задание 2

1. сделайте действующую модель фонтана из воронки, резиновые трубочки и наконечника от аптекарской пипетки.

2. наливайте в воронку воду и наблюдайте высоту и форму струи фонтана при различных положениях трубки и воронки.

Сделайте вывод.

Задание 3

1. заготовьте рисунки и чертежи как очень простых, так и более сложных сообщающихся сосудов, например, рисунки чайника, кофейника, садовой лейки, жидкостного манометра, схему водомерного или нефтемерного стекла, схема водопровода, фонтана.

Практическая работа № 19

Атмосферное давление

Задание 1

1. возьмите стакан, наполните его водой и покройте его бумагой, площадь которого больше площади поперечного стакана.

2. прижмите бумагу к стакану ладонью и переверните стакан вверх дном. Что будите наблюдать? Почему?…………………………………………………………………………………………………

Задание 2

1. сделайте поршневой насос, для этого возьмите трубочку от ручки. На стержень ручки намотайте на один конец плотно нитки, так чтобы получился поршень. Вставьте его в трубочку ручки и опустите в воду.

2. медленно поднимайте поршень вверх и следите за поднимающейся вверх водой.

3. выньте поршень из трубочки и заставьте подниматься волу по ней с помощью рта.

Задание 3

1. сделайте сифон. Для этого возьмите резиновую трубочку со стеклянным наконечником (пипетка) и опустите ее один конец в стакан с водой, так, чтобы другой конец со стеклянным наконечником свешивался в низ.

2. отсосите из трубки воздух, из стеклянного наконечника потечет вода.

3. подставьте, под вытекающую воду другой стакан и когда в нем накопится, немного воды опустите стеклянный наконечник в эту воду и держите оба стакана в таком положении: один стакан выше другого.

4. подумайте, где и когда пользуются сифоном ? ……………………………………………………………………………………………………………………………………………………………………………………………………………………..

Сделайте вывод

Практическая работа № 20.

Закон Архимеда.

Задание 1.

1. сделайте ареометр из пробирки

2. возьмите пробирку и положите в нее столько дроби, чтобы

она держалась в воде вертикально

3. отметьте напильником границу (уровень воды) между подводной и надводной частью пробирки

4. опустите пробирку в масло и отметьте напильником уровень ее погружения

5. опустите теперь пробирку в спирт (или денатурат) и также при помощи напильника

отметьте уровень ее погружения

6. сравните полученные результаты ………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Задание 2

1. возьмите кусочек воска,сделайте из него шарик

2. вложите в него кусочек проволоки и заставьте его плавно затонуть

в стакане с водой

3. подливайте в воду раствора поваренной соли и слегка помешивайте

воду

4. добейтесь сначала того, чтобы шарик держался в равновесии в середине стакана. а затем

того, чтобы он всплыл к поверхности воды

Сделайте вывод

Практическая работа № 21

Плаванье тел

Задание 1

1. возьмите резиновый мяч, кусочек дерева и пустите их плавать в ведре или тазе.

ПРИМЕЧАНИЕ. Хорошо также пустить плавать рыбий пузырь.

2. внимательно наблюдайте над плаванием этих тел и определите на глаз, какая часть этих тел при плавании погружается в воду.

3. запишите результаты……………………………………………………………………………..

………………………………………………………………………………………………………………………………………………………………………………………………………………………….

Задание 2

1. возьмите стакан с раствором поваренной соли и положите на поверхность раствора кусочек парафина и дерева.

2. сравните результаты с заданием 1.

Сделайте вывод

12.1 Расход и его связь со скоростью – College Physics: OpenStax

Глава 12 Динамика жидкости и ее биологические и медицинские приложения

Сводка

• Рассчитать скорость потока.
• Определить единицы объема.
• Опишите несжимаемые жидкости.
• Объясните следствия уравнения неразрывности.

Скорость потока [латекс]\boldsymbol{Q}[/латекс] определяется как объем жидкости, проходящей через некоторое место через область в течение периода времени, как показано на рисунке 1. В символах это может быть пишется как 93}[/латекс]). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рисунок 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P по однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .

Пример 1.

Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь

Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?

Стратегия

Время и скорость потока[latex]\boldsymbol{Q}[/latex] даны, поэтому объем[latex]\boldsymbol{V}[/latex]может быть рассчитан из определения потока оценивать.

Решение 93.} \end{array}[/latex]

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между скоростью потока[латекс]\жирныйсимвол{Q}[/латекс]и скоростью[латекс]\жирныйсимвол{\бар{в}}[/латекс] равно 9.0005

[латекс]\boldsymbol{Q=A\bar{v}},[/латекс]

, где[латекс]\жирныйсимвол{А}[/латекс]– площадь поперечного сечения, а[латекс]\жирныйсимвол{\бар{в}}[/латекс]– средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем

[латекс]\boldsymbol{V=Ad},[/латекс]

, который проходит мимо точки[latex]\textbf{P}[/latex]за время[latex]\boldsymbol{t}.[/latex]Разделив обе части этого соотношения на[latex]\boldsymbol{t}[ /латекс] дает

[латекс]\boldsymbol{\frac{V}{t}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{Ad}{t}}. [/ латекс]

Заметим, что [латекс]\boldsymbol{Q=V/t}[/latex]и средняя скорость равна[латекс]\boldsymbol{v\bar{v}=d/t}.[/latex] Таким образом, уравнение становится [латекс]\boldsymbol{Q=A\bar{v}}.[/латекс]

На рис. 2 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2

[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2.} \end{array}[/latex] [латекс]\rbrace[/латекс]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водоема. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы

Насадка с радиусом 0,250 см присоединена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для сопла. 92}}[/latex][latex]\boldsymbol{=\:1.96\textbf{ м/с}}.[/latex]

Решение для (b)

Мы могли бы повторить это вычисление, чтобы найти скорость в сопле [латекс]\boldsymbol{\bar{v}_2},[/латекс], но мы будем использовать уравнение непрерывности, чтобы дать несколько иное представление. Используя уравнение, в котором указано

[латекс]\boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2},[/latex]

решение для[латекс]\boldsymbol{\bar{v}_2 }[/latex] и подставив [латекс]\boldsymbol{\pi{r}^2}[/latex]вместо площади поперечного сечения, получим 92}}[/latex][latex]\boldsymbol{1,96\textbf{ м/с}=25,5\textbf{ м/с}}. [/latex]

Обсуждение

Скорость 1,96 м/с примерно подходит для воды, вытекающей из шланга без насадок. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид

[латекс]\boldsymbol{n_1A_1\бар{v}_1=n_2A_2\бар{v}_2},[/латекс]

где[latex]\boldsymbol{n_1}[/latex]и[latex]\boldsymbol{n_2}[/latex]количество ответвлений на каждом из участков вдоль трубы.

Пример 3: расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе

Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра составляет[latex]\boldsymbol{8.0\:\mu},[/latex]рассчитайте количество капилляров в системе кровообращения. 92}}[/latex][latex]\boldsymbol{=\:0.27\textbf{ м/с.}}[/latex]

Решение для (b)

Использование[latex]\boldsymbol{n_1A_1\ bar{v}_1=n_2A_2\bar{v}_1},[/latex]присваивая индекс 1 аорте и 2 капиллярам и находя[latex]\boldsymbol{n_2}[/latex](число капилляров) дает[latex]\boldsymbol{n_2=\frac{n_1A_1\bar{v}_1}{A_2\bar{v}_2}}. 93}.[/латекс]

расход

, сокращенно Q , это объем V , протекающий через определенную точку за время t , или Q = V/t

литр

единица объема, равная 10 ⁻³ м ³

Теоретическая и экспериментальная скорость потока жидкости, вытекающей из бутылки с водой с отверстием

Задавать вопрос

спросил
4 года, 8 месяцев назад

Изменено
4 года, 8 месяцев назад

Просмотрено
7к раз

$\begingroup$

Допустим, есть бутылка для воды, наполненная 300 мл воды и имеющая круглое отверстие радиусом 2 мм.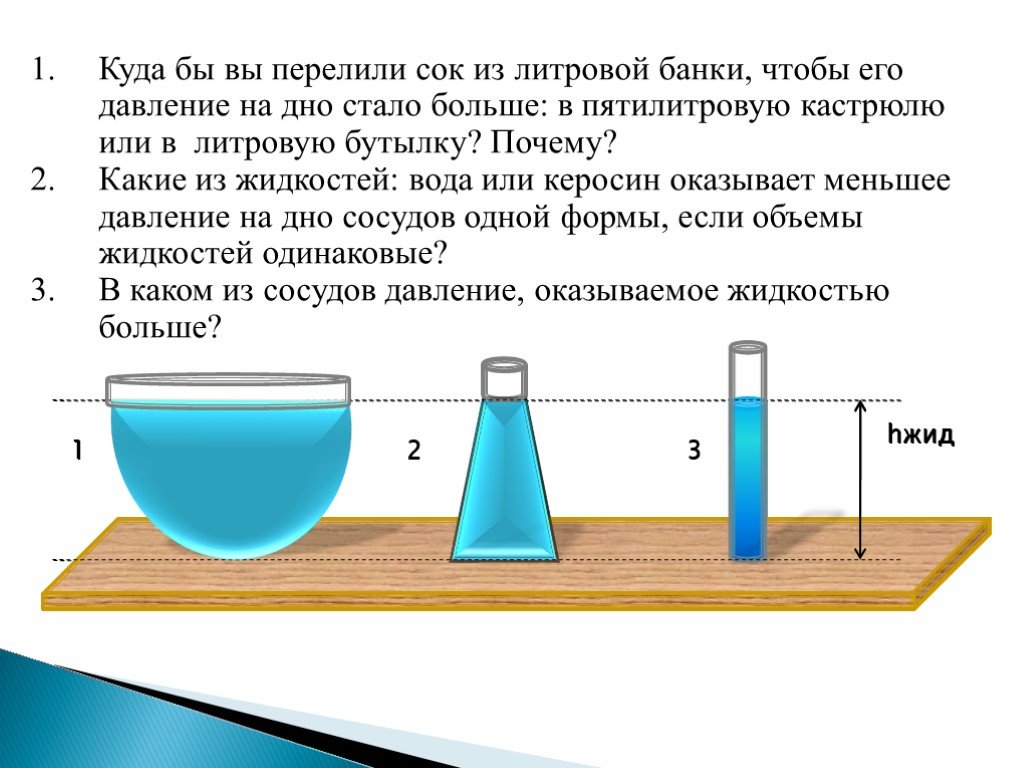 4/8nl, однако я не понимаю, что такое P, поскольку в законе Бернулли давление уравновешивается, и, как упоминалось выше, это не типичный пример трубы.)

В-третьих, я предполагаю, что теоретическая скорость потока все же будет отличаться от экспериментальной скорости потока. Какие факторы вызывают это?

• гидродинамика
• вода
• уравнение Бернулли

$\endgroup$

3

$\begingroup$

У вас две проблемы. Во-первых, закон Бернулли дает мгновенную скорость потока : когда вода выходит из бутылки, высота водяного столба над отверстием также изменяется. Итак, вы сравнили скорость потока при $t=0$ со средней скоростью потока за 5-секундный интервал. Более точное сравнение будет состоять в том, чтобы рассчитать объем воды, потерянной через 5 секунд, и сравнить его с вашими измеренными потерями в 40 мл. Для этого нужно решить дифференциальное уравнение: 92. В этом случае $V_0$ = 251,6 мл, t = 5 с, решение для $V$ = 72 мл со средней скоростью 14 мл/с. По-прежнему не так много улучшений в правильном предсказании 8 мл/с, что подводит меня ко второму пункту:

Думайте об уравнении Бернулли как о лучшем сценарии , аналогичном свободному падению без сопротивления воздуха. Чем дальше вы продвигаетесь от этой идеализации:

1. Вязкой становится ваша жидкость.
2. ваша жидкость становится сжимаемой.
3. Ваш поток жидкости становится неустойчивым.

Я думаю, что пункт № 3 является самым важным фактором для реализации наилучшего сценария. Вы можете попробовать ввести несколько капель пищевого красителя в воду и посмотреть, не заметите ли вы турбулентность вокруг отверстия. Крепление № 3 связано с геометрией вашего контейнера, чтобы его можно было втирать в устойчивый поток, избегая острых краев рядом с потоком жидкости и т. д. прямая трубка (как жидкость, протекающая по медицинскому катетеру).