Содержание
Числовые ребусы презентация, доклад, проект
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Числовые ребусы из раздела Математика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 10 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Числовые ребусы
Числовые ребусы-это примеры, в которых все или некоторые цифры заменены звёздочками или буквами. При этом одинаковые буквы заменяют одинаковые цифры, разные буквы- разные цифры.
У-8
Д-1
А-2
Р-6
Число 8126 является решением этого ребуса:
подробное
решение
Варианты ответов:
В) и-5;р-7; т-6
А) и-5; р-7; т-8
Б) и-6; р-8; т-10
Варианты ответов:
Б) а-8; в-6; д-9
В) а-7; в-3; д-8
А) а-6; в-3; д-8
Варианты правильных ответов
:
А
Б
Б
много
+
ответы
Рассмотрим подробное решение :
Возможны следующие варианты: д=1 д=2
а=2 а=4
р=2
не может быть т. к. по определению, разные буквы обозначают разные цифры
к. по определению, разные буквы обозначают разные цифры
р=2 или р=6
р=2 т.к.а=2
,но
р=6
к=а+а+1, к=5
аналогично находим ,что у=8
8126
8126
16252
+
назад
Ответы к домашнему заданию:
6813+6813=13626 или 6823+6823=13646
495+495=954
85679+85679=171358
До свидания
Скачать презентацию
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.
Для правообладателей
Number Puzzle — Числовые головоломки с ответами
Вопросы-головоломки по математике часто задают на ряде конкурсных экзаменов. Большинство вопросов основаны на арифметических или числовых головоломках. Некоторые из загадок проверяют ваши основы часов, прибыль-убыток, вероятность, время, скорость и расстояние. Вот подборка математических головоломок среднего уровня с ответами. Вы сможете решать концептуальные вопросы в виде алгебраических головоломок. Каждая статья состоит из 10 вопросов.
Большинство вопросов основаны на арифметических или числовых головоломках. Некоторые из загадок проверяют ваши основы часов, прибыль-убыток, вероятность, время, скорость и расстояние. Вот подборка математических головоломок среднего уровня с ответами. Вы сможете решать концептуальные вопросы в виде алгебраических головоломок. Каждая статья состоит из 10 вопросов.
Решите данные вопросы и проверьте свой уровень подготовки:
Q.1. Решите изображение
- 125
- 185
- 156
- 625
Предлагаемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
Очевидно, ( 52-32 )= 16, ( 122-82 )= 80, ( 342-272 )= 427, Таким образом, пропущенное число: ( 212-162 )= 185,. Итак, ответ (б) вариант.
Q.2. Если продавец дает скидку 25%, он все равно получает 25% прибыли. Если он сейчас даст скидку 10%, то какой процент прибыли он получит?
Если он сейчас даст скидку 10%, то какой процент прибыли он получит?
Маркированная цена = 100
Цена после скидки = 75
Прибыль составляет 25%, поэтому Себестоимость = 60
Если они дают скидку 10%, то Цена = 90
Прибыль % = (30/60) x 100 = 50%
Q.3. Четвероногих стульев и четырехногих столов столько же, сколько рабочих в офисе Ямраджа, а трехногих табуреток столько же, сколько четырехногих альмирах. Если количество табуретов на единицу больше, чем количество рабочих, а общее количество ножек равно 585, то каково количество рабочих в офисе?
4 стула на 4 ножках = 4 стола на 4 ножках = количество рабочих.
Табуреты на 3 ножках = almirahs на 4 ножках
Кол-во табуретов = 1 + шт. рабочих
Всего чел. ног = 585, Пусть общее количество рабочих = х.
2x + x × 4 + (x+1) 3 + (x+1) 4 = 585….x = 34.
Таким образом, число рабочих равно 34.
Q.4. Диаграмма представляет собой «магический квадрат», в котором сумма всех строк, столбцов и обеих диагоналей составляет 38. Найти pq
Найти pq
| 2 | 9 | 14 | 13 |
| 15 | |||
| 5 | р | 17 | д |
| 16 |
| 2 | 9 | 14 | 13 |
| 15 | 12 | 3 | 8 |
| 5 | 6 | 17 | 10 |
| 16 | 11 | 4 | 7 |
Итак, ответ 6×10 = 60.
Q.5. В 8:20 утра, на сколько градусов переместилась часовая стрелка часов с полуночи?
После полуночи в 9 часов утра. Движение = 30×8 = 240°. Движение за 20 минут = 20×30/60 = 10° Всего = 240° + 10° = 250°.
В.6. Однажды утром на рассвете один турист начинает подниматься на холм по узкой тропинке, которая спиралью огибает его снизу доверху.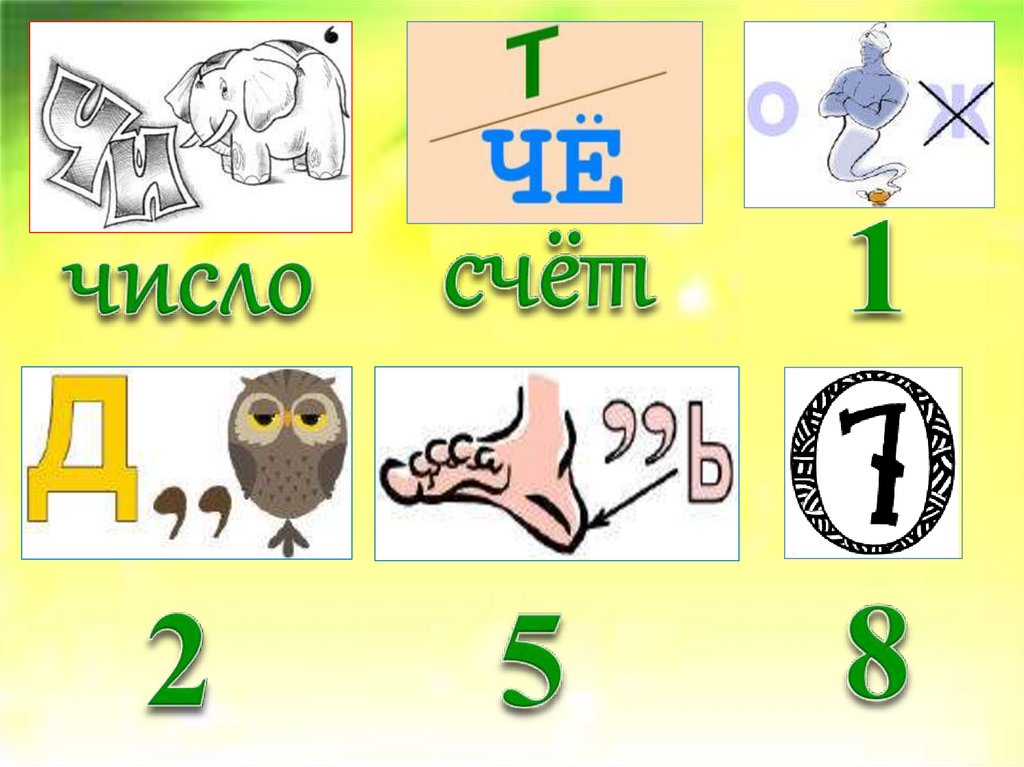 Конечно, он ходит с разной скоростью, делая перерывы, чтобы отдохнуть и пообедать. Вечером он достигает вершины холма, ночует в палатке, а утром начинает спускаться обратно по той же тропе. К закату он достигает подножия холма. Обратите внимание, что его скорость на пути вниз больше, чем его скорость на пути вверх. Докажите, что на пути есть место, которое путешественник займет в обоих походах точно в одно и то же время суток.
Конечно, он ходит с разной скоростью, делая перерывы, чтобы отдохнуть и пообедать. Вечером он достигает вершины холма, ночует в палатке, а утром начинает спускаться обратно по той же тропе. К закату он достигает подножия холма. Обратите внимание, что его скорость на пути вниз больше, чем его скорость на пути вверх. Докажите, что на пути есть место, которое путешественник займет в обоих походах точно в одно и то же время суток.
Представьте себе двух человек, которые одновременно идут по тропинке навстречу друг другу (один с вершины холма, другой снизу). Очевидно, они должны встретиться где-то по пути.
В.7. Что в сетке чисел будет наибольшим: наибольшее из наименьших чисел в каждом столбце или наименьшее из наибольших чисел в каждой строке?
Наименьший из величайших будет больше, чем наибольший из наименьших. Рассмотрим число X, которое находится на пересечении столбца с наибольшим из наименьших (G) и строки с наименьшим из наибольшего (S). Ясно, что S ≥ X ≥ G (равенство будет иметь место, если наименьшее из наибольших совпадает с наибольшим из наименьших). Следовательно, S > T.
Следовательно, S > T.
В.8. Число можно составить из любой даты года, прибавив число месяца к числу дня. Например: 22 ноября станет числом 33, поскольку ноябрь — одиннадцатый месяц, а 22 + 11 = 33. 14 мая станет 19 и так далее. Сколько различных чисел можно составить, используя даты обычного календаря?
Ниже приведен список чисел, которые можно составлять каждый месяц.
января: со 2 по 32 (с 1 января по 31 января)
февраля: с 3 по 30 (с 1 февраля по 28 февраля)
марта: с 4 по 34 марта (с 1 марта по 31 марта)
апреля: с 5 по 34 апреля (с 1 апреля по 30 апреля)
мая: 6 до 36 (с 1 по 31 мая)
июня: с 7 по 36 июня (с 1 по 30 июня)
июля: с 8 по 38 июля (с 1 по 31 июля)
августа: с 9 по 39 (с 1 с августа по 31 августа)
сентября: с 10 по 39 (с 1 по 30 сентября)
октября: с 11 по 41 (с 1 по 31 октября)
Ноябрь: с 12 по 41 (с 1 по 30 ноября)
Декабрь: с 13 по 43 (с 1 по 31 декабря)
Всего возможно 42 номера, каждый номер от 2 до 43 включительно
Q. 9 В казино Анураг делает ставку на число 23 на вращающемся колесе 12 раз и каждый раз проигрывает. На 13-м вращении он делает быстрый подсчет и обнаруживает, что число 17 выпадало три раза за последние 12 вращений, и поэтому он не может решить, ставить ли на 23 или 17 в 13-м вращении. Какое число (23 или 17) даст ему наилучшие шансы на выигрыш и каковы шансы на выигрыш по сделанной им ставке? (Колесо имеет номера от 1 до 36)
9 В казино Анураг делает ставку на число 23 на вращающемся колесе 12 раз и каждый раз проигрывает. На 13-м вращении он делает быстрый подсчет и обнаруживает, что число 17 выпадало три раза за последние 12 вращений, и поэтому он не может решить, ставить ли на 23 или 17 в 13-м вращении. Какое число (23 или 17) даст ему наилучшие шансы на выигрыш и каковы шансы на выигрыш по сделанной им ставке? (Колесо имеет номера от 1 до 36)
- 23; 2:1
- 17; 19:17
- Либо; 18:1
- Либо; 35:1
Так как каждый из спинов является независимым событием, то исход 13-го спина не будет зависеть от исхода предыдущих спинов. Следовательно, шансы на выигрыш числа, на которое ставит Анураг, составляют 35 : 1 в каждом случае.
Q.10. Ленивый экспресс курсирует между P и Q. Как вверх, так и вниз поезд отправляется с начальной станции в 6 утра каждый день и прибывает в пункт назначения в 7 утра через 3 дня. Г-н Джейн однажды путешествовал Ленивым Экспрессом из Q в P. Сколько поездов с таким же названием он пересек по пути?
Сколько поездов с таким же названием он пересек по пути?
Мистер Джайн пересекает ровно семь поездов на маршруте — 3 поезда, которые уже отправились до старта мистера Джейна, и 4 поезда, которые отправились после старта мистера Джейна.
БЕСПЛАТНЫЕ электронные книги
Получите доступ к тщательно подобранным академическими экспертами электронным книгам для сдачи конкурсных экзаменов. Загрузить сейчас
Разместите знаки плюс/минус между цифрами
Начните с последовательности ненулевых цифр 123456789. проблема в том, чтобы поставить плюс или минус
знаки между ними так, что результатом описанной арифметической операции будет 100.
Мы получили один ответ
12 + 3 — 4 + 5 + 67 + 8 + 9 = 100
и предположил, что существует как минимум еще один. Я не утверждаю, что провел исчерпывающий поиск, но
кажется, что есть больше, чем просто два ответа. Один из них
123 + 4 — 5 + 67 — 89 = 100
Я уверен, что там как минимум еще один.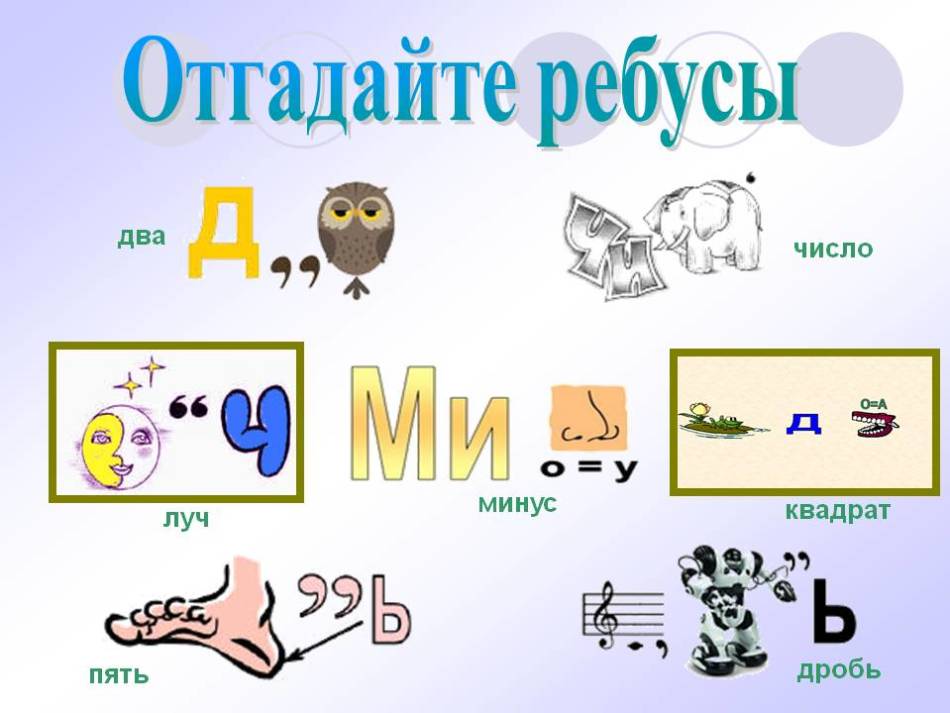 Хотите найти?
Хотите найти?
Есть острое наблюдение, что в двух приведенных выше примерах по крайней мере одна из операций — вычитание. И это также верно для всех добавка (те, в которых разрешены только операции сложения и вычитания) примеры ниже. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять почему, полезно вспомнить понятие цифровых корней.
Вы можете разрешить другие операции, кроме сложения и вычитания. Это приводит к совершенно новому набору проблем с числами, имеющими дробные части. Варианты включают установку целей, отличных от 100. Вот, например, представление единицы, в которой используются все десять цифр:
1 = 148/296 + 35/70
Есть много способов весело провести время, решая арифметические задачи. Один из способов — попытаться представить числа ограниченными средствами. Например, я могу представить 100 пятью тройками как 100 = 33×3 + 3/3. Удивительно, как много чисел можно представить таким образом.
В 1960-х годах очень популярным стал другой вид числовых головоломок. Криптарифмы — это головоломки, полученные
когда цифры в числовых расчетах заменены буквами. Обычно различаются
буквы обозначают разные цифры. Звезды заменяют любую цифру и не связаны друг с другом.
Я получил следующее письмо из Бельгии:
От: Gui et Nicole RULMONT
Дата: Вт, 22 апреля 1997 17:02:44 +0200
Уважаемый Cut-the-Knot,
Английский. Я бельгиец, и меня очень заинтересовал ваш сайт!
Вы писали в «Веселье с цифрами»: Начать с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы расставить между ними знаки плюс или минус так, чтобы результатом описанного арифметического действия было 100.
Несколько лет назад я нашел во французском журнале Science et Vie 11 решений:
1 + 2 + 34 — 5 + 67 — 8 + 9 = 100
12 + 3 — 4 + 5 + 67 + 8 + 9 = 100
123 — 4 — 5 — 6 — 7 + 8 — 9 = 100
123 + 4 — 5 + 67 — 89 = 100
123 + 45 — 67 + 8 — 9 = 100
123 — 45 — 67 + 89 = 100
12 — 3 — 4 + 5 — 6 + 7 + 89 = 100
12 + 3 + 4 + 5 — 6 — 7 + 89 = 100
1 + 23 — 4 + 5 + 6 + 78 — 9 = 100
1 + 23 — 4 + 56 + 7 + 8 + 9 = 100
1 + 2 + 3 — 4 + 5 + 6 + 78 + 9= 100
Если мы поставим «-» перед 1, у нас будет еще одно решение:
-1 + 2-3 + 4 + 5 + 6 + 78 + 9 = 100
Использование «. » десятичное разделение Я нашел другое решение:
» десятичное разделение Я нашел другое решение:
1 + 2,3 — 4 + 5 + 6,7 + 89 = 100 (моё решение)
А как насчет 987654321? Есть 15 решений, сказал Science et Vie :
98 — 76 + 54 + 3 + 21 = 100
9 — 8 + 76 + 54 — 32 + 1 = 100
98 + 7 + 6 — 5 — 4 — 3 + 2 — 1 = 100
98 — 7 — 6 — 5 — 4 + 3 + 21 = 100
9 — 8 + 76 — 5 + 4 + 3 + 21 = 100
98 — 7 + 6 + 5 + 4 — 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 + 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 — 3 + 2 + 1 = 100
98 — 7 + 6 + 5 — 4 + 3 — 2 + 1 = 100
98 — 7 + 6 — 5 + 4 + 3 + 2 — 1 = 100
98 + 7 — 6 — 5 + 4 + 3 — 2 + 1 = 100
98 — 7 — 6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 — 3 + 2 — 1 = 100
9 + 8 + 76 + 5 — 4 + 3 + 2 + 1 = 100
9 — 8 + 7 + 65 — 4 + 32 — 1 = 100
Напишите знак «-«, три решения:
-9 + 8 + 76 + 5-4 + 3 + 21 = 100
-9 + 8 + 7 + 65 — 4 + 32 + 1 = 100
-9-8 + 76 — 5 + 43 + 2 + 1 = 100
С десятичной точкой:>
9 + 87,6 + 5,4 — 3 + 2 — 1 = 100 (моё решение)
Если «перетасовать» цифры, то есть много решений.
