Содержание
10 увлекательных задач от советского математика
12 сентября 2021Отдых
Попробуйте решить головоломки от популяризатора математики Бориса Кордемского, не пользуясь подсказками.
Поделиться
0
1. Переправа через реку
Небольшой воинский отряд подошёл к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Каким образом?
Показать ответ
Скрыть ответ
2. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить ещё одну заготовку. Сколько деталей можно сделать таким образом из тридцати шести свинцовых заготовок?
Показать ответ
Скрыть ответ
3.
Во время прилива
Недалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы десять ступенек; расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды.
Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через какое время покроется водой третья ступенька верёвочной лесенки?
Показать ответ
Скрыть ответ
4. Девяносто девять
Сколько нужно поставить знаков «плюс» (+) между цифрами числа 987 654 321, чтобы в сумме получилось 99?
Показать ответ
Скрыть ответ
5. Для Цимлянского гидроузла
В выполнении срочного заказа по изготовлению измерительных приборов для Цимлянского гидроузла приняла участие бригада в составе опытного бригадира и девяти молодых рабочих.
В течение дня каждый из юных рабочих смонтировал по 15 приборов, а бригадир — на 9 приборов больше, чем в среднем каждый из десяти членов бригады. Сколько всего измерительных приборов было смонтировано бригадой за один рабочий день?
Показать ответ
Скрыть ответ
6.
Попробуйте отвесить
В пакете находится 9 кг крупы. Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Показать ответ
Скрыть ответ
7. Смышлёный малыш
Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:
— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.
Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну.
Сколько же лет было малышу и каждому из остальных братьев?
Показать ответ
Скрыть ответ
8. Раздробить на части
Раздробите 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвёртую разделить на 2, то все результаты будут равными. Сумеете сделать?
Показать ответ
Скрыть ответ
9. Посадка деревьев
Пятиклассникам и шестиклассникам было поручено посадить деревья по обе стороны улицы по равному количеству на каждой стороне.
Чтобы не ударить лицом в грязь перед шестиклассниками, пятиклассники вышли на работу пораньше и успели посадить 5 деревьев, пока пришли старшие ребята, но оказалось, что они сажали деревья не на своей стороне.
Пришлось пятиклассникам идти на свою сторону и вновь начинать работу. Шестиклассники, конечно, справились с задачей раньше. Тогда учитель предложил:
— Пойдём, ребята, поможем пятиклассникам!
Все согласились. Перешли на другую сторону улицы, посадили 5 деревьев, отдали, значит, долг, да ещё успели посадить 5 деревьев, и вся работа была закончена.
— Хоть вы пришли раньше нас, а всё-таки мы вас обогнали, — посмеялся один шестиклассник, обращаясь к младшим ребятам.
— Подумаешь, обогнали! На 5 деревьев только, — возразил кто-то.
— Нет, не на 5, а на 10, — зашумели шестиклассники.
Спор разгорался. Одни настаивают на том, что на 5, другие пытаются как-то доказать, что на 10. Кто же прав?
Показать ответ
Скрыть ответ
10. Четыре теплохода
В порту пришвартовались 4 теплохода. В полдень 2 января они одновременно покинули порт. Известно, что первый теплоход возвращается в этот порт через каждые 4 недели, второй — через каждые 8 недель, третий — через 12 недель, а четвёртый — через 16 недель.
Когда в первый раз теплоходы снова сойдутся все вместе в этом порту?
Показать ответ
Скрыть ответ
Задачи для этой подборки взяты из сборника «Математическая смекалка» Бориса Кордемского, который выходил в издательстве «Альпина Паблишер».
Читайте также 🔥
- 15 занимательных задач для тренировки ума и сообразительности
- 11 хитрых советских головоломок для проверки логики и сообразительности
- 5 задач, которые предлагают решить на собеседованиях в Google и других компаниях
Двадцать задачек (по безумной, восхитительной геометрии) / Хабр
Предупреждение врача.
Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
1. Сад часов
Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)
«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».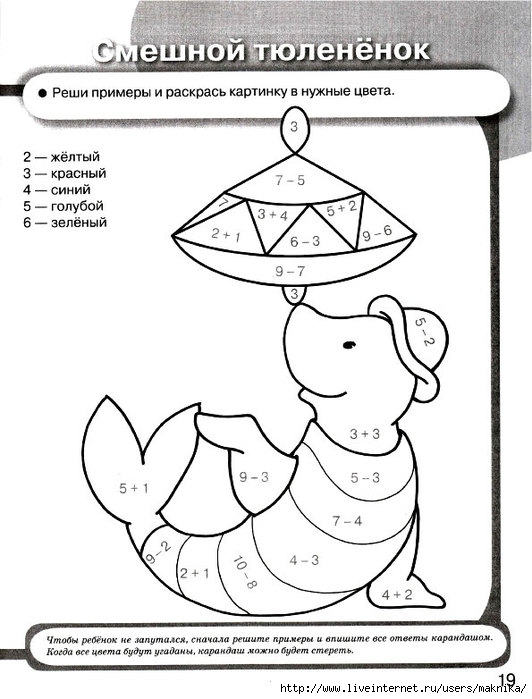
2. Опрокинутый квадрат
(Как по мне, это классика).
3. Это ловушка
В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?
«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».
4. Три квадратных тарелки
Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?
«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».
5. Красивая стрижка
Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?
«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».
6. Все люди рождены равными
«Ещё одна переделка, которую я предпочитаю оригиналу».
7. Полукруг турдакен
«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности.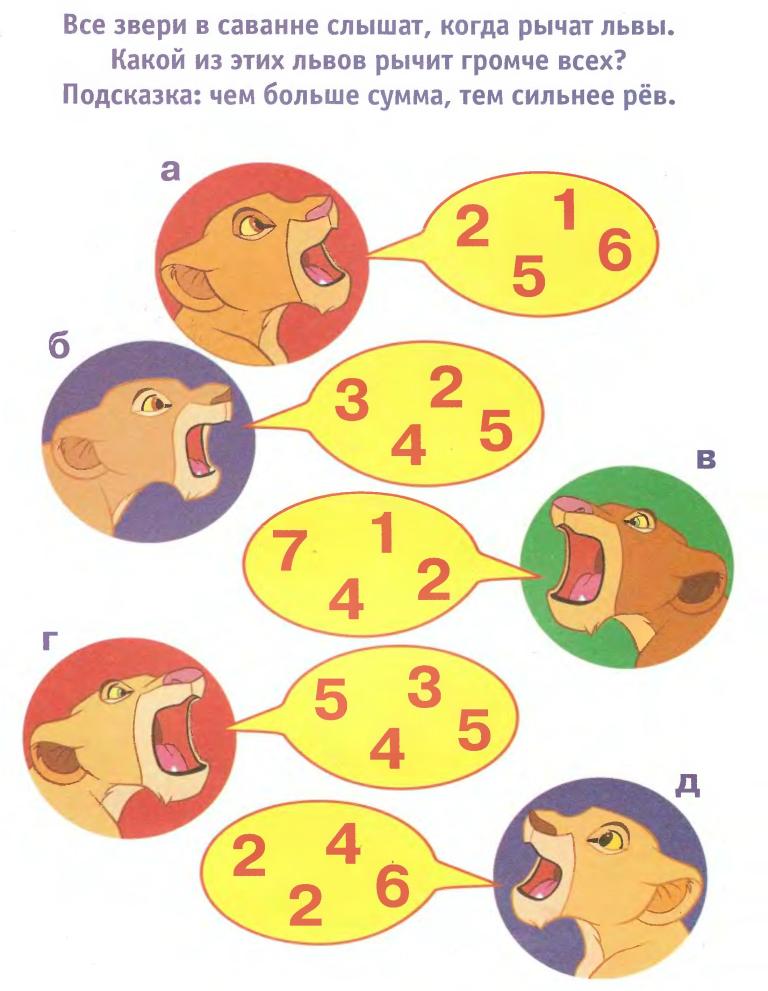
Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».
8. Степенные хорды
Какова площадь круга?
«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»
9. Сказка о двух кругах
У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.
«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»
10. Doc Oct
У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?
«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».
11. Всё в квадрате
«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».
12. Шип в улье
Два из правильных шестиугольников идентичны; у третьего площадь 10.
Какова площадь красного треугольника?
«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».
13. Я видел равнобедренных
Все четыре треугольника равнобедренные. Найдите угол.
«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»
14. Зеленый против синего
На картинке больше зелёного цвета или синего (и на сколько)?
«Ещё одна из моих любимых».
15. Резцы по камню
Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?
«Тут самое лучшее — действительно хорошие решения по рассечению площади».
16. Едем, едем, уехалиугольник
Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?
«Здесь ответ не такой красивый, но очень удивил меня.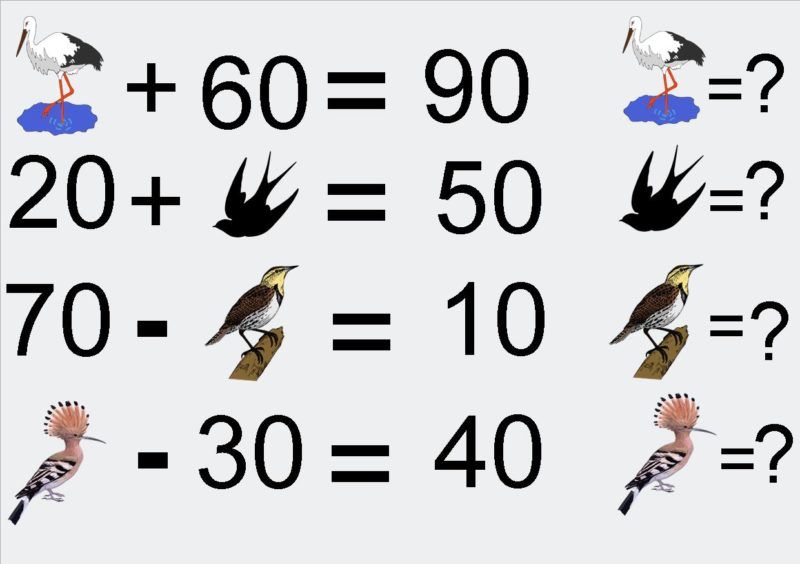
Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»
17. Только один факт
Какова площадь этого квадрата?
«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».
18. Стиральная машина
Какая часть большого квадрата закрашена?
«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».
19. Летающие флаги
У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?
«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».
20. Тигрогон
Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.
«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».
Закат над Квадратным городом
У левого квадрата площадь 4.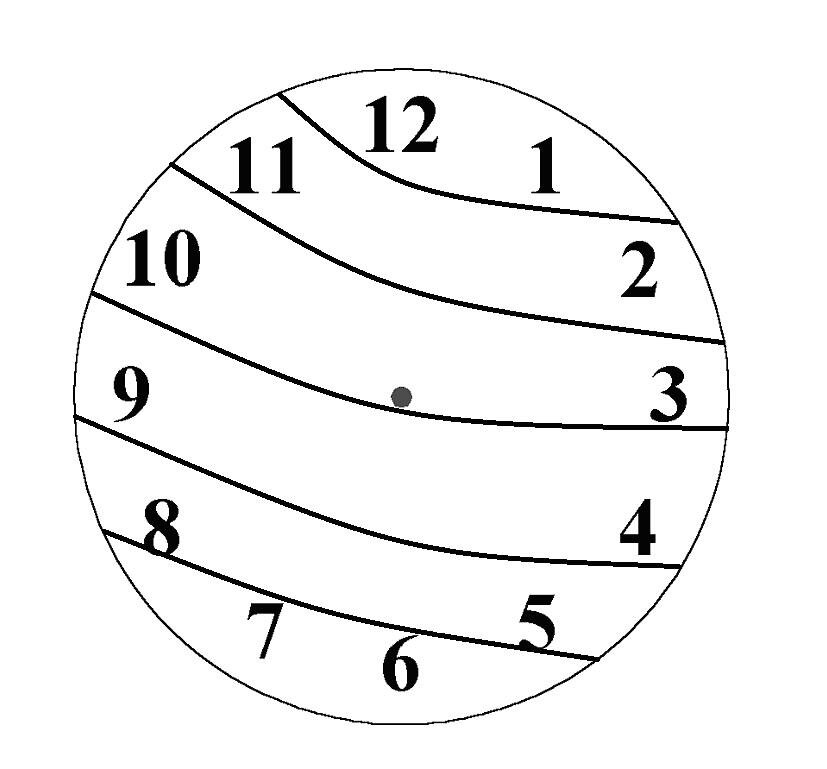
Какова площадь правого квадрата?
«Мне нравится эта задачка, она напоминает закат над городом скверов.”
Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.
Как вы пришли к разработке своих головоломок?
Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.
Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.
Как проходит творческий процесс?
Всё начинается с рисования бессмысленных фигурок.
В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.
Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?
Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.
Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.
Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.
Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?
Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!
Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!
Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.
Советы для потенциальных создателей головоломок?
Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.
Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:
- Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
- Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
- Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.
В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы.
Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.
Математические задачи от Good Will Hunting, с решениями | by Jørgen Veisdal
Фото : © 1997 Miramax Pictures
Цель этой статьи — рассказать вам о решениях двух математических задач, решенных вымышленным персонажем Уиллом в фильме 1997 года «Умница Уилл Хантинг», удостоенном премии «Оскар». Повествование в значительной степени основано на превосходной статье «Математика в охоте за доброй волей II: проблемы с точки зрения студентов » Хорвата, Коранди и Сабо (2010).
Музыка для настроения Spotify. Приятного чтения!
Краткое изложение Умница Уилл Хантинг рассказывает историю вымышленного персонажа Уилла Хантинга, который, несмотря на свой исключительный интеллект, работает уборщиком в Массачусетском технологическом институте в Бостоне. Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса.
Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно представляет свое решение на доске.
Когда на следующий день ни один из студентов Ламбо не претендует на зачет, профессор ставит другую, более сложную задачу. Уилл снова решает ее, но профессор ловит его в момент написания своего решения, который потрясен, узнав, что самый блестящий молодой математик в Массачусетском технологическом институте — необразованный уборщик.
Профессор Джеральд Ламбо (Стеллан Скарсгард) просматривает предложенное Уиллом решение. Фото : © 1997 Miramax Pictures
Задача 1: По графу G найти 1. Матрица смежности, A
2. Матрица, задающая количество 3-шаговых блужданий
3. Производящая функция для блужданий от i → j
4. Производящая функция для блужданий от 1 → 3
Рисунок 1: График G
Первая задача теории графов требует количества обходов от вершины i до вершины j в графе G.
Для этого пусть G — граф с множеством вершин V = {1, 2 , 3, 4} и множество ребер E = {(1,2), (1,4), (2,4), (2,3),(2,3)}, где (2,3) — обоюдоострый.
Решения задачи 1
Задача 1.1
Для заданного графа G найдите матрицу смежности A
Матрица смежности — это квадратная матрица, используемая для представления конечного графа. Элементы матрицы смежности L указывают, являются ли пары вершин в графе смежными или нет. Для простого графа с набором вершин V матрица смежности представляет собой квадрат |L| × |Л| матрица такая, что ее элемент L ᵢⱼ равен 1, когда есть одно ребро из вершины i до вершины j , 2, если их два, и ноль, если нет ребер из вершины i в вершину j. Все диагональные элементы матрицы равны нулю, так как ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль набора ребер E это дает нам следующую матрицу смежности для графа G:
Решение 1.
1. Реберные элементы от вершин i до j и матрица смежности графа G, показывающая количество ребер между вершинами i и j
Задача 1.2
Найдите матрицу, определяющую количество трехшаговых прогулок
Вторая задача в задаче 1 требует найти матрицу, которая кодирует все возможные прогулки длины 3 (Knill, 2003). То есть найти количество различных последовательностей ребер, соединяющих каждую отдельную последовательность вершин.
n + 1 шаг от i до j состоит из n шагов от i до k и затем 1 шаг от 9от 0005 к до j . То есть запись ij L ⁿ⁺¹ задается суммой:
Equation 1
Что на английском языке для этой задачи гласит, что «количество обходов длины 3 из вершины i в j» равно сумма «количества прогулок длины 2 от вершины i до k» , умноженная на «количество прогулок длины 1 от вершины k до j» для k = 1,2. Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу:
Решение 1.
2. Матрица, представляющая число 3 обходов из вершины i в j в графе G
Задача 1.3
Найти производящую функцию для обходов из i → j
В третьей задаче задачи 1 требуется найти производящую функцию из вершины i от до j . Чтобы ответить на этот вопрос, Хорват и др. (2010) рассматривают аналитическую производящую функцию, определяемую степенным рядом
Уравнение 2
Где коэффициент zⁿ обозначает число n шагов с i до j . Из задачи 1.3 мы нашли, что ω_n(i → j) является ij элементом матрицы Lⁿ . В задаче требуется производящая функция, которая дает все элементы одновременно, поэтому имеет смысл рассмотреть матрицу L , заданную знакомым степенным рядом (Horváth et al, 2010):
Уравнение 3
Где Lⁿ — это матрица, содержащая количество ступенчатых обходов от каждой вершины i до j (общий случай решения задачи 1.
2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда: Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
Уравнение 5
По правилу Крамера, если M обратима (существует некоторая n×n матрица N такая, что M × N = N × M = 007 6 I_n 900), то M × N 9000 Уравнение 6
То есть запись ij обратной матрицы M: 8
Замена M:
Решение 1.3. 9(i+j) (вероятно, из-за обозначений), и он обозначает единичную матрицу с 1 вместо более распространенного I .
Задача 1.4
Найти производящую функцию для блужданий от 1 → 3
Для решения задачи 1.4 просто применим общую формулу для блужданий от i к j (из задачи 1.3) к случаю блужданий от 1 → 3 :
Уравнение 9.
Определители которого найти несложно:
Уравнения 10 и 11. Определители ( I − zL ) и его младший/приведенный определитель ( I ₁₃ − zL ₁₃)
Задав следующие выражения, получим, используя определение определителя:
Уравнение 12. Формула для определения производящей функции для обходов из вершины 1 в вершину 3. Уравнение 003. Формула для определения значений производящей функции для блужданий из вершины 1 в вершину 3, решенная
Для получения коэффициентов этого степенного ряда вычисляется ряд Тейлора функции:
Уравнение 14. Функция для вычисления ряда Тейлора f(z) — ряд Маклорена, где fⁿ(0) — n-я производная от f при 0,
Для нашего выражения f(z) мы можем использовать правило частных, где g(z) = 2z² и h(z) = 4z³− 6z² −z +1. В фильме Уилл приводит значения первых шести производных разложения f(z):
Решение 1.4. Разложение Тейлора для определения значений производящей функции для блужданий из вершины 1 в вершину 3А потрясенный профессор Ламбо смотрит на правильное решение второй задачи, данное анонимным уборщиком, которого он только что прогнал.
Фото : © 1997 Miramax Pictures
Поскольку Уилл не расписался на доске за решение первой задачи, профессор Ламбо поставил вторую задачу, о которой он сообщает своему классу , что «нам потребовалось более двух лет, чтобы доказать» . Задача снова касается древовидных структур:
Задача 2
a. Сколько существует деревьев с n помеченными вершинами?
б. Нарисуйте все гомоморфно неприводимые деревья с n = 10
Решения задачи 2
Как указывают Horváth et al (2010), задача 2a на самом деле просто запрашивает формулу Кэли, которая для каждого положительного целого числа n количество деревьев на n -помеченных вершинах равно nⁿ⁻². Формула названа в честь Артура Кэли, но известна с тех пор, как была открыта Карлом Вильгельмом Борхардтом в 1860 году. учитывайте степени вершин, и поэтому с тех пор он носит его имя. Есть несколько известных доказательств результата.
Заключительное задание, задача 2б требует рисунков все гомоморфно неприводимые деревья с n = 10.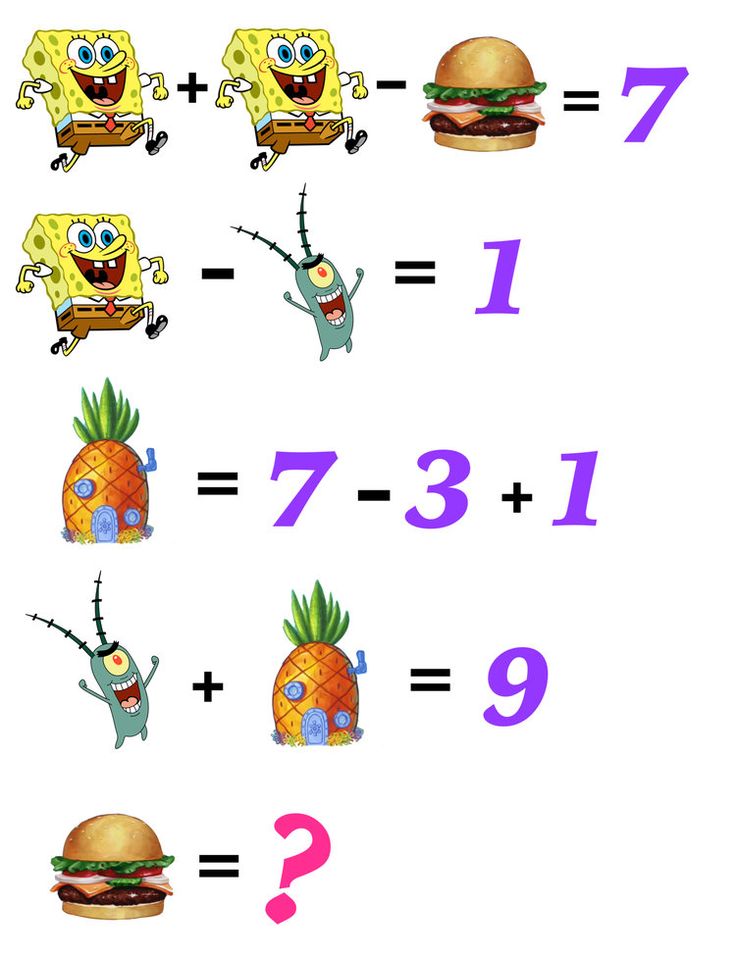
Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей «Число гомоморфно неприводимых деревьев и других видов » Харари и Принса ( 1959).
Мы можем сгруппировать гомоморфно неприводимые деревья, пометив их вершины цифрами 1,…., 10 и степени их вершин цифрами d₁, …,d₁₀ (Horváth et al, 2010). Поскольку у деревьев 10 вершин, мы знаем, что у них 9края. Мы можем классифицировать эти различные деревья по количеству их листьев (узлы/вершины степени вершины 1):
- Если есть 9 листьев и 1 нелист, то мы получаем «звезду», единственную вершину, соединенную с каждым листом :
- Если 8 листьев и 2 нелиста, то d₁ + d₂ = 10 и d₁ ≥ d₂ ≥ 3, поэтому либо: a) d₁ =7 и d₂ = 3 (одно дерево), или b ) d₁ = 6 и d₂ = 4 (одно дерево), или c) d₁ = d₂ = 5 (одно дерево).
Гомоморфно неприводимые деревья с 8 листьями
- Если листьев 7 , то d₁ + d₂ + d₃ = 11 и d₁ ≥ d₂ ≥d₃ ≥ 3, поэтому либо а) d₁ = d₂ = 5 и d₃ = 3 (два дерева), либо б) d₁ = 5 и d₂ = d₃ = 3 (три дерева).
